中序遍历二叉树全过程图解
文章目录
- 中序遍历图解
- 总结
- 拓展:回归与回溯
中序遍历图解

首先看下中序遍历的代码,其接受一个根结点root作为参数,判断根节点是否为nil,不为nil则先递归遍历左子树。
func traversal(root *TreeNode,res *[]int) {if root == nil {return}traversal(root.Left,res)*res = append(*res,root.Val)traversal(root.Right,res)
}
我们把树根结点A传递给它,其左结点为B,右结点为C。
首先我们要检查root是否为nil,其不为nil,通过递归继续遍历左边的子树,将左子树传递给递归函数,该层递归函数的root为B,其左子树为D 右子树为E,判断root是否为nil,root不为nil,继续将该树的左子树向下递归,该层递归函数的root为D,左右子树都为nil,我们检查root是否为nil,root为D,不为nil,继续递归遍历D的左子树,其左子树为nil,所以该层递归函数的root为nil,满足递归结束条件,执行return退出该层递归函数。
递到此处时的运行栈如下图所示

此时的return会回到root为D的递归层,D的左子树已经遍历完毕,我们执行下一行语句append,
该语句会将root的数据域加入到结构列表res中,即访问到了D,如下图

按照顺序继续执行,接下来将使用递归遍历D的右子树,这里D的右子树为nil,所以我们传入的递归参数也为nil,检测到root为nil,我们退出该层递归函数,回到调用层D,该层的所有语句都执行完毕了。我们继续回到调用它的函数,即B层的 traversal(root.Left,res)语句处

继续执行后序语句,执行 *res = append(*res,root.Val)记录root的数据域,即访问B,再执行下一条语句
递归访问B的右子树,将E传递给它,判断root是否为nil,root为E,不为nil,递归调用E的左子树,左子树为nil,判断root是否为nil,为nil,退出该层

执行下一行,将E记录到结果中,继续遍历E的右子树,右子树为nil,直接退出该层递归函数,返回到了E的递归层,E这层也执行完毕了,返回到调用它的B层

随即B层也执行完了,返回到调用它的A层 ,在该层执行下一行代码,将A记录到结果中,继续遍历A的右子树,A的右子树为C,其不为nil,递归C的左子树F,F不为nil,递归F的左子树,F的左子树为nil,即传入的root为nil,满足递归结束条件,开始回归上层。

返回到调用它的F层,将F记录到结果中。遍历F的右子树,F的右子树也为nil,退出该层,到此F这层函数执行完毕,返回到调用F的递归层 C,下一行语句记录C

继续下一行语句,递归C的右子树G,判断该层递归的root是否为nil,当前root为G,不为nil,递归G的左子树,左子树为nil,满足递归结束条件,返回到调用它的G,输出G,递归G的右子树,右子树为nil
满足递归结束条件,返回到调用它的G,G这层函数结束,返回上层到C
C也运行完毕,返回上层到A,A也运行完毕,此该树递归结束,这样我们就得到了中序遍历序列
总结
再次回顾一下代码
func traversal(root *TreeNode,res *[]int) {if root == nil {return}traversal(root.Left,res)*res = append(*res,root.Val)traversal(root.Right,res)
}
从我们的遍历全流程图解来看,不难理解,每个节点都是将其左子树全部递归遍历完后,才开始遍历其右子树的,如根节点A,是将其左子树BDE全部遍历完后,才开始遍历右子树的,注意思考递归栈哦,这样才能真正的理解。
中序遍历理解后,前序和后续遍历是一样的道理。这时一起看下后续遍历的代码:
func traversal(root *TreeNode,res *[]int) {if root == nil {return}traversal(root.Left,res)traversal(root.Right,res)*res = append(*res,root.Val)
}
很多同学看到递归左右子树的那两行代码,很容易陷入误区,以为那两行是"同时"在执行,认为遍历完root的左节点后,立马遍历了其右节点,这种理解是非常不对的,实际是遍历完整个左子树后,经过
归回到当前层,此时才会开始执行当前层的traversal(root.Right,res)语句去遍历右子树。
尤其是看到两条回溯语句写在同一行时会更容易误解,如力扣104. 二叉树的最大深度
/*** definition for a binary tree node.* type treenode struct {* val int* left *treenode* right *treenode* }*/
func max (a, b int) int {if a > b {return a}return b
}// 递归
func maxdepth(root *treenode) int {if root == nil {return 0}return max(maxdepth(root.left), maxdepth(root.right)) + 1
}
实际最后一行代码是简化版,等价于如下代码
/*** definition for a binary tree node.* type treenode struct {* val int* left *treenode* right *treenode* }*/
func max (a, b int) int {if a > b {return a}return b
}// 递归
func maxdepth(root *treenode) int {if root == nil {return 0}leftDepth := maxdepth(root.left) // 递归左子树的深度rightDepth := maxdepth(root.right) // 递归右子树的深度return max(leftDepth,rightDepth ) + 1 // 当前根节点到叶子节点的最大深度
}
此时再看此代码是不是好理解一些 ,它就是我们的后序遍历哇!将左子树全部遍历完后,才会开始遍历右子树,最后则是根节点,然后回到上层调用栈,直到所有接地那遍历完毕,递归函数执行完毕。
拓展:回归与回溯
这里就是一个简介,详细可见:LeetCode 257. 二叉树的所有路径(回溯详解)
前序遍历以及回溯的过程如图:
回溯和递归中回归的区别:
回溯:因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
回归:下层函数栈执行完成后,回归到上层函数栈来实际上,回溯和回归都是伴随递归出现的,
只是回溯比回归多了一个路径回退的操作。

相关文章:

中序遍历二叉树全过程图解
文章目录 中序遍历图解总结拓展:回归与回溯 中序遍历图解 首先看下中序遍历的代码,其接受一个根结点root作为参数,判断根节点是否为nil,不为nil则先递归遍历左子树。 func traversal(root *TreeNode,res *[]int) {if root nil …...
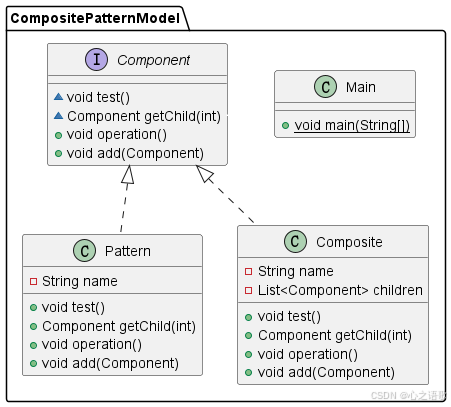
设计模式 组合模式(Composite Pattern)
组合模式简绍 组合模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树形结构来表示“部分-整体”的层次结构。组合模式使得客户端可以用一致的方式处理单个对象和组合对象。这样,可以在不知道对象具体类型的条…...

在vue中嵌入vitepress,基于markdown文件生成静态网页从而嵌入社团周报系统的一些想法和思路
什么是vitepress vitepress是一种将markdown文件渲染成静态网页的技术 其使用仅需几行命令即可 //在根目录安装vitepress npm add -D vitepress //初始化vitepress,添加相关配置文件,选择主题,描述,框架等 npx vitepress init //…...
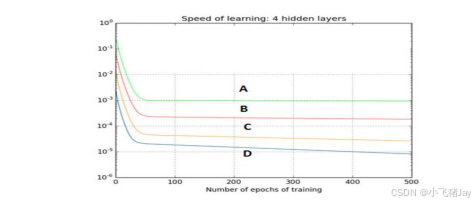
神经网络面试题目
1. 批规范化(Batch Normalization)的好处都有啥?、 A. 让每一层的输入的范围都大致固定 B. 它将权重的归一化平均值和标准差 C. 它是一种非常有效的反向传播(BP)方法 D. 这些均不是 正确答案是:A 解析: batch normalization 就…...

C语言题目之单身狗2
文章目录 一、题目二、思路三、代码实现 提示:以下是本篇文章正文内容,下面案例可供参考 一、题目 二、思路 第一步 在c语言题目之打印单身狗我们已经讲解了在一组数据中出现一个单身狗的情况,而本道题是出现两个单身狗的情况。根据一个数…...
)
Vue2学习笔记(03关于VueComponent)
1.school组件本质是一个名为Vuecomponent的构造函数,且不是程序员定义的,是Vue.extend生成的。 2.我们只需要写<school/>或<school></school>,Vue解析时会帮我们创建school组件的实例对象,即Vue帮我们执行的:new Vuecompo…...

微服务架构中常用技术框架
认证授权 Spring Security OAuth 2.0 JWT Keycloak Istio Apache Shiro 日志监控 ELK Prometheus Grafana Fluentd CI/CD Jenkins GitLab CI CircleCI ArgoCD 服务通信 gRPC REST API Apache Thrift Apache Avro Apache Dubbo OpenFegin 断路器 Hystr…...
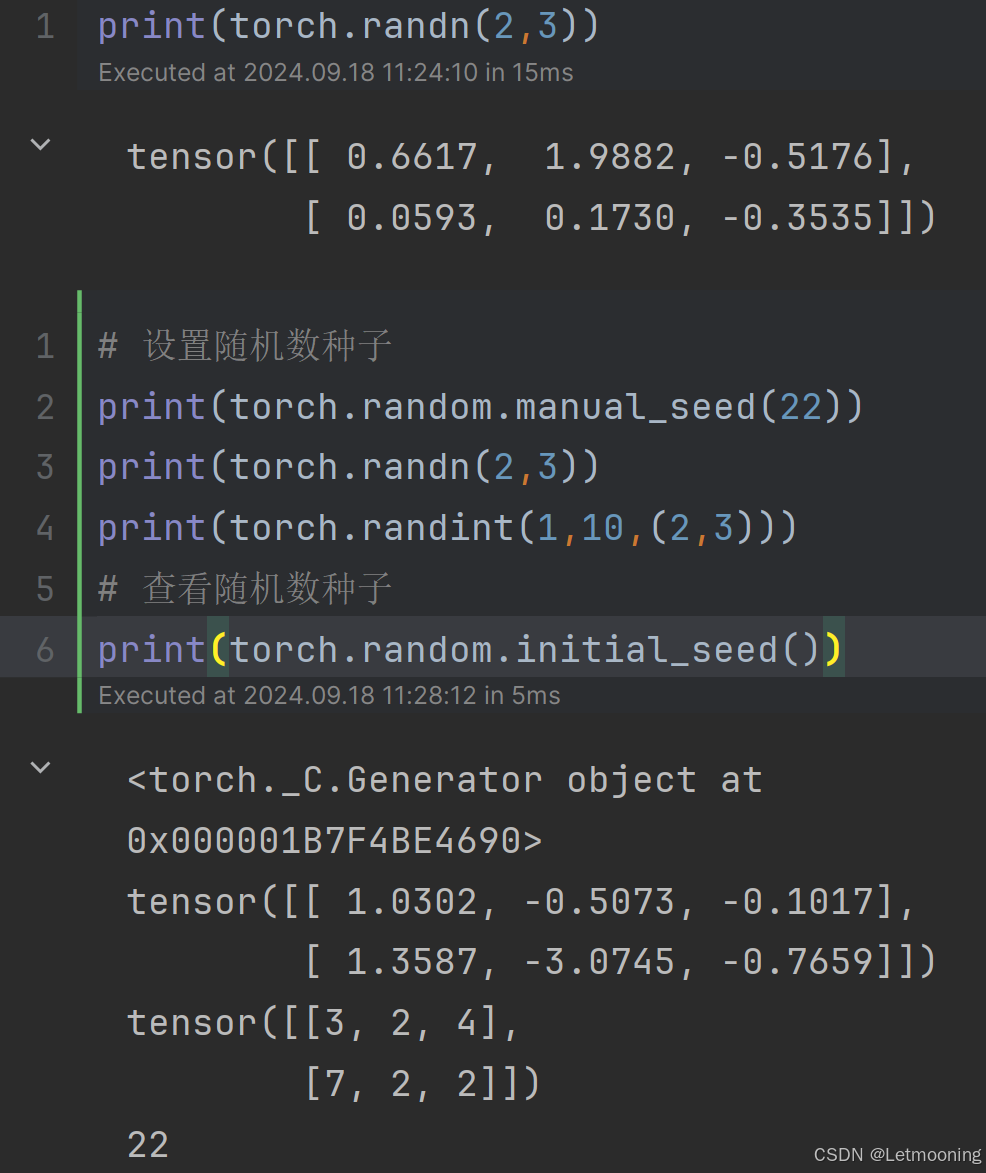
[深度学习]Pytorch框架
1 深度学习简介 应用领域:语音交互、文本处理、计算机视觉、深度学习、人机交互、知识图谱、分析处理、问题求解2 发展历史 1956年人工智能元年2016年国内开始关注深度学习2017年出现Transformer框架2018年Bert和GPT出现2022年,chatGPT出现,进入AIGC发展阶段3 PyTorch框架简…...

华为HarmonyOS灵活高效的消息推送服务(Push Kit) - 5 发送通知消息
场景介绍 通知消息通过Push Kit通道直接下发,可在终端设备的通知中心、锁屏、横幅等展示,用户点击后拉起应用。您可以通过设置通知消息样式来吸引用户。 开通权益 Push Kit根据消息内容,将通知消息分类为服务与通讯、资讯营销两大类别&…...
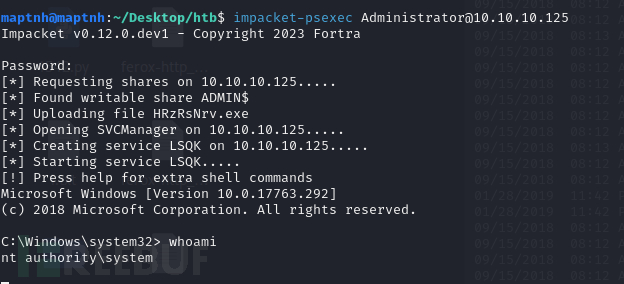
[Meachines] [Medium] Querier XLSM宏+MSSQL NTLM哈希窃取(xp_dirtree)+GPP凭据泄露
信息收集 IP AddressOpening Ports10.10.10.125TCP:135, 139, 445, 1433, 5985, 47001, 49664, 49665, 49666, 49667, 49668, 49669, 49670, 49671 $ nmap -p- 10.10.10.125 --min-rate 1000 -sC -sV -Pn PORT STATE SERVICE VERSION 135/tcp open msrp…...

新版ssh客户端无法连接旧版服务器sshd的方法
新安装完的windows 版本,连Linux服务器直接报错 C:\Users\wang>ssh root192.168.110.50 Unable to negotiate with 192.168.110.50 port 22: no matching key exchange method found. Their offer: diffie-hellman-group14-sha1,diffie-hellman-group1-sha1,kex…...
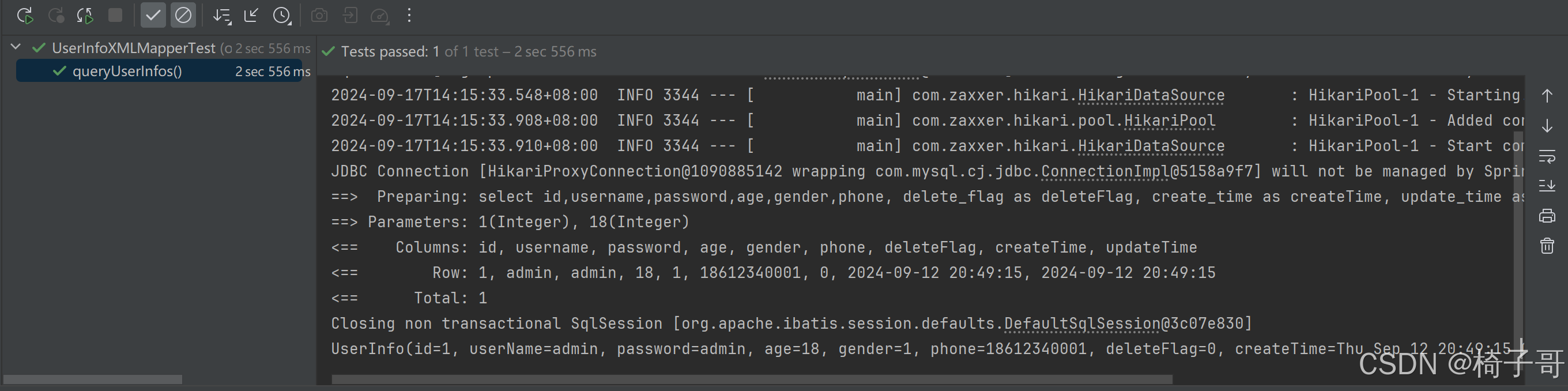
MyBatis操作数据库-XML实现
目录 1.MyBatis的简单介绍 2.MyBatis操作数据库的步骤 2.1 添加依赖 2.2 配置文件 2.3 写持久层代码 2.4 方法测试 3.MyBatis操作数据库(增删查改) 3.1 CRUD标签 3.2 参数传递 3.3 Insert-新增 3.4 Delete-删除 3.5 Update-修改 3.6 Select-查询(映射问题) 1.MyB…...
华为HarmonyOS地图服务 5 - 利用UI控件和手势进行地图交互
场景介绍 本章节将向您介绍如何使用地图的手势。 Map Kit提供了多种手势供用户与地图之间进行交互,如缩放、滚动、旋转和倾斜。这些手势默认开启,如果想要关闭某些手势,可以通过MapComponentController类提供的接口来控制手势的开关。 接口…...
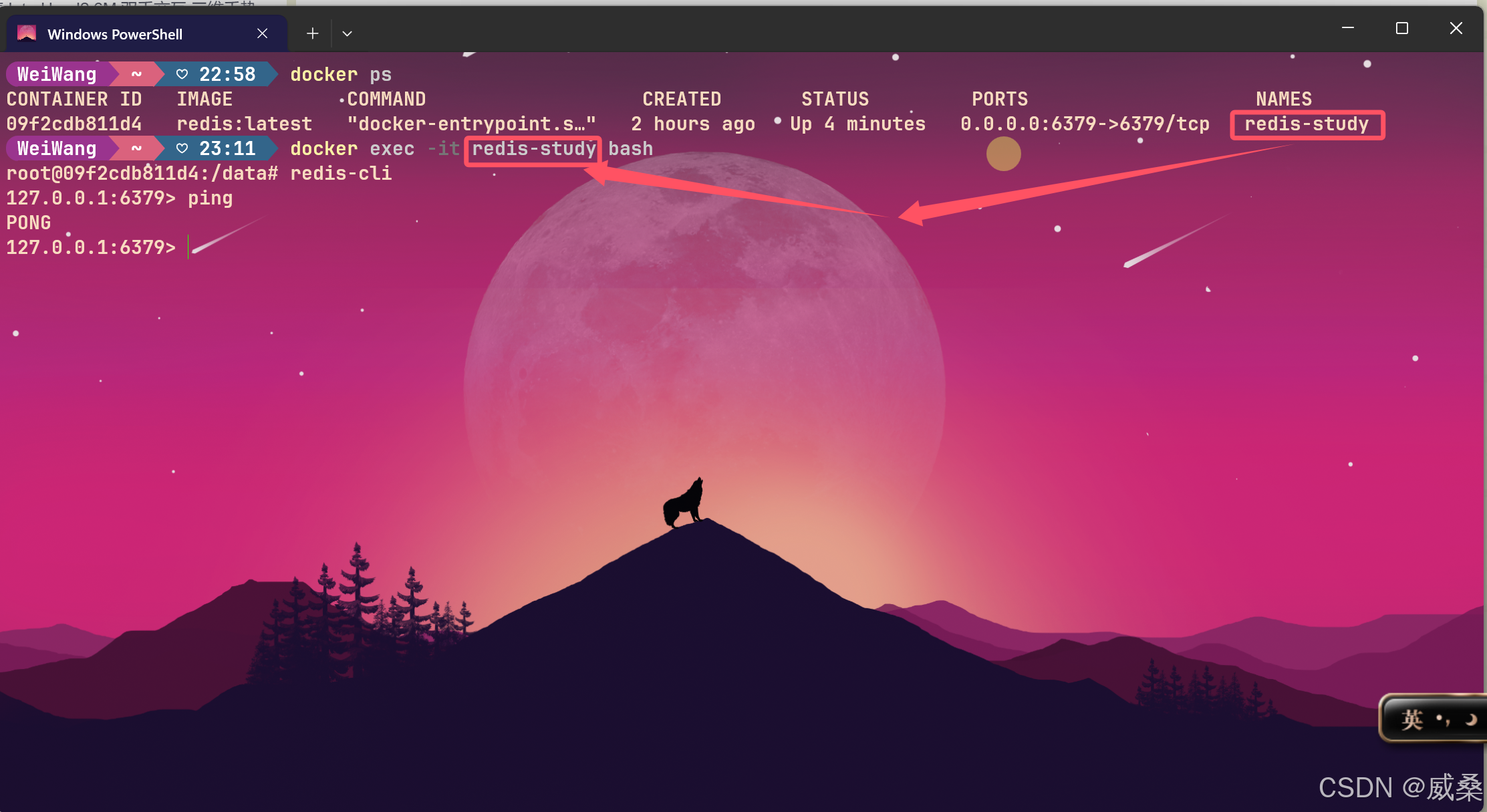
解决DockerDesktop启动redis后采用PowerShell终端操作
如图: 在启动redis容器后,会计入以下界面 : 在进入执行界面后如图: 是否会觉得界面过于单调,于是想到使用PowerShell来操作。 步骤如下: 这样就能使用PowerShell愉快地敲命令了(颜值是第一生…...

react + antDesign封装图片预览组件(支持多张图片)
需求场景:最近在开发后台系统时经常遇到图片预览问题,如果一个一个的引用antDesign的图片预览组件就有点繁琐了,于是在antDesign图片预览组件的基础上二次封装了一下,避免重复无用代码的出现 效果 公共预览组件代码 import React…...
比较)
逻辑回归 和 支持向量机(SVM)比较
为了更好地理解为什么在二分类问题中使用 SVM,逻辑回归的区别,我们需要深入了解这两种算法的区别、优势、劣势,以及它们适用于不同场景的原因。 逻辑回归和 SVM 的比较 1. 模型的核心思想 • 逻辑回归: • 基于概率的模型&…...

GS-SLAM论文阅读笔记--TAMBRIDGE
前言 本文提出了一个自己的分类方法,传统的视觉SLAM通常使用以帧为中心的跟踪方法,但是3DGS作为一种高效的地图表达方法好像更侧重于地图的创建。这两种方法都有各自的优缺点,但是如果能取长补短,互相结合,那么就会是…...

[Redis面试高频] - zset的底层数据结构
文章目录 [Redis面试高频] - zset的底层数据结构一、引言二、zset 的底层数据结构1、zset 的编码方式1.1、ziplist 编码1.2、skiplist 编码 1.3、ziplist 编码适用条件1.4、skiplist 编码适用条件2、zset 的操作命令 三、zset 的性能考量1、内存效率2、搜索效率 四、总结 [Redi…...

搜维尔科技:OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作
OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作 搜维尔科技:OptiTrack将捕捉到的人类动作数据映射到人形机器人的各个关节上进行遥操作...

CentOS Linux教程(6)--CentOS目录
文章目录 1. 根目录2. cd目录切换命令3. CentOS目录介绍4. pwd命令介绍5. ls命令介绍5.1 ls5.2 ls -a5.3 ls -l 1. 根目录 Windows电脑的根目录是计算机(我的电脑),然后C盘、D盘。 Linux系统的根目录是/,我们可以使用cd /进入根目录,然后使…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
