【砝码称重】暴力DFS(一半分)+ dp(可AC)
题目描述:
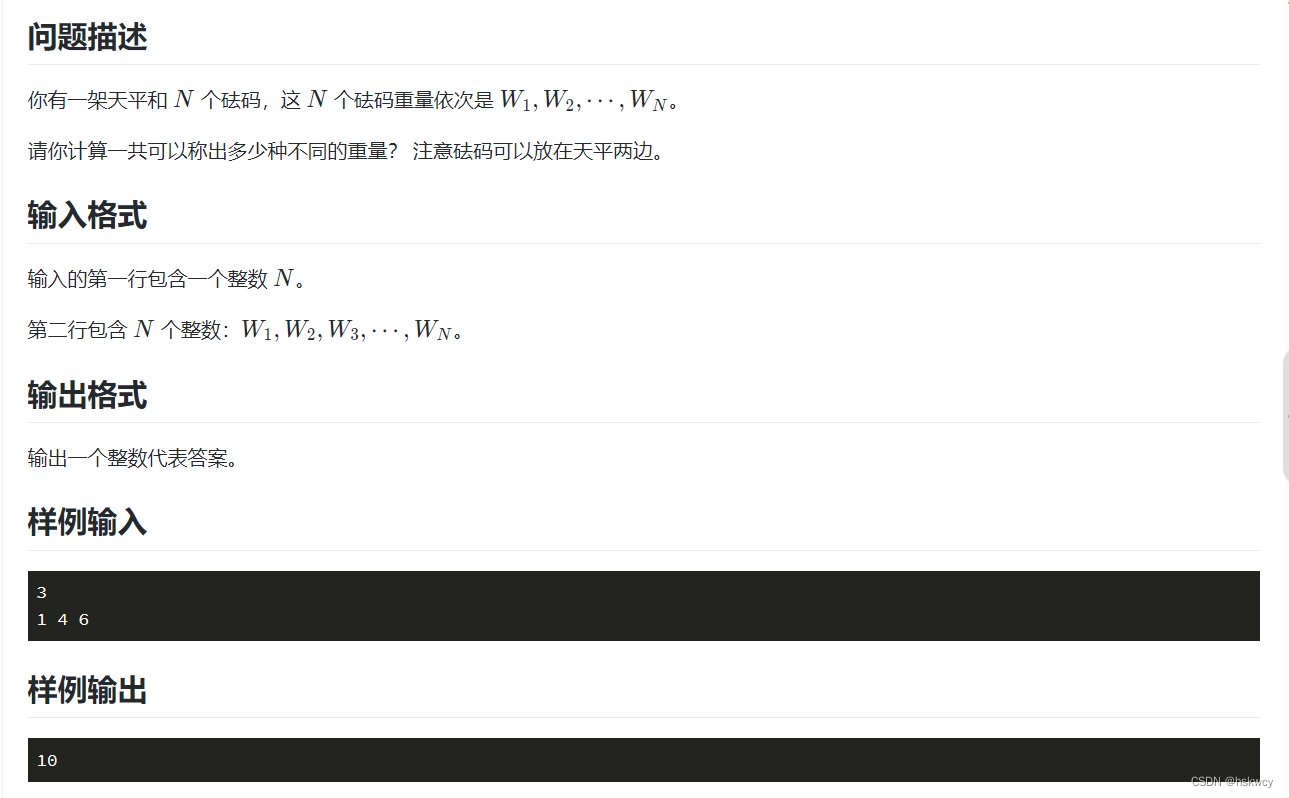
题目分析:

我也没有完全搞太明白,简单说说我的理解
1.dp【i】【j】表示前 i 个砝码,是否可以称出来重量为 j 的物品,如果可以的话,值为1,不可以
为0;
2.针对当前第 i 个砝码,一共有三种选择,分别是放到左边、右边又或者是不放该砝码【优先将砝码放在右边】
如题例所示:第一个砝码【重 1】可以称重 0 与 1 两个重量
此时开始处理第二个砝码,重 4 :
第一种:将砝码放在右边:那么右边砝码的重量就是 1 + 4 = 5;可以称出质量为 5 的物品,则dp【2】【5】= 1;
第二种:将砝码放在左边:那么右边砝码的重量就是 1 ,左边砝码质量为 4 ,可以称出质量为 3 的物品,则dp【2】【3】= 1;
第三种:不放砝码:可以称出质量为 1 的物品,则dp【2】【1】= 1;
但是如何用动态规划的思路将再这种思想用编程实现了:
首先,设定初始值当 0 个砝码时,只有 重量 0 可以被称出来,令dp【0】【0】= 1;其余值全部为0;
接下来:处理第一个砝码,依次判断dp【1】【j】的值,那怎么判断呢?
根据状态转移式: dp[i][j] = max(dp[i-1][j],max(dp[i-1][j+w[i]],dp[i-1][abs(j-w[i])]));
首先是dp【1】【0】= max(dp[0][0],max(dp[0][1],dp[0][1])) = 1;
解释:dp[0][0]:既然不放第 1 个物品,质量 0 就被称出来了,那么加上砝码 1 也可以称出来质量 0 ;dp[0][1]、dp[0][1]:表示前0个砝码的组合是否可以称出质量为4的物品。那肯定不可以,所以表达式dp【1】【0】的值就是1,表示前1个砝码可以称出体积为 0 的物品;
接下来判断dp【1】【1】:前前1个砝码可以称出体积为 1 的物品
dp【1】【1】= max(dp[0][1],max(dp[0][2],dp[0][0]))
解释:dp[0][1] = 0、dp[0][2] = 0【这个式子表示将第一个砝码放在右边的情况:只要这个dp[0][2] =1,说明可以称出来质量为2的物品,那么就能dp[1][1]也一定能成功,因为将该砝码放到左边,为了保持平衡,左边要再添加重量为 1 的物品,这样也就被称出来了】意思好像是:加在右边的话,是通过左边加物品实现平衡的
dp[0][0] = 1;【表示将砝码放在左边的情况】
再举个例子dp【3】【7】:
dp【2】【7】:
dp【2】【7 + 6】:如果为真,那就说明前两个砝码可以称出质量为13的物品,那么把该砝码放到天平左侧,为了保持平衡,左侧还需要添加质量为7的物品,那么质量为7的物品就被测量出来了
dp【2】【7 - 6】:如果为真,那就说明前两个砝码可以称出质量为1的物品,那么把该砝码放到天平右侧,为了保持平衡,左侧还需要添加质量为7的物品,那么质量为7的物品就被测量出来了
题解代码:
dsp:
//砝码称重--一半的分
#include <bits/stdc++.h>
using namespace std;
const int vinf = 1e5+100; //砝码之和最大
int vis[vinf]; //用来标记该质量是否可以被称重
int n;
int val[vinf];
void dfs(int x,int y)
{if(y==n+1){if(x>=0){vis[x]=1;cout<<x<<endl;} return;}//开始深搜dfs(x + val[y],y + 1); // 砝码放到左边 dfs(x - val[y],y + 1); //砝码放到右边 dfs(x,y+1);
}
int main(){cin>>n;//输入砝码的重量for(int i=1;i<=n;++i){//cin>>val[i]; //打印出可以撑出来的 }//已经读取了砝码的重量dfs(0,0); //初始状态左边为已经平衡的天平左边的重量,右边为第 i 个砝码//开始枚举每一个重量int ans = 0; for(int i=1;i<vinf;++i){if(vis[i]) ans++; }cout<<endl<<ans<<endl;return 0;
}dp:
//砝码称重--dp
#include <bits/stdc++.h>
using namespace std;
int n,w[110];
int dp[110][100005];
int ans = 0;
int main(){cin>>n;int sum=0;for(int i=1;i<=n;++i){cin>>w[i];sum+=w[i];}dp[0][0]=1;for(int i=1;i<=n;++i){for(int j=0;j<=sum;++j){dp[i][j] = max(dp[i-1][j],max(dp[i-1][j+w[i]],dp[i-1][abs(j-w[i])]));}}for(int i=1;i<=sum;++i){if(dp[n][i])ans++;}cout<<ans<<endl; return 0;
}相关文章:

【砝码称重】暴力DFS(一半分)+ dp(可AC)
题目描述: 题目分析: 我也没有完全搞太明白,简单说说我的理解 1.dp【i】【j】表示前 i 个砝码,是否可以称出来重量为 j 的物品,如果可以的话,值为1,不可以 为0; 2.针对当前第 i 个…...
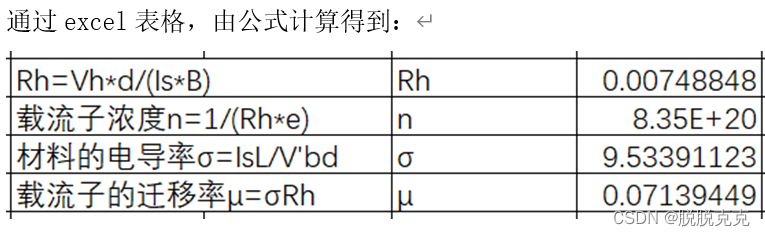
科大奥瑞物理实验——霍尔效应实验
实验名称:霍尔效应实验 1. 实验目的: 了解霍尔效应测量磁场的原理和方法;观察磁电效应现象;学会用霍尔元件测量磁场及元件参数的基本方法。 2. 实验器材: QS-H型霍尔效应实验仪 磁针 QS-H型霍尔效应测试仪 双刀开关…...
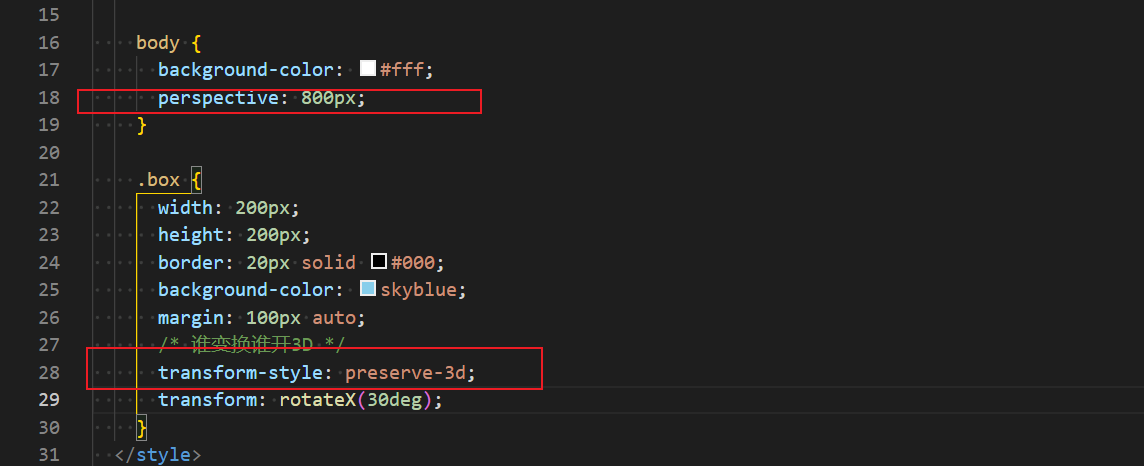
2023_深入学习HTML5
H5 基于html5和 css3和一部分JS API 结合的开发平台(环境) 语义化标签 header : 表示头部,块级元素 footer : 表示底部,块级元素 section :区块 nav : 表示导航链接 aside : 表示侧边栏 output &am…...
Apache iotdb-web-workbench 认证绕过漏洞(CVE-2023-24829)
漏洞简介 影响版本 0.13.0 < 漏洞版本 < 0.13.3 漏洞主要来自于 iotdb-web-workbench IoTDB-Workbench是IoTDB的可视化管理工具,可对IoTDB的数据进行增删改查、权限控制等,简化IoTDB的使用及学习成本。iotdb-web-workbench 中存在不正…...

【7-1】Redis急速入门与复习
文章目录1、分布式架构概述本阶段规划什么是分布式架构单体架构与分布式架构 对比分布式架构优点分布式架构缺点设计原则2、为何引入Redis现有架构的弊端3、什么是NoSql?NoSqlNoSql优点NoSql常见分类4、什么是分布式缓存,什么是Redis?什么是分…...
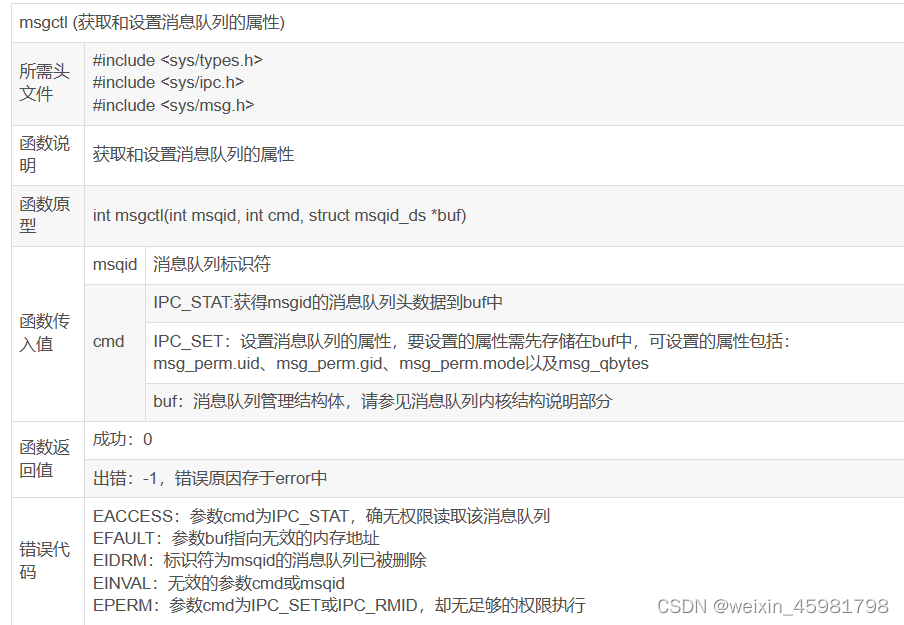
5、操作系统——进程间通信(3)(system V-IPC:消息队列)
目录 1、管道的缺点 2、消息队列 3、消息队列的API (1)获取消息队列的ID(类似文件的描述符)(msgget) (2)发送、接收消息(msgrcv) (3)获取和设置消息队列的属性(msgctl) 4、消息队…...
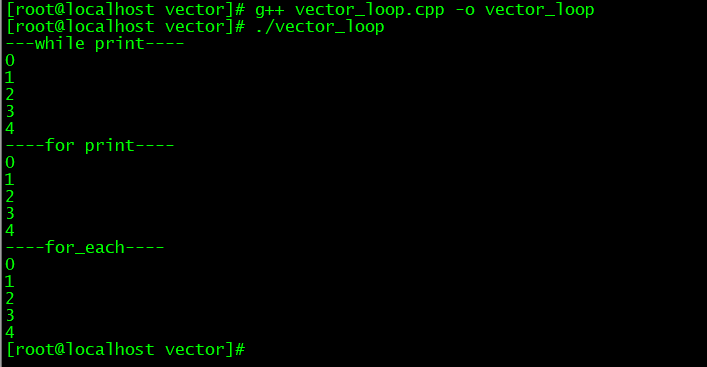
C++vector容器用法详解
一、前言vector 是封装动态数组的顺序容器,连续存储数据,所以我们不仅可以通过迭代器访问存储在 vector 容器中的数据,还能用指向 vector 容器中的数据的常规指针访问数据。这意味着指向 vector 容器中的数据的指针能传递给任何期待指向数组元…...

Log4j2的Loggers详解
引言 官方配置文档:https://logging.apache.org/log4j/2.x/manual/filters.html Loggers节点 Loggers节点常见的有两种:Root和Logger <Loggers><Logger name"org.apache.logging.log4j.core.appender.db" level"debug" additivity&qu…...

计算机视觉的应用1-OCR分栏识别:两栏识别三栏识别都可以,本地部署完美拼接
大家好,我是微学AI,今天给大家带来OCR的分栏识别。 一、文本分栏的问题 在OCR识别过程中,遇到文字是两个分栏的情况确实是一个比较常见的问题。通常情况下,OCR引擎会将文本按照从左到右,从上到下的顺序一行一行地识别…...

低代码平台如何选型, 43款国内外低代码平台一网打尽
目前,零代码技术和低代码技术越来越成熟,低代码平台也越来越被大家所接受,国内低代码平台厂商和产品层出不穷,到底哪家低代码平台好,企业如何选型,以下给出一些参考。 一、低代码平台如何选型 企业如何选…...
第六周作业(1.5小时)
一、PreparedStatement PreparedStatement也可以用来执行sql语句,但是需要注意:它需要用sql创建好PreparedStatement,而Statement不需要用sql来创建。 优点: 1、具有较好的可维护性和可读性,参数的分别插入减少了错…...

排序 (蓝桥杯) JAVA
目录题目描述:冒泡排序算法(排序数字,字符):String与String buffer的区别:纯暴力破解(T到爆炸):暴力破解加思考(bingo):总结:题目描述: 小蓝最近学习了一些排序算法,其中冒泡排序让他…...

【Blender 水墨材质】实现过程剖析01
写在前面 想把Blender一位大佬演示的Blender水墨材质过程,在Unity用Shader重现,过程中会拿能拿到的节点代码举例(ShaderGraph或者UE的都会有)。第一步当然是要跟着人家做一遍!我会尽可能地分析一下每一步的原理~ 教程…...

代码随想录算法训练营第五十六天|583. 两个字符串的删除操作、72. 编辑距离
LeetCode 583 两个字符串的删除操作 题目链接:https://leetcode.cn/problems/delete-operation-for-two-strings/ 思路: 方法一:两个子串同时删除元素 dp数组的含义 dp[i][j]dp[i][j]dp[i][j]代表以i-1为结尾的字符串word1,和以j-1位结…...
【ArchLinux】【KDE】Archlinux的安装与使用
文章目录开头前言所需环境演示环境相关链接安装教程在Windows环境下制作启动盘进入ArchLinux Live环境安装为硬盘分区如何新建分区?分区表格式化分区分区完成,开始安装挂载分区切换镜像源安装基本系统设置将Live环境(当前)挂载信息…...

Go语言精修(尚硅谷笔记)第六章
六、函数、包和错误处理 6.1 函数概念 不用函数的弊端 1)写法可以完成功能, 但是代码冗余 2 ) 同时不利于代码维护 概念:为完成某一功能的程序指令(语句)的集合,称为函数。 在Go中,函数分为: 自定义函数、系统函数 基本语法 //函数的基本语法 fu…...

Photoshop的功能
Photoshop是一款功能强大的图片编辑软件,它提供了数百种不同的工具和特效,让您可以编辑图片、创建图形和设计网页等。 以下是Photoshop的一些主要功能: 1.图层:Photoshop允许您创建多个图层,让您可以在每一个图层上进…...

C++初阶——内存管理
目录 1. C/C内存分布 2. C语言中动态内存管理方式:malloc/calloc/realloc/free 3. C内存管理方式 3.1 new/delete操作内置类型 3.2 new和delete操作自定义类型 4. operator new与operator delete函数 重要 4.1 operator new与operator delete函数(…...
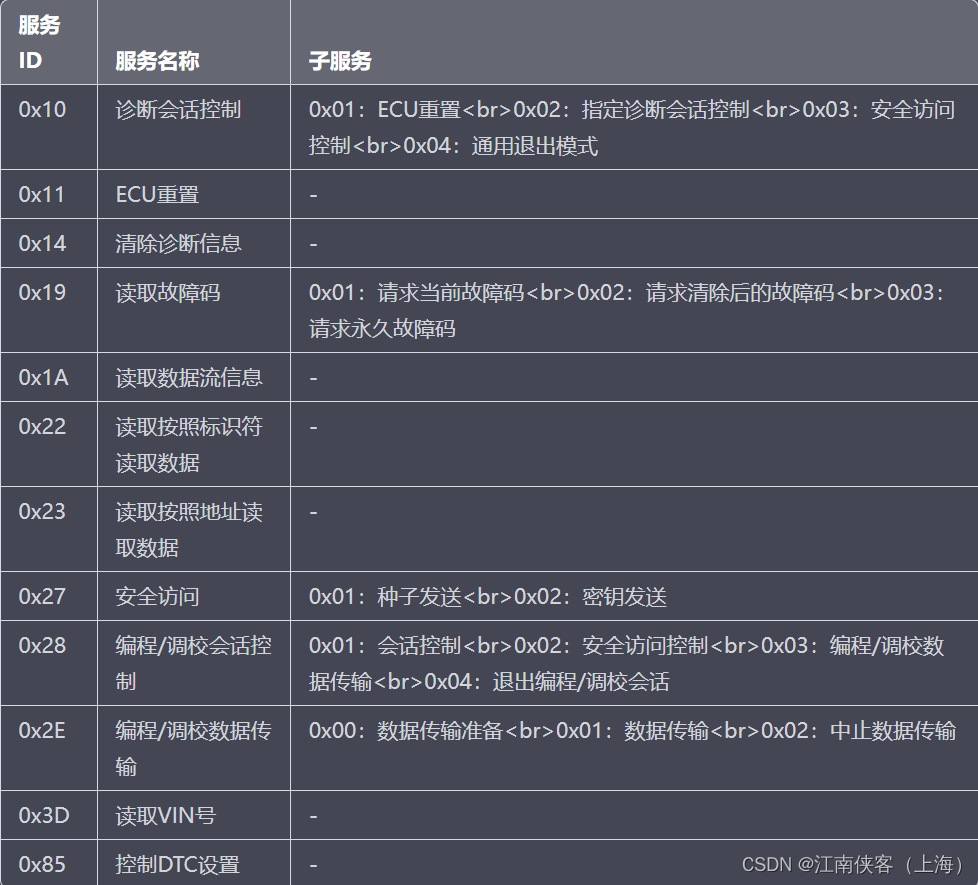
uds服务汇总
还有一些服务列举在下面: RequestDownload(服务ID为0x34)和RequestUpload(服务ID为0x35):这两个服务用于在ECU和诊断器之间进行数据传输。通过 RequestDownload服务,诊断器可以请求ECU接收一些数…...

【深度学习】2023李宏毅homework1作业一代码详解
研一刚入门深度学习的小白一枚,想记录自己学习代码的经过,理解每行代码的意思,这样整理方便日后复习也方便理清自己的思路。感觉每天时间都不够用了!!加油啦。 第一部分:导入模块 导入各个模块࿰…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
