微信小程序操作蓝牙
主要流程:
1.初始化蓝牙适配器openBluetoothAdapter,如果不成功就onBluetoothAdapterStateChange监听蓝牙适配器状态变化事件
2.startBluetoothDevicesDiscovery开始搜寻附近的蓝牙外围设备
3.onBluetoothDeviceFound监听寻找到新设备的事件,可以用代码匹配设备
4 .createBLEConnection创建蓝牙连接,顺便在stopBluetoothDevicesDiscovery关闭搜寻附近的蓝牙外围设备
注意:由于系统限制,Android 上获取到的 deviceId 为设备 MAC 地址,iOS 上则为设备 uuid。
5.getBLEDeviceServices获取蓝牙设备所有服务
6.getBLEDeviceCharacteristics获取蓝牙设备某个服务中所有特征值
7.onBLECharacteristicValueChange监听蓝牙设备发送给你的数据
8.writeBLECharacteristicValue向蓝牙设备发送一个0x00的16进制数据或者writeBLECharacteristicValueString发送字符串

相关文章:

微信小程序操作蓝牙
主要流程: 1.初始化蓝牙适配器openBluetoothAdapter,如果不成功就onBluetoothAdapterStateChange监听蓝牙适配器状态变化事件 2.startBluetoothDevicesDiscovery开始搜寻附近的蓝牙外围设备 3.onBluetoothDeviceFound监听寻找到新设备的事件,…...

Python爱心射线(完整代码)
目录 系列目录 写在前面 完整代码 下载代码 代码分析 写在后面 系列目录 序号直达链接表白系列1Python制作一个无法拒绝的表白界面2Python满屏飘字表白代码3...

努比亚 Z17 NX563J Root 教程三方REC刷写工具教程
教程:1,自用成功 正常链接列表 adb devices 检查fastboot链接列表 fastboot devices 解锁设备fastboot oem nubia_unlock NUBIA_NX563J 我用的解锁设备是:fastboot flashing unlock 1.打开开发者选项。将OEM解锁的按钮打开 2.下载附件努…...

python 02 List
Python 1-14 列表 第一课 1437. 是否所有 1 都至少相隔 k 个元素 class Solution:def kLengthApart(self, nums: List[int], k: int) -> bool:cnt k # 处理第一个 1for i, x in enumerate(nums):if x 1:if cnt < k: return Falsecnt 0 # 遇到 1 从新记数else: cnt …...
-研发岗)
【秋招笔试】09.28科大讯飞秋招(已改编)-研发岗
🍭 大家好这里是 春秋招笔试突围,一起备战大厂笔试 💻 ACM金牌团队🏅️ | 多次AK大厂笔试 | 大厂实习经历 ✨ 本系列打算持续跟新 春秋招笔试题 👏 感谢大家的订阅➕ 和 喜欢💗 和 手里的小花花🌸 ✨ 笔试合集传送们 -> 🧷春秋招笔试合集 本次的三题全部上线…...

[SAP ABAP] 锁对象
在SAP中使用锁对象,用于避免在数据库中插入或更改数据时出现不一致的情况 1.创建锁对象 数据准备 学校表(ZDBT_SCH_437) 使用事务码SE11创建锁对象 点击"锁对象"单选按钮,输入以E开头的锁定对象的名称,然后点击创建按钮 锁对象名…...

Docker快速部署RabbitMq教程
1、拉取RabbitMQ镜像 docker pull rabbitmq:management RabbitMQ Management 插件为 RabbitMQ 提供了一个基于 Web 的用户界面(Management UI),允许你通过浏览器来监控、管理 RabbitMQ 实例。 因为docker默认是使用的是Docker Hub的官方镜…...

解决银河麒麟V10中/data目录执行权限问题
解决银河麒麟V10中/data目录执行权限问题 1、问题描述2、解决方案步骤一:编辑fstab文件步骤二:重启系统步骤三:验证更改 3、总结 💖The Begin💖点点关注,收藏不迷路💖 在使用银河麒麟桌面操作系…...

画两个数的平方和的曲线
代码1: from mpl_toolkits import mplot3d import numpy as np import matplotlib.pyplot as plt# Creating dataset x np.outer(np.linspace(-3, 3, 32), np.ones(32)) y x.copy().T # transpose z (x **2 y **2 )# Creating figure fig plt.figure(figsize …...

问:进程/线程上下文切换场景及相关概念?
进程、线程以及上下文切换是操作系统和并发编程中不可或缺的概念。这些概念不仅理论意义重大,而且在实际应用中起着至关重要的作用。掌柜将通过具体场景,探讨它们之间的关联以及上下文切换过程。_ 一、进程与线程 进程(有时也称为任务&…...

神经网络(一):神经网络入门
文章目录 一、神经网络1.1神经元结构1.2单层神经网络:单层感知机1.3两层神经网络:多层感知机1.4多层神经网络 二、全连接神经网络2.1基本结构2.2激活函数、前向传播、反向传播、损失函数2.2.1激活函数的意义2.2.2前向传播2.2.3损失函数、反向传播2.2.4梯…...

卸载apt-get 安装的PostgreSQL版本
文章目录 卸载apt-get 安装的PostgreSQL版本查找已安装的PostgreSQL包卸载PostgreSQL:检查并删除残留文件验证卸载 卸载apt-get 安装的PostgreSQL版本 卸载通过apt-get安装的PostgreSQL 就版本,可以按照以下步骤进行。 查找已安装的PostgreSQL包 在卸…...

低代码用户中心:构建高效便捷的用户管理平台
什么是低代码用户中心? 低代码用户中心是一种利用低代码开发平台构建的用户管理系统,允许企业快速创建、部署和管理用户信息、权限及互动记录。通过可视化界面和预置组件,企业可以在短时间内实现灵活的用户管理解决方案,而无需编…...

3款免费的GPT类工具
前言 随着科技的飞速发展,人工智能(AI)的崛起与发展已经成为我们生活中不可或缺的一部分。它的出现彻底改变了我们与世界互动的方式,并为各行各业带来了前所未有的便利。 一、Kimi 网址:点我前往 国产AI模型Kimi是一…...

Mixture-of-Experts (MoE): 条件计算的诞生与崛起【上篇】
大型语言模型(LLM)的现代进步主要是缩放定律的产物[6]。 假设模型是在足够大的数据集上训练出来的,那么随着底层模型规模的增加,我们会看到性能的平滑提升。 这种扩展规律最终促使我们创建了 GPT-3 以及随后的其他(更强…...
)
【算法】分治:归并排序之LCR 170.交易逆序对的总数(hard)
系列专栏 双指针 模拟算法 分治思想 目录 1、题目链接 2、题目介绍 3、解法 4、代码 1、题目链接 LCR 159. 库存管理 III - 力扣(LeetCode) 2、题目介绍 在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一…...

2024.9.28 作业+思维导图
widget.cpp #include "widget.h"Widget::Widget(QWidget *parent): QWidget(parent) {this->setFixedSize(320,448);this->setWindowFlag(Qt::FramelessWindowHint);//QPushButtonQPushButton *PushButton1 new QPushButton("登录",this);PushButto…...
(TODO))
树莓派外挂Camera(基操)(TODO)
(TODO) 手上有OV5647,OV2640,看这次能不能驱动吧。。。 树莓派3B CSI摄像头配置-阿里云开发者社区 你可以使用树莓派3B的CSI接口连接相机模块。首先,确保相机模块正确连接到CSI接口。然后,使用raspi-config…...

讯飞星火编排创建智能体学习(二)决策节点
目录 概述 决策节点 文生图节点 连接节点 测试结果 概述 在上一篇博文讯飞星火编排创建智能体学习(一)最简单的智能体构建-CSDN博客,我介绍了编排创作智能体,这篇来介绍一下“决策节点”。 决策节点 在编排创作智能体中&…...

YOLOv5改进:Unified-loU,用于高品质目标检测的统一loU ,2024年8月最新IoU
💡💡💡现有IoU问题点:IoU (Intersection over Union)作为模型训练的关键,极大地显示了当前预测框与Ground Truth框之间的差异。后续研究者不断在IoU中加入更多的考虑因素,如中心距离、纵横比等。然而,仅仅提炼几何差异是有上限的;而且新的对价指数与借据本身存在潜在…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
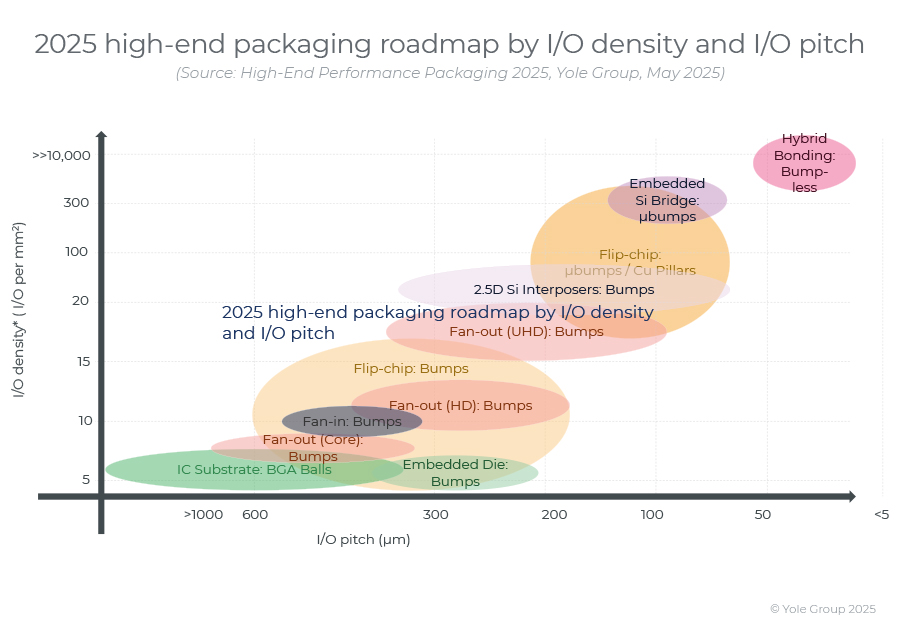
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
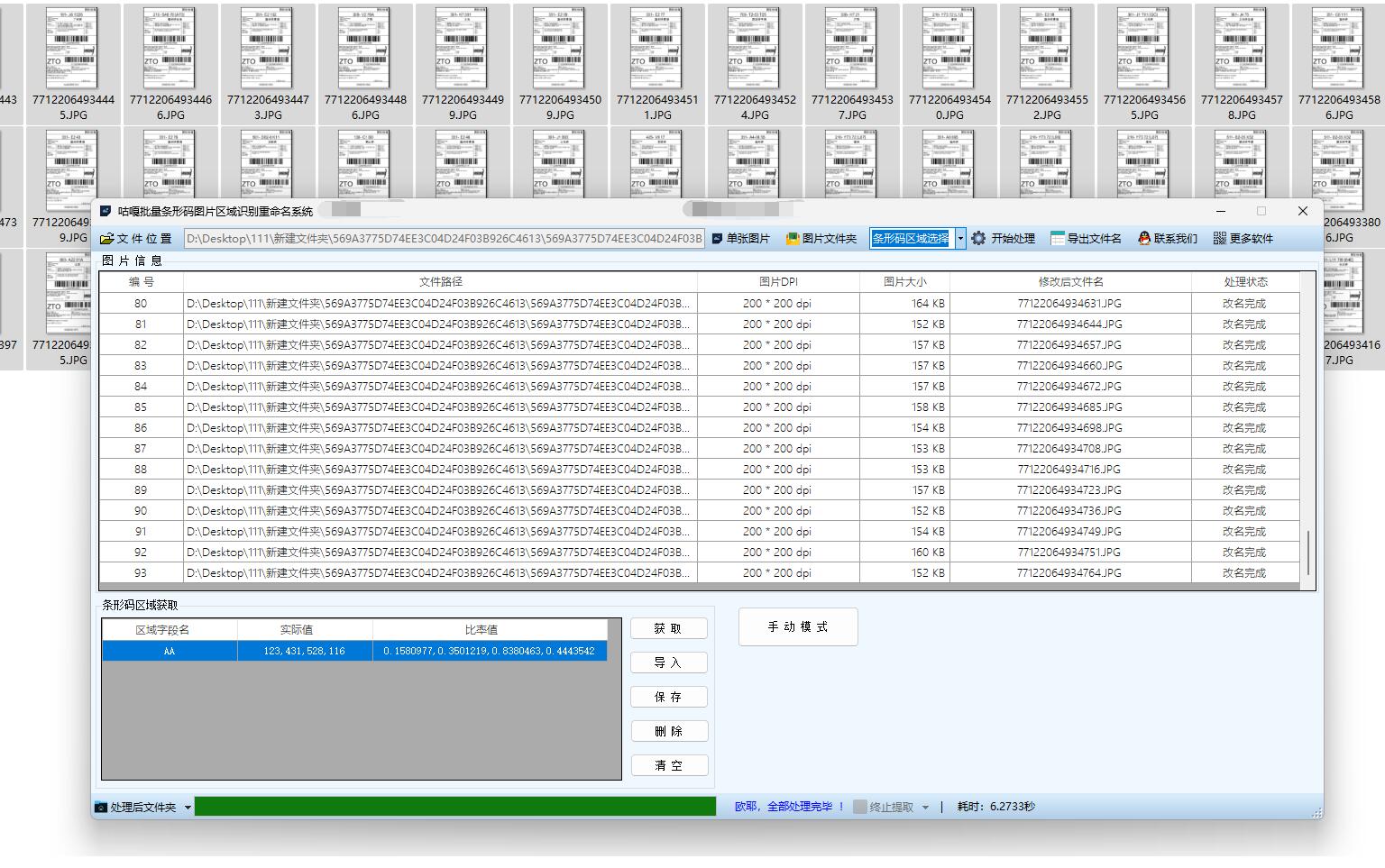
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...
进行稀疏数据预测的技术方案)
结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案
以下是一个结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案,包含完整数学推导、PyTorch/TensorFlow双框架实现代码及对比实验分析。 基于PINN的反应扩散方程稀疏数据预测与大规模数据泛化能力研究 1. 问题定义与数学模型 1.1 反应扩散方程 考虑标…...
