OpenCV入门(二十四)快速学会OpenCV 23 傅里叶变换
OpenCV入门(二十四)快速学会OpenCV 23 傅里叶变换
- 1.傅里叶变换理论概述
- 2.Numpy实现傅里叶变换
- 2.1 傅里叶变换
- 2.2 傅里叶逆变换
- 2.3 高通滤波
- 3.OpenCV实现傅里叶变换
- 3.1 实现傅里叶变换
- 3.2 实现傅里叶逆变换
- 3.3 低通滤波
作者:Xiou
1.傅里叶变换理论概述
图像处理一般分为空间域处理和频率域处理。空间域处理是直接对图像内的像素进行处理。空间域处理主要划分为灰度变换和空间滤波两种形式。灰度变换是对图像内的单个像素进行处理,比如调节对比度和处理阈值等。空间滤波涉及图像质量的改变,例如图像平滑处理。空间域处理的计算简单方便,运算速度更快。
频率域处理是先将图像变换到频率域,然后在频率域对图像进行处理,最后再通过反变换将图像从频率域变换到空间域。傅里叶变换是应用最广泛的一种频域变换,它能够将图像从空间域变换到频率域,而逆傅里叶变换能够将频率域信息变换到空间域内。傅里叶变换在图像处理领域内有着非常重要的作用。
在图像处理过程中,傅里叶变换就是将图像分解为正弦分量和余弦分量两部分,即将图像从空间域转换到频率域(以下简称频域)。数字图像经过傅里叶变换后,得到的频域值是复数。因此,显示傅里叶变换的结果需要使用实数图像(real image)加虚数图像(complex image),或者幅度图像(magnitude image)加相位图像(phase image)的形式。
因为幅度图像包含了原图像中我们所需要的大部分信息,所以在图像处理过程中,通常仅使用幅度图像。当然,如果希望先在频域内对图像进行处理,再通过逆傅里叶变换得到修改后的空域图像,就必须同时保留幅度图像和相位图像。对图像进行傅里叶变换后,我们会得到图像中的低频和高频信息。
低频信息对应图像内变化缓慢的灰度分量。高频信息对应图像内变化越来越快的灰度分量,是由灰度的尖锐过渡造成的。例如,在一幅大草原的图像中有一头狮子,低频信息就对应着广袤的颜色趋于一致的草原等细节信息,而高频信息则对应着狮子的轮廓等各种边缘及噪声信息。
傅里叶变换的目的,就是为了将图像从空域转换到频域,并在频域内实现对图像内特定对象的处理,然后再对经过处理的频域图像进行逆傅里叶变换得到空域图像。傅里叶变换在图像处理领域发挥着非常关键的作用,可以实现图像增强、图像去噪、边缘检测、特征提取、图像压缩和加密等。
高频 vs 低频
高频 vs 低频:
高频: 变换剧烈的灰度分量, 例如边界。
低频: 变换缓慢的灰度分量, 例如一片大海。
滤波:
低通滤波器: 只保留低频, 会使得图像模糊。
高通滤波器: 只保留高频, 会使得图像细节增强。
傅里叶变化 (Fourier Transform) 是一种分析信号的方法. 傅里叶变化可分析信号的成分, 也可以用这些成分合成信号。
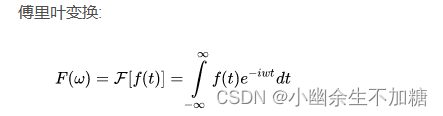
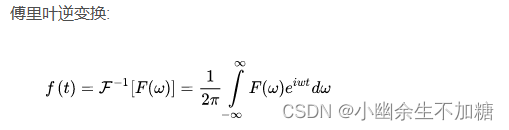
2.Numpy实现傅里叶变换
2.1 傅里叶变换
Numpy模块提供了傅里叶变换功能,Numpy模块中的fft2()函数可以实现图像的傅里叶变换。本节介绍如何用Numpy模块实现图像的傅里叶变换,以及在频域内过滤图像的低频信息,保留高频信息,实现高通滤波。
Numpy提供的实现傅里叶变换的函数是numpy.fft.fft2(),它的语法格式是:
返回值 = numpy.fft.fft2(原始图像)
这里需要注意的是,参数“原始图像”的类型是灰度图像,函数的返回值是一个复数数组(complex ndarray)。
经过该函数的处理,就能得到图像的频谱信息。此时,图像频谱中的零频率分量位于频谱图像(频域图像)[插图]的左上角,为了便于观察,通常会使用numpy.fft.fftshift()函数将零频率成分移动到频域图像的中心位置。如图所示
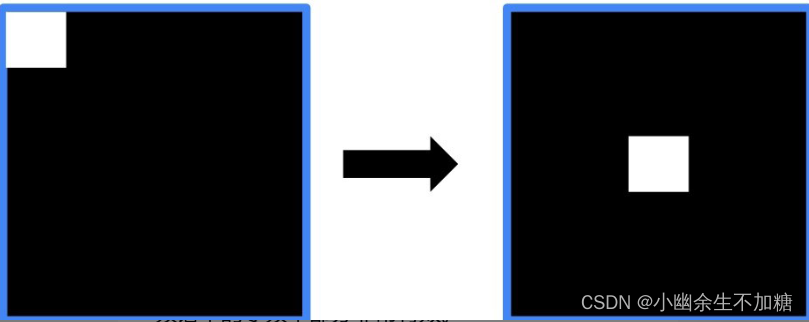
函数numpy.fft.fftshift()的语法格式是:
返回值=numpy.fft.fftshift(原始频谱)
使用该函数处理后,图像频谱中的零频率分量会被移到频域图像的中心位置,对于观察傅里叶变换后频谱中的零频率部分非常有效。对图像进行傅里叶变换后,得到的是一个复数数组。为了显示为图像,需要将它们的值调整到[0,255]的灰度空间内,使用的公式为:
像素新值=20*np.log(np.abs(频谱值))
式中np是“numpy”的缩写,来源于“import numpy as np”,后面不再对此进行说明。
代码实例:用Numpy实现傅里叶变换,观察得到的频谱图像。
import cv2
import numpy as np
import matplotlib.pyplot as pltimg = cv2.imread('girl1.jpg', 0)
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
magnitude_spectrum = 20 * np.log(np.abs(fshift))
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('result')
plt.axis('off')
plt.show()
输出结果:
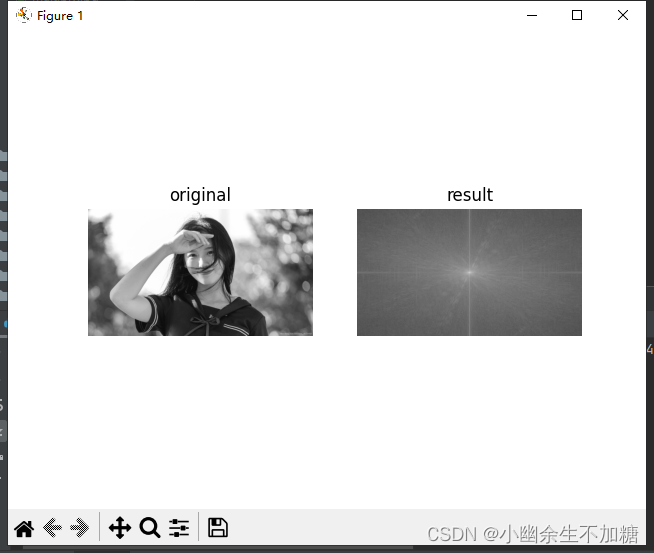
2.2 傅里叶逆变换
需要注意的是,如果在傅里叶变换过程中使用了numpy.fft.fftshift()函数移动零频率分量,那么在逆傅里叶变换过程中,需要先使用numpy.fft.ifftshift()函数将零频率分量移到原来的位置,再进行逆傅里叶变换,该过程如图
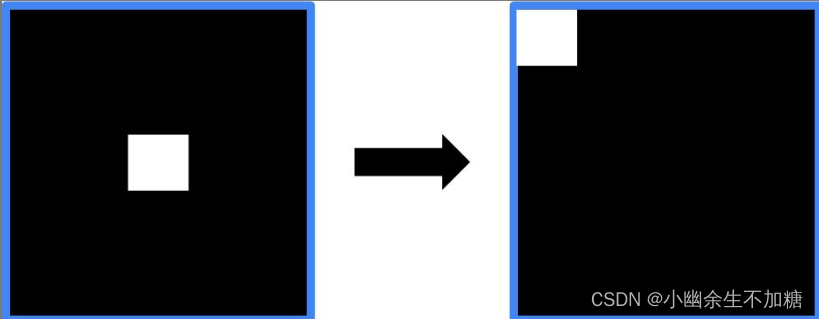
函数numpy.fft.ifftshift()是numpy.fft.fftshift()的逆函数,其语法格式为:
调整后的频谱 = numpy.fft.ifftshift(原始频谱)
numpy.fft.ifft2()函数可以实现逆傅里叶变换,返回空域复数数组。它是numpy.fft.fft2()的逆函数,该函数的语法格式为:
返回值=numpy.fft.ifft2(频域数据)
函数numpy.fft.ifft2()的返回值仍旧是一个复数数组(complex ndarray)。逆傅里叶变换得到的空域信息是一个复数数组,需要将该信息调整至[0, 255]灰度空间内,使用的公式为:
iimg = np.abs(逆傅里叶变换结果)
代码实例:在Numpy内实现傅里叶变换、逆傅里叶变换,观察逆傅里叶变换的结果图像。
import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('girl1.jpg',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f)ishift = np.fft.ifftshift(fshift)iimg = np.fft.ifft2(ishift)#print(iimg)iimg = np.abs(iimg)#print(iimg)plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iimg, cmap = 'gray')plt.title('iimg'), plt.axis('off')plt.show()
输出结果:

2.3 高通滤波
在Numpy内对图像进行傅里叶变换,得到其频域图像。然后,在频域内将低频分量的值处理为0,实现高通滤波。最后,对图像进行逆傅里叶变换,得到恢复的原始图像。观察傅里叶变换前后图像的差异。
代码实例:
import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('image\\boat.bmp',0)f = np.fft.fft2(img)fshift = np.fft.fftshift(f)rows, cols = img.shapecrow, ccol = int(rows/2) , int(cols/2)fshift[crow-30:crow+30, ccol-30:ccol+30] = 0ishift = np.fft.ifftshift(fshift)iimg = np.fft.ifft2(ishift)iimg = np.abs(iimg)plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iimg, cmap = 'gray')plt.title('iimg'), plt.axis('off')plt.show()
输出结果:

3.OpenCV实现傅里叶变换
OpenCV提供了函数cv2.dft()和cv2.idft()来实现傅里叶变换和逆傅里叶变换,下面分别展开介绍。
3.1 实现傅里叶变换
函数cv2.dft()的语法格式为:
返回结果=cv2.dft(原始图像,转换标识)
代码实例:用OpenCV函数对图像进行傅里叶变换,并展示其频谱信息。
import numpy as npimport cv2import matplotlib.pyplot as pltimg = cv2.imread('girl1.jpg',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)result = 20*np.log(cv2.magnitude(dftShift[:, :,0], dftShift[:, :,1]))plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(result, cmap = 'gray')plt.title('result'), plt.axis('off')plt.show()
输出结果:

3.2 实现傅里叶逆变换
在OpenCV中,使用函数cv2.idft()实现逆傅里叶变换,该函数是傅里叶变换函数cv2.dft()的逆函数。其语法格式为:
返回结果=cv2.idft(原始数据)
对图像进行傅里叶变换后,通常会将零频率分量移至频谱图像的中心位置。如果使用函数numpy.fft.fftshift()移动了零频率分量,那么在进行逆傅里叶变换前,要使用函数numpy.fft.ifftshift()将零频率分量恢复到原来位置。
代码实例:用OpenCV函数对图像进行傅里叶变换、逆傅里叶变换,并展示原始图像及经过逆傅里叶变换后得到的图像。
import numpy as npimport cv2import matplotlib.pyplot as pltimg = cv2.imread('girl1.jpg',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)ishift = np.fft.ifftshift(dftShift)iImg = cv2.idft(ishift)iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iImg, cmap = 'gray')plt.title('inverse'), plt.axis('off')plt.show()
输出结果:

3.3 低通滤波
前面讲过,在一幅图像内,低频信号对应图像内变化缓慢的灰度分量。例如,在一幅大草原的图像中,低频信号对应着颜色趋于一致的广袤草原。低通滤波器让高频信号衰减而让低频信号通过,图像进行低通滤波后会变模糊。
代码实例:使用函数cv2.dft()对图像进行傅里叶变换,得到其频谱图像。然后,在频域内将其高频分量的值处理为0,实现低通滤波。最后,对图像进行逆傅里叶变换,得到恢复的原始图像。观察傅里叶变换前后图像的差异。
import numpy as npimport cv2import matplotlib.pyplot as pltimg = cv2.imread('girl1.jpg',0)dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)dftShift = np.fft.fftshift(dft)rows, cols = img.shapecrow, ccol = int(rows/2) , int(cols/2)mask = np.zeros((rows, cols,2), np.uint8)#两个通道,与频域图像匹配mask[crow-30:crow+30, ccol-30:ccol+30] = 1fShift = dftShift*maskishift = np.fft.ifftshift(fShift)iImg = cv2.idft(ishift)iImg= cv2.magnitude(iImg[:, :,0], iImg[:, :,1])plt.subplot(121), plt.imshow(img, cmap = 'gray')plt.title('original'), plt.axis('off')plt.subplot(122), plt.imshow(iImg, cmap = 'gray')plt.title('inverse'), plt.axis('off')plt.show()
输出结果:

运行上述代码,得到如图所示的结果,左图为原始图像,右图为变换后的图像。可以看到,经过低通滤波后,图像的边缘信息被削弱了。
相关文章:

OpenCV入门(二十四)快速学会OpenCV 23 傅里叶变换
OpenCV入门(二十四)快速学会OpenCV 23 傅里叶变换1.傅里叶变换理论概述2.Numpy实现傅里叶变换2.1 傅里叶变换2.2 傅里叶逆变换2.3 高通滤波3.OpenCV实现傅里叶变换3.1 实现傅里叶变换3.2 实现傅里叶逆变换3.3 低通滤波作者:Xiou 1.傅里叶变换…...

线段树合并
前置知识:权值线段树,动态开点。 引入 我们先来看一道题: 永无乡包含 nnn 座岛,给出每座岛的重要度的排名,名次用 111 到 nnn 来表示。一开始有 mmm 条边连接,接下来有 qqq 次操作。操作分两种ÿ…...

研发效能 | DevOps如何改变游戏公司工作方式?
如果你是游戏开发者,那么在过去几年里,你可能会觉得有人给了你一把双刃剑。 整个行业不断蓬勃发展,但玩家的预期值也越来越高。玩家们总是希望游戏体验能够更快、更真实、更具创造性。此外,他们还希望能够定期推出新的游戏和更新…...

Mongo聚合和Springboot整合Mongo聚合
聚合(aggregate)是基于数据处理的聚合管道,每个文档通过一个由多个阶段(stage)组成的管道,可以对每个阶段的管道进行分组、过滤等功能,然后经过一系列的处理,输出相应的结果。 语法格式:db.集合名称.aggregate({管道:{表达式}}) 常用管道如下: $group: 将集合中的⽂…...
第06章_索引的数据结构
第06章_索引的数据结构 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目…...

不确定的市场,确定的增长,海尔智家2022全球再逆增
文|螳螂观察 作者| 余一 上市公司2022年年报逐渐进入密集披露期,在当前的年报季窗口,各家公司的业绩情况被高度关注。 3月30日晚,海尔智家发布了2022年财报。财报显示,2022年海尔智家实现收入2435.14亿元,同比增长7…...

测试老鸟手把手教你python接口自动化测试项目实战演示
目录 前言 一、项目准备 二、项目流程 三、完整代码 四、总结 前言 在进行接口自动化测试项目实战之前,我们需要先了解什么是接口自动化测试。接口自动化测试是通过自动化脚本模拟用户请求和服务器响应的过程,以检测接口是否符合预期,确…...
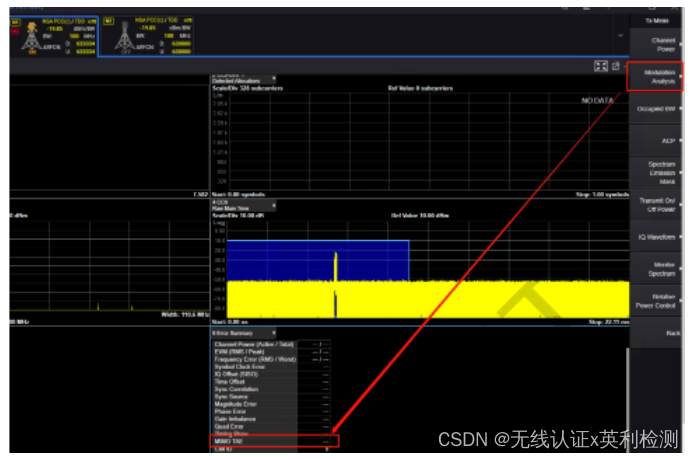
一起来学5G终端射频标准(Coherent UL-MIMO测试要求)
01 — Coherent UL-MIMO测试要求 首先什么是Coherent?它的英文释义是:(of ideas, thoughts, argument, theory, or policy) logical and consistent,翻译过来就是:(看法、思想、论证、理论或政策等&…...

计算广告(五)
Nobid Nobid(在某手有时也叫MCB,在Facebook叫Lowest Cost)是指广告主不用(也不能)对转化成本进行出价,而是出一个预算(大多数是日预算),然后投放平台的目标是在时间范围…...
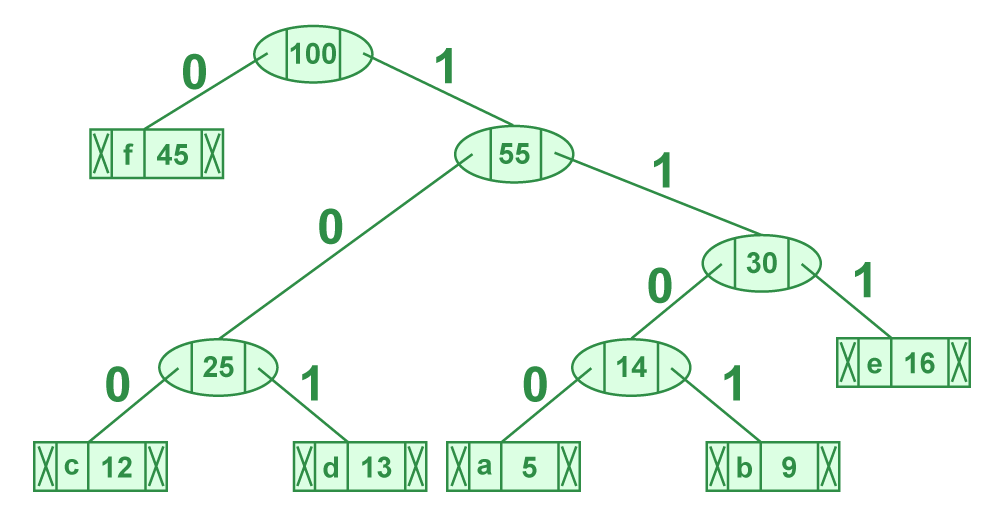
排序输入的高效霍夫曼编码 | 贪心算法 3
前面我们讲到了 贪心算法的哈夫曼编码规则,原理图如下: 如果我们知道给定的数组已排序(按频率的非递减顺序),我们可以在 O(n) 时间内生成霍夫曼代码。以下是用于排序输入的 O(n) 算法。1.创建两个空队列。2.为每个唯一…...

奇异值分解(SVD)和图像压缩
在本文中,我将尝试解释 SVD 背后的数学及其几何意义,还有它在数据科学中的最常见的用法,图像压缩。 奇异值分解是一种常见的线性代数技术,可以将任意形状的矩阵分解成三个部分的乘积:U、S、V。原矩阵A可以表示为&#…...

Java如何从yml文件获取对象
目录一、背景二、application.yml三、ChinaPersonFactory.java四、使用示例一、背景 在 SpringBoot 中,我们可以使用 Value 注解从属性文件(例如 application.yml 或 application.properties)中获取配置信息,但是只能获取简单的字…...
vue使用tinymce实现富文本编辑器
安装两个插件tinymce和 tinymce/tinymce-vue npm install tinymce5.10.3 tinymce/tinymce-vue5.0.0 -S 注意: tinymce/tinymce-vue 是对tinymce进行vue的包装,主要作用当作vue组件使用-S保存到package.json文件 2. 把node_modules/tinymce下的目录&a…...

yolov4实战训练数据
1、克隆项目文件 项目Github地址:https://github.com/AlexeyAB/darknet 打开终端,克隆项目 git clone https://github.com/AlexeyAB/darknet.git无法克隆的话,把https修改为git git clone git://github.com/AlexeyAB/darknet.git修改Makef…...

第十四章 DOM的Diff算法与key
React使用Diff算法来比较虚拟DOM树和真实DOM树之间的差异,并仅更新必要的部分,以提高性能。key的作用是在Diff算法中帮助React确定哪些节点已更改,哪些节点已添加或删除。 我们以案例来说明。 使用索引值和唯一ID作为key的效果 1、使用索引…...

MySQL调优
MySQL调优常见的回答如何回答效果更好业务层的优化如果只能用mysql该如何优化代码层的优化SQL层面优化总结常见的回答 SQL层面的优化——创建索引,创建联合索引,减少回表。再有就是少使用函数查询。 回表指的是数据库根据索引(非主键&#…...
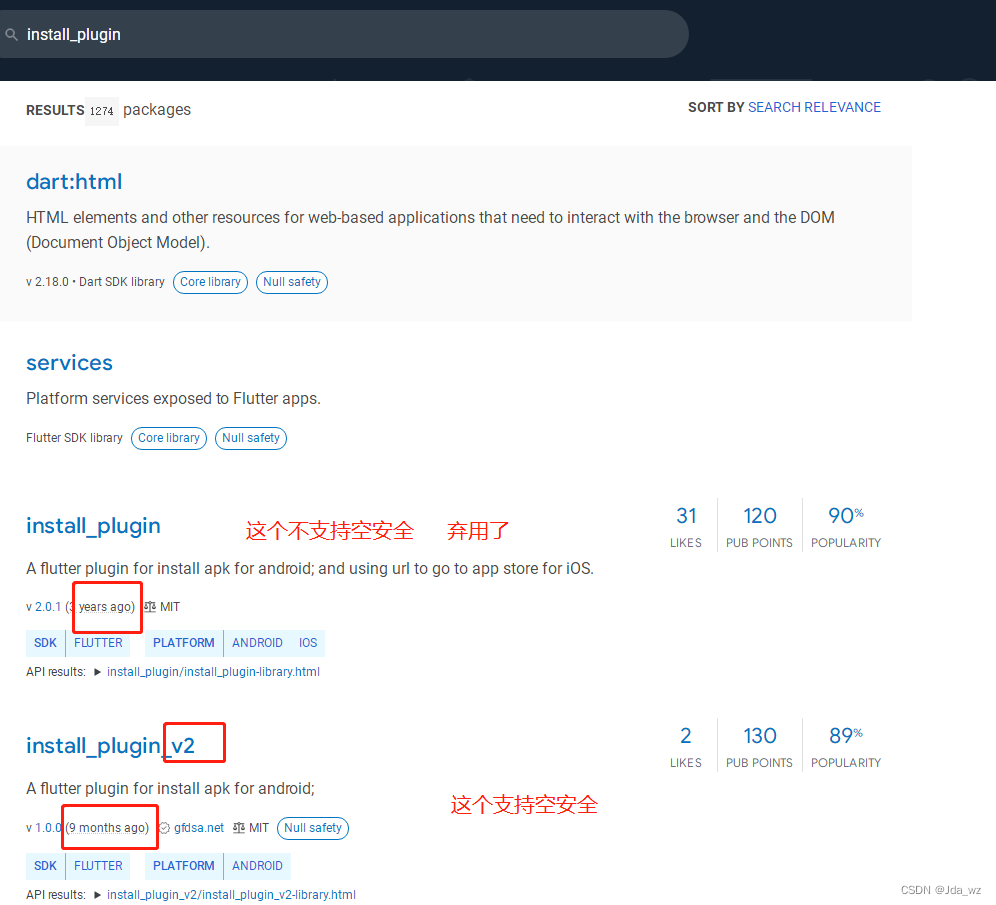
《Flutter进阶》flutter升级空安全遇到的一些问题及解决思路
空安全出来挺久了,由于业务需求较紧,一直没时间去升级空安全,最近花了几天去升级,发现其实升级也挺简单的,不要恐惧,没有想象中的多BUG。 flutter版本从1.22.4升到3.0.5; compileSdkVersion从1…...

最值得入手的五款骨传导耳机,几款高畅销的骨传导耳机
骨传导耳机是一种声音传导方式,主要通过颅骨、骨骼把声波传递到内耳,属于非入耳式的佩戴方式。相比传统入耳式耳机,骨传导耳机不会堵塞耳道,使用时可以开放双耳,不影响与他人的正常交流。骨传导耳机不会对耳朵产生任何…...
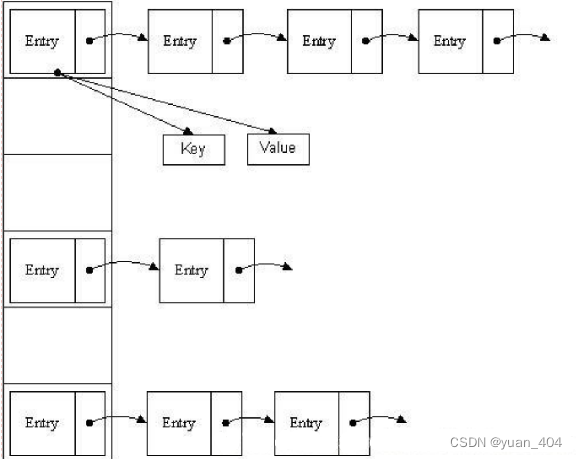
HashMap源码分析 (1.基础入门) 学习笔记
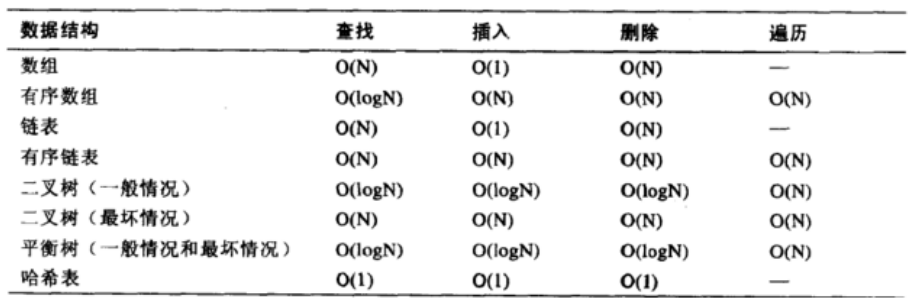
本章为 《HashMap全B站最细致源码分析课程》 拉钩教育HashMap 学习笔记 文章目录1. HashMap的数据结构1. 数组2. 链表3. 哈希表3.1 Hash1. HashMap的数据结构 数据结构中有数组和链表来实现对数据的存储,但这两者基本上是两个极端。 1. 数组 在生成数组的时候数…...

6 使用强制类型转换的注意事项
概述 在C语言中,强制类型转换是通过直接转换为特定类型的方式来实现的,类似于下面的代码。 float fNumber = 66.66f; // C语言的强制类型转换 int nData = (int)fNumber; 这种方式可以在任意两个类型间进行转换,太过随意和武断,很容易带来一些难以发现的隐患和问题。C++为…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
