B树系列解析

- 我最近开了几个专栏,诚信互三!
====> |||《算法专栏》::刷题教程来自网站《代码随想录》。|||
====> |||《C++专栏》::记录我学习C++的经历,看完你一定会有收获。|||
====> |||《Linux专栏》::记录我学习Linux的经历,看完你一定会有收获。|||
====> |||《C#专栏》::记录我复习C#的经历,深度理解,查漏补缺,不定期更新。|||
====> |||《计算机网络专栏》::记录我学习计算机网络,看完你一定会有收获。|||
====> |||《mysql数据库》::记录我学习数据库,看完你一定会有收获。|||
B树系列解析
- B树的优势
- B树的结构
- B树的增加
- B+树的结构
- B+树的插入
- B*树了解
B树的优势
B树系列都擅长外查询,及查询磁盘中的数据,B树都是一棵多叉树,对于二叉搜索树来说,查询到一个结点的时间复杂度位logN,而一颗B树,查询都一个结点的时间复杂的位logM^N,着两者在内存级别时,差别不大,但是在磁盘级别能节约多次磁盘IO的时间,从而大大加快查询的速度。
因此,该数据结构常常用于需要大量进行磁盘IO的情况,如文件系统以及数据库的索引。
B树的结构
B树满足以下几点要求,假设这是一颗M叉树。
1).B树的根结点至少有两个孩子。
2).B树的每个结点要有k个孩子和k-1个关键字,up(M/2)<=k<=M。
3).叶子结点没有孩子只有关键字。
4).B树关键字的左孩子的关键字比当前关键字都小,右孩子关键字比当前关键字大。

B树在设计结构的时候,我们往往会多设计一个关键字结点和孩子结点,这样好判断分裂的情况。
B树的增加
B树插入值时,是插入到叶子结点,此时有两者情况。
1).叶子结点没满,则直接插入。
2).叶子结点满了,则会进行分裂,将结点的关键字的二分之一拷贝到另一个结点,以及其所对应的孩子,同时提取第一个结点的中位数,加入到父节点,让两个结点连接到父节点的中位数下。

更具上述对于B树的插入描述,可知,B树是向右,向上成长的,所以B树天然平衡。
B+树的结构
B+树是B树的新版本,也是mysql中索引使用的数据结构,它相较于B+树存在一些优势。
1).结构更简单,B+树有K个关键字和K个孩子,K[i]号关键字的孩子C[i]比K[i]大,C[i - 1]比K[i]小。
2).B+树的所有插入的值都在叶子结点,叶子结点通过指针相互连接起来。
3).综上,B+树的分支结点存的是索引,而不是值。
4).B+树遍历查询十分方便,所以查询某个范围的值效率高。

B+树也是向右向上生长,所以也天然平衡。
B+树的插入
B+树插入值时,需要先分裂一个结点,插入情况如下。

插入第一个结点,需要先分裂一个,随后每次插入都往叶子结点插入。
如果插入的结点小于叶子结点的最小值,则需要更新父节点的关键字,如果满了,则直接分裂一半关键字和孩子,不需要提取中位数,直接将第二个结点的最小值付给父节点的关键字。
B*树了解
B*树是对B+树的一次优化,以减少B+树的空间浪费。
插入关键字导致结点满了后,将该结点给兄弟结点,如果兄弟结点也满了,则两个结点各自分出1/3给一个新结点。
相关文章:

B树系列解析
我最近开了几个专栏,诚信互三! > |||《算法专栏》::刷题教程来自网站《代码随想录》。||| > |||《C专栏》::记录我学习C的经历,看完你一定会有收获。||| > |||《Linux专栏》࿱…...

docker 部署 WEB IDE
简介 问题描述:GitCode 的 Web IDE 不满足个人使用需求 如何解决:在本机或云服务器部署 Web IDE 如何解决 拉取容器镜像 docker pull coder/code-server 运行 docker run -d --name vscode -p 8080:8080 -p 8443:8443 -e PASSWORD"123456&quo…...

【Android】数据存储
本章介绍Android五种主要存储方式的用法,包括共享参数SharedPreferences、数据库SQLite、SD卡文件、App的全局内存,另外介绍重要组件之一的应用Application的基本概念与常见用法,以及四大组件之一的内容提供器ContentProvider的基本概念与常见…...

个人网络安全的几个重点与防御
1 浏览器 firefox 这是第一选择 如果你真的不明白可以找找各个浏览器漏洞 mail 的危险的 来自与代理和漏洞 浏览器溢出漏洞 实时注意更新就可以 2 防火墙 大家都用windows 只需在 gpedit.msc 设置 但有什么未知漏洞就不得而知了 因为美国的计划问题 网络端口溢出漏洞 但…...

python爬虫 - 初识爬虫
🌈个人主页:https://blog.csdn.net/2401_86688088?typeblog 🔥 系列专栏:https://blog.csdn.net/2401_86688088/category_12797772.html 目录 前言 一、爬虫的关键概念 (一)HTTP请求与响应 ࿰…...

tomcat版本升级导致的umask问题
文章目录 1、问题背景2、问题分析3、深入研究4、umask4.1、umask的工作原理4.2、umask的计算方式4.3、示例4.4、如何设置umask4.5、注意事项 1、问题背景 我们的java服务是打成war包放在tomcat容器里运行的,有一天我像往常一样去查看服务的日志文件,却提…...

Golang | Leetcode Golang题解之第455题分发饼干
题目: 题解: func findContentChildren(g []int, s []int) (ans int) {sort.Ints(g)sort.Ints(s)m, n : len(g), len(s)for i, j : 0, 0; i < m && j < n; i {for j < n && g[i] > s[j] {j}if j < n {ansj}}return }...
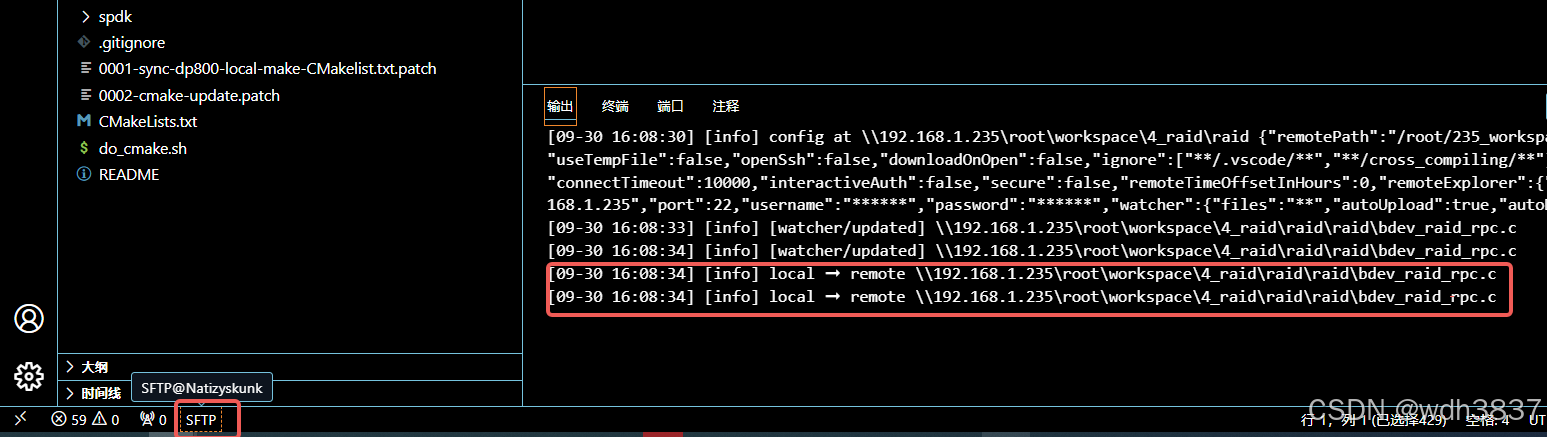
vscode+stfp插件,实现远程自动同步文件代码
概述 远程同步代码,将本地代码实时保存到同一局域网内的另一台电脑(linux系统),这里的本地代码也可以是远程服务上的代码,即从一个远程ip同步到另一台远程ip服务器。 工具 vscode,SFTP插件 安装 vscod…...

python 实现djb2哈希算法
djb2哈希算法介绍 DJB2哈希算法是一种简单且快速的哈希算法,由Daniel J. Bernstein设计。这种算法的实现非常简单,适用于短键值的哈希表,也常被用于嵌入式设备和资源受限的系统。 基本原理 DJB2算法的原理是将输入的字符串视为一个字节数组…...

文件夹作为普通文件而非子模块管理
relaxed_ik_ros2 文件夹下存在 .gitmodules 文件和 .gitignore 文件。这说明该目录已经被 Git 识别为子模块。 要将这个文件夹作为普通文件而非子模块管理,你可以按以下步骤操作: 1. 删除子模块配置 首先删除 .gitmodules 文件中的子模块配置。你可以…...

7c结构体
文章目录 一、结构体的设计二、结构体变量的初始化2.1结构体在内存表示;**2.2**结构体类型声明和 结构体变量的定义和初始化只声明结构体类型声明类型的同时定义变量p1用已有结构体类型定义结构体变量p2*定义变量的同时赋初值。*匿名声明结构体类型 2.3 结构体嵌套及…...

浅聊前后端分离开发和前后端不分离开发模式
1.先聊聊Web开发的开发框架Spring MVC 首先要知道,Spring MVC是Web开发领域的一个知名框架,可以开发基于请求-响应模式的Web应用。而Web开发的本质是遵循HTTP(Hyper Text Transfer Protocol: 超文本传输协议)协议【发请求…...
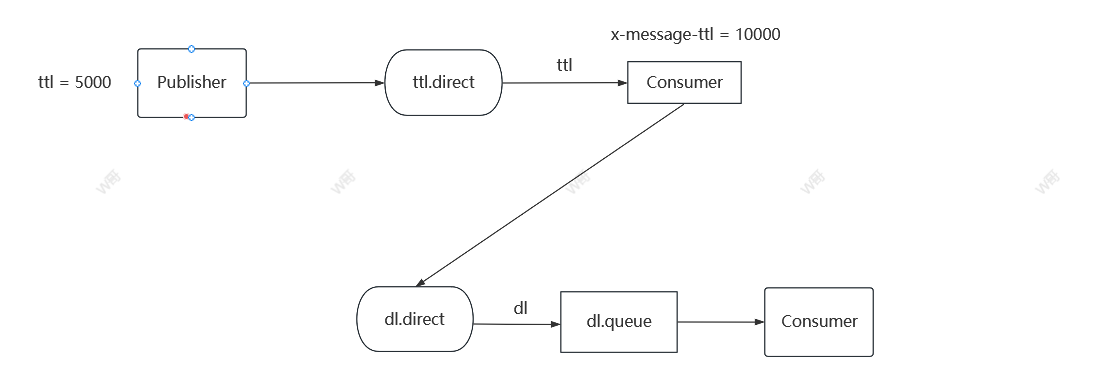
RabbitMQ篇(死信交换机)
目录 一、简介 二、TTL过期时间 三、应用场景 一、简介 当一个队列中的消息满足下列情况之一时,可以成为死信(dead letter) 消费者使用basic.reject或者basic.nack声明消费失败,并且消息的requeue参数设置为false消息是一个过…...

HBase 的 MemStore 详解
一、MemStore 概述 MemStore 是 HBase 的内存存储区域,它是一个负责缓存数据写入操作的组件。每当有写操作(如 Put 或 Delete)发生时,数据会首先被写入到 MemStore 中,而不是直接写入磁盘。MemStore 类似于数据库中的缓…...

【嵌入式软件-数据结构与算法】01-数据结构
摘录于老师的教学课程~~(*๓╰╯๓)~~内含链表、队列、栈、循环队列等详细介绍~~ 基础知识系列 有空再继续更~~~ 目录 【链表】 一、单链表 1、存储结构:带头结点的单链表 2、单链表结点类型的定义 3、创建单链表 1)头插法 2)尾插法 …...

Windows应用开发-解析AVI视频文件
本Windows应用解析AVI视频文件,以表格的方式显示AVI文件结构。并可以将结果保存到bmp图片。下面是,使用该应用解析一部AVI电影获得的图片。 应用开发信息 定义一个INFO结构,包含两个字符串对象,一个ULONGLONG变量,和…...

探索TCP协议的奥秘:Python中的网络通信
引言 在网络通信的世界里,TCP协议(传输控制协议)就如同一座桥梁,连接着数据的发送方和接收方。作为一名拥有20年实战经验的编码专家,我深知TCP协议在构建稳定、可靠的网络应用中的重要性。今天,我将带领大…...

每日学习一个数据结构-树
文章目录 树的相关概念一、树的定义二、树的基本术语三、树的分类四、特殊类型的树五、树的遍历六、树的应用场景 树的遍历一、前序遍历二、中序遍历三、后序遍历使用java代码实现遍历总结 树的相关概念 树是一种重要的非线性数据结构,在计算机科学中有着广泛的应用…...
)
简单PCL库读文件(linux vscode编译)
#include <pcl/io/pcd_io.h> #include <pcl/point_types.h> #include <pcl/common/common.h> #include <iostream>int main(int argc, char** argv) {if (argc ! 2) {std::cerr << "请指定 PCD 文件路径" << std::endl;return -…...

【自动驾驶】最近计划看的论文
将对应的论文链接贴出来,当作监督自己。 方向:端到端自动驾驶 方法论文代码UniADhttps://arxiv.org/pdf/2212.10156https://github.com/OpenDriveLab/UniADVADhttps://arxiv.org/pdf/2303.12077https://github.com/hustvl/VADUADhttps://arxiv.org/pdf…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...

解决MybatisPlus使用Druid1.2.11连接池查询PG数据库报Merge sql error的一种办法
目录 前言 一、问题重现 1、环境说明 2、重现步骤 3、错误信息 二、关于LATERAL 1、Lateral作用场景 2、在四至场景中使用 三、问题解决之道 1、源码追踪 2、关闭sql合并 3、改写处理SQL 四、总结 前言 在博客:【写在创作纪念日】基于SpringBoot和PostG…...

【自然语言处理】大模型时代的数据标注(主动学习)
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构D 实验设计E 个人总结 A 论文出处 论文题目:FreeAL: Towards Human-Free Active Learning in the Era of Large Language Models发表情况:2023-EMNLP作者单位:浙江大…...

C++信息学竞赛中常用函数的一般用法
在C 信息学竞赛中,有许多常用函数能大幅提升编程效率。下面为你介绍一些常见函数及其一般用法: 一、比较函数 1、max()//求出a,b的较大值 int a10,b5,c;cmax(a,b);//得出的结果就是c等于10. 2、min()//求出a,b的较小值 int a1…...
