【堆排】为何使用向下调整法建堆比向上调整法建堆更好呢?
文章目录
- 前言
- 一、堆排代码
- 一、计算使用==向上调整法==建堆的时间复杂度
- 二、计算使用==向下调整法==插入的时间复杂度
- 总结
前言
在博主的上一篇博客堆排(链接在这里点击即可)的总结中提出啦使用向下调整法建堆比使用向上调整法建堆更好,是因为使用向上调整法建堆的时间复杂度为O(n*logn),使用向下调整法建堆的时间复杂度为O(n)。接下来博主就教大家如何计算它们的时间复杂度。
一、堆排代码
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
//向上调整法
void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0)//不需要等于,child只要走到根节点的位置,根节点没有父节点不需要交换{if (arr[child] < arr[parent])//若孩子结点比父结点小则交换{Swap(&arr[parent], &arr[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){//找左右孩子中找最小的if (child + 1 < n && arr[child] > arr[child + 1]){child++;}if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
//堆排
void HeapSort(int* arr, int n)
{//向上调整法建堆for (int i = 0; i < n; i++){AdjustUp(arr, i);}//向下调整算法建堆//for (int i = (n-1-1)/2; i >= 0; i--)//{// AdjustDown(arr, i , n);//}//循环将堆顶数据跟最后位置的数据进行交换int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}一、计算使用向上调整法建堆的时间复杂度
for (int i = 0; i < n; i++)
{AdjustUp(arr, i);
}
- 第1层,20个结点,最多需要向上移动0次。
- 第2层,21个结点,最多需要向下移动1次。
- 第3层,22个结点,最多需要向上移动2次。
- …
- 第h-1层,2h-2个结点,最多需要向上移动h-2次。
- 第h层,2h-1个结点,最多需要向上移动h-1次。
所以最多移动的次数总和为:
(1) T(h) = 20(0)+21(1)+22(2)+…+2h-2(h-2)+2h-1(h-1)
(2) 2T(h) = 21(0)+22(1)+23(2)+…+2h-1(h-2)+2h(h-1)
(2)-(1) 得
T(h) = -(21+22+23+…+2h-2+2h-1+2h-1)+2hh
使用高中阶段学过的等比数列求和公式:S = a1(1-qn)/1-q可得
T(h) = 2(1-2h)+2hh = 2+2h(h-2)
再根据二叉树的性质:n = 2h-1,h = log2(n+1)可得
T(n) = 2 + (n+1)(log2(n+1)-2) = (n+1)log2(n+1)-2n
所以向上调整法建堆的时间复杂度为O(logn*n)
二、计算使用向下调整法插入的时间复杂度
for (int i = (n-1-1)/2; i >= 0; i--)
{AdjustDown(arr, i , n);
}
- 第1层,20个结点,最多需要向下移动h-1次。
- 第2层,21个结点,最多需要向下移动h-2次。
- 第3层,22个结点,最多需要向下移动h-3次。
- …
- 第h-1层,2h-2个结点,最多需要向下移动1次。
- 第h层,2h-1个结点,最多需要向下移动0次。
所以最多移动的次数总和为:
(1) T(h) = 20(h-1)+21(h-2)+22(h-3)+…+2h-2(1)
(2) 2T(h) = 21(h-1)+22(h-2)+23(h-3)+…+2h-1(1)
(2)-(1) 得
T(h) = 21+22+23+…+2h-2+2h-1-20(h-1)
T(h) =20+ 21+22+23+…+2h-2+2h-1-h
使用高中阶段学过的等比数列求和公式:S = a1(1-qn)/1-q可得
T(h) = 2h-1-h
再根据满二叉树的性质:n = 2h-1,h = log2(n+1)可得
T(n) = n-log2(n+1)*
所以向下调整法建堆的时间复杂度为O(n)
总结
通过这篇博客相信柚柚们已经清楚向下调整法建堆和向上调整法建堆的时间复杂度怎么计算啦,后期博主还会更新有关数据结构的博客,感兴趣的柚柚们可以关注博主喔~
相关文章:

【堆排】为何使用向下调整法建堆比向上调整法建堆更好呢?
文章目录 前言一、堆排代码一、计算使用向上调整法建堆的时间复杂度二、计算使用向下调整法插入的时间复杂度总结 前言 在博主的上一篇博客堆排(链接在这里点击即可)的总结中提出啦使用向下调整法建堆比使用向上调整法建堆更好,是因为使用向上调整法建堆的时间复杂…...

在Stable Diffusion WebUI中安装SadTalker插件时几种错误提示的处理方法
SD中的插件一般安装比较简单,但也有一些插件安装会比较难。比如我在安装SadTalker时,就遇到很多问题,一度放弃了,后来查了一些网上攻略,自己也反复查看日志,终于解决,不吐不快。 一、在Stable …...

使用ffmpeg合并视频和音频
使用ffmpeg合并视频和音频 - 哔哩哔哩 简介 FFmpeg是一套可以用来记录、转换数字音频、视频,并能将其转化为流的开源计算机程序。采用LGPL或GPL许可证。它提供了录制、转换以及流化音视频的完整解决方案。它包含了非常先进的音频/视频编解码库libavcodec࿰…...
)
周末总结(2024/10/05)
工作 人际关系核心实践: 要学会随时回应别人的善意,执行时间控制在5分钟以内 坚持每天早会打招呼 遇到接不住的话题时拉低自己,抬高别人(无阴阳气息) 朋友圈点赞控制在5min以内,职场社交不要放在5min以外 职场的人际关系在面对利…...

在Ubuntu中自动挂载SMB/CIFS共享
文章目录 0. 引言1. 使用credentials文件存储认证信息2. 挂载点的准备3. 必要软件的安装4. 调整挂载参数5. 测试挂载6. 日志调试 0. 引言 本文是自己挂载共享磁盘的实践记录,将详细介绍如何在Linux系统中配置自动挂载SMB/CIFS共享,并提供一些常见问题的…...

pWnOS2.0 靶机渗透( cms 渗透,php+mysql 网站渗透,密码碰撞)
pWnOS2.0 靶机渗透( ) 靶机介绍 vulnhub 靶机 本地搭建 由于靶机特性,靶机网卡位nat模式扫不到,原来需要改 nat 的地址 参考方法 https://blog.csdn.net/Bossfrank/article/details/131415257 作者主页 https://blog.csdn.net/Bossfrank?typeblog P…...

【AI】AIOT简介
随着技术的快速发展,人工智能AI和物联网IoT已经成为当今最热门的技术领域。AIOT是人工智能和物联网的结合,使物联网设备更加智能化,能够进行自主决策和学习的技术。 通过物联网产生、收集来自不同维度的、海量的数据存储于云端、边缘端&#…...

picgo + typora + gitee图床
Picgo打造个人图床,稳定又安全 解决Typora笔记上传到CSDN图片无法显示的问题 typora中...

【路径规划】多机器人路径规划
摘要 多机器人路径规划在现代自动化、仓储管理及智能交通系统中有着广泛的应用。本文提出了一种基于A*算法的多机器人路径规划方法,旨在解决多机器人在同一环境中的路径冲突问题。通过采用启发式搜索和路径优化策略,机器人能够在保持避障的前提下实现最…...

深度学习Day-35:One-hot独热编码
🍨 本文为:[🔗365天深度学习训练营] 中的学习记录博客 🍖 原作者:[K同学啊 | 接辅导、项目定制] 一、 独热编码原理 独热编码(One-Hot Encoding)是一种将分类数据转换为二进制向量的方法&#…...

Streamlit 实现登录注册验证
在开发基于 Streamlit 的应用时,用户认证功能是一个常见需求。本文将介绍如何通过两种方式来实现登录注册功能:手动实现 和 使用 Streamlit-Authenticator 库。手动实现虽然灵活,但需要自行处理密码加密、验证等细节;而 Streamlit…...

ASP.NET Zero 多租户介绍
ASP.NET Zero 是一个基于 ASP.NET Core 的应用程序框架,它提供了多租户支持,以下是关于 ASP.NET Zero 多租户的介绍: 一、多租户概念 多租户是一种软件架构模式,允许多个客户(租户)共享同一套软件应用程序…...

【60天备战2024年11月软考高级系统架构设计师——第29天:微服务架构——微服务的优缺点】
微服务架构通过将大型单体应用拆分为多个独立的小型服务,使系统具备灵活性、可扩展性和独立部署的优势。但与此相伴的是复杂的运维和开发管理挑战。因此,在选择微服务架构时,架构师需仔细权衡其优势与劣势。 微服务架构的优点 独立部署&…...

读论文、学习时 零碎知识点记录01
1.入侵检测技术 2.深度学习、机器学习相关的概念 ❶注意力机制 ❷池化 ❸全连接层 ❹Dropout层 ❺全局平均池化 3.神经网络中常见的层...

图解C#高级教程(一):委托
什么是委托 可以认为委托是持有一个或多个方法的对象。但它与对象不同,因为委托可以被执行。当执行委托时,委托会执行它所“持有”的方法。先看一个完整的使用示例。 // See https://aka.ms/new-console-template for more informationdelegate void M…...

CMSIS-RTOS V2封装层专题视频,一期视频将常用配置和用法梳理清楚,适用于RTX5和FreeRTOS(2024-09-28)
【前言】 本期视频就一个任务,通过ARM官方的CMSIS RTOS文档,将常用配置和用法给大家梳理清楚。 对于初次使用CMSIS-RTOS的用户来说,通过梳理官方文档,可以系统的了解各种用法,方便大家再进一步的自学或者应用&#x…...

渗透测试入门学习——使用python脚本自动识别图片验证码,OCR技术初体验
写在前面 由于验证码在服务端生成后存储在服务器的session中,而标用于标识用户身份的sessionid存在于用户cookie中 所以本次识别验证码时需要用requests.session()创建会话对象,模拟真实的浏览器行为,保持与服务器的会话才能获取登录时服务…...

docker环境下配置cerbot获取免费ssl证书并自动续期
文章目录 实践场景了解certbot查看nginx的映射情况操作目标配置nginx配置的ssl证书设置自动续签 实践场景 本人使用docker部署了一个nginx容器,通过容器卷,实现本地html,ssl,conf和ngiinx容器映射的, 经常需要手动部署…...

Studying-多线程学习Part1-线程库的基本使用、线程函数中的数据未定义错误、互斥量解决多线程数据共享问题
来源:多线程编程 线程库的基本使用 两个概念: 进程是运行中的程序线程是进程中的进程 串行运行:一次只能取得一个任务并执行这一个任务 并行运行:可以同时通过多进程/多线程的方式取得多个任务,并以多进程或多线程…...
Flink 03 | 数据流基本操作
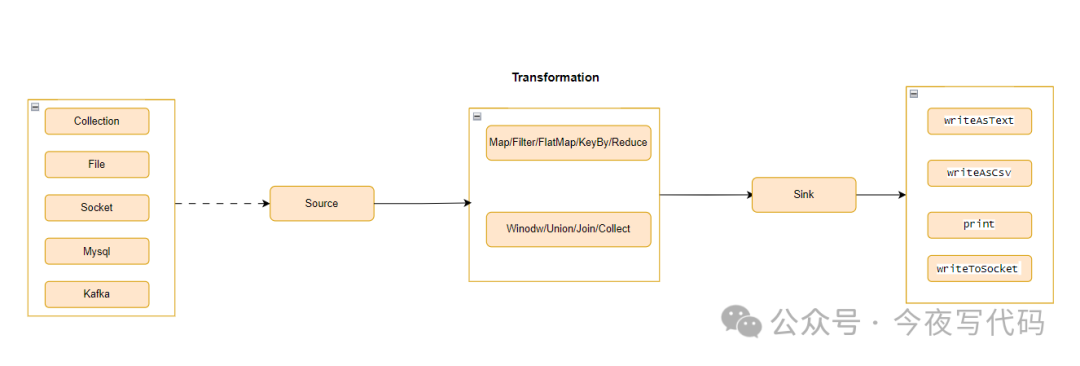
Flink数据流结构 DataStream 转换 通常我们需要分析的业务数据可能存在如下问题: 数据中包含一些我们不需要的数据 数据格式不方面分析 因此我们需要对原始数据流进行加工,比如过滤、转换等操作才可以进行数据分析。 “ Flink DataStream 转换主要作…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

RLHF vs RLVR:对齐学习中的两种强化方式详解
在语言模型对齐(alignment)中,强化学习(RL)是一种重要的策略。而其中两种典型形式——RLHF(Reinforcement Learning with Human Feedback) 与 RLVR(Reinforcement Learning with Ver…...
