C#,码海拾贝(11)——拉格朗日(Lagrange)三点式曲面插值算法,《C#数值计算算法编程》源代码升级改进版
本文开始是曲面插值(Surface Interpolation,也称作:二维插值,二元插值)。
数值计算三点式
数值计算三点式是一种常见的数值计算方法,它是通过对已知函数在某个点及其左右两个点处的函数值进行数值插值,得到该函数在该点处的近似值。数值计算三点式是数值计算中最基本的插值方法之一,也是其它高级插值方法的基础。
数值计算三点式的基本思想是,通过连接已知点,构造一个二次函数,来近似估计未知点处的函数值。如果已知函数在某个点x0处的函数值f(x0),以及其左右两个点x1和x2处的函数值f(x1)和f(x2),则可以构造一个二次函数,通过这个二次函数来估计函数在任意一个x处的函数值。具体来说,可以采用拉格朗日插值法或牛顿插值法求解。
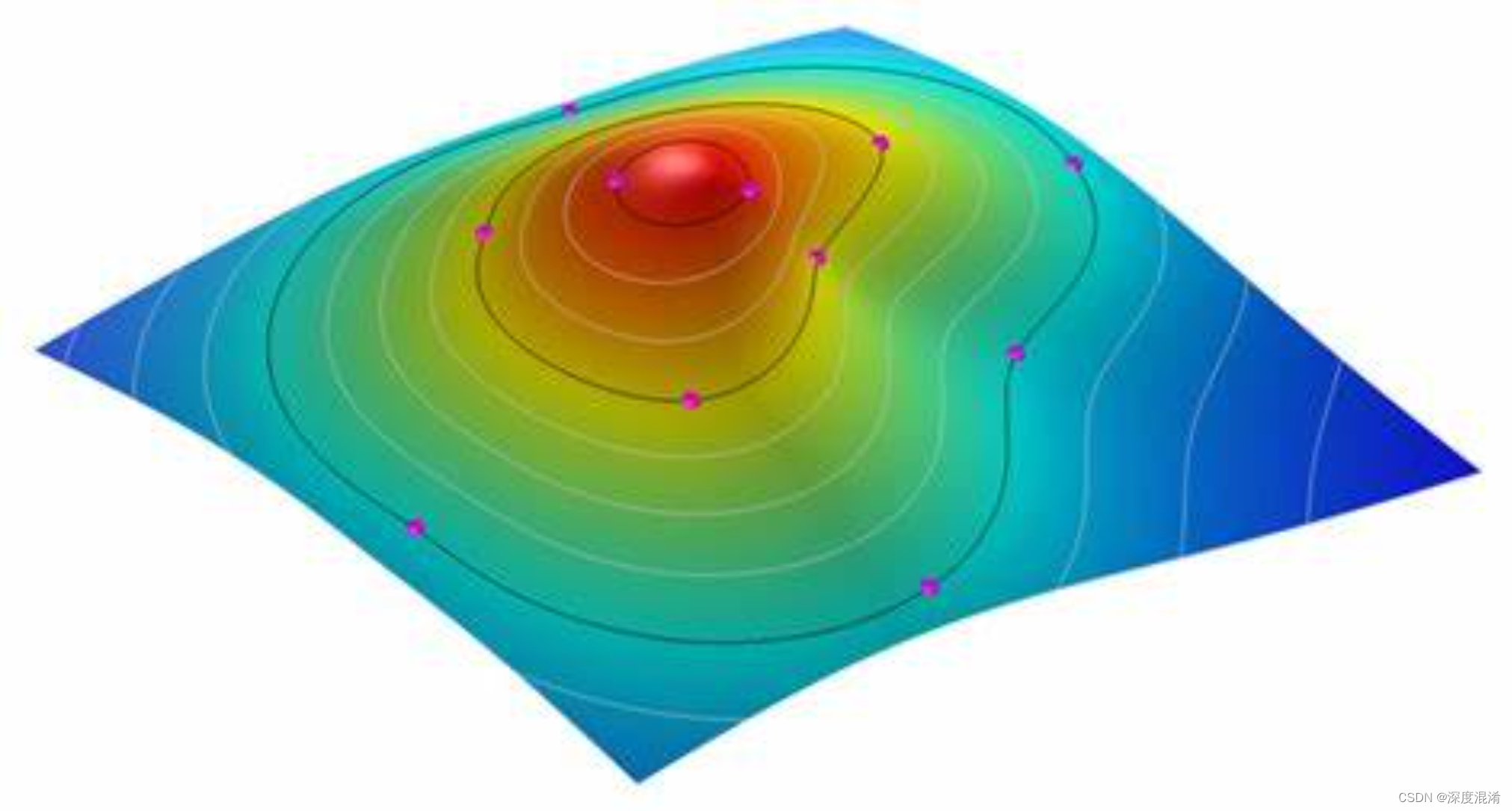
拉格朗日插值(Lagrange interpolation)是一种多项式插值方法,指插值条件中不出现被插函数导数值,过n+1个样点,满足如下图的插值条件的多项式。也叫做拉格朗日公式。
对于一维曲线的插值,一般用到的函数yi=interp1(X,Y,xi,method) ,其中method包括nearst,linear,spline,cubic。
对于二维曲面的插值,一般用到的函数zi=interp2(X,Y,Z,xi,yi,method),其中method也和上面一样,常用的是cubic。
多维曲面法是用来描绘不规则曲面的一种插值技术,经常用于地形学的插值计算中.此方法利用以二次函数为基函数所建立的曲面来描述整个对象,其中最常用的是圆形双叶双曲线.由于描述该方法的控制方程恒有解,因此又称该方法是双调和的.
拟合与插值的区别:
1、在含义上不同:插值是指函数在多个离散点上的函数值或导数信息。通过求解函数中待定形式和待定系数的插值函数,该函数满足给定离散点的约束。
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
拟合是指将平面上的一系列点与光滑曲线连接起来。因为这个曲线有无数的可能性,所以有多种拟合方法。拟合曲线一般可以用函数来表示。根据不同的功能,有不同的拟合名称。
常用的拟合方法有如最小二乘曲线拟合法等,在MATLAB中也可以用polyfit 来拟合多项式。
2、在图像上是不同:图像中的插值必须通过数据,图像中的拟合必须得到最接近的结果,这取决于整体效果。MATLAB做曲线拟合可以通过内建函数或者曲线拟合工具箱(Curve Fitting Toolbox)。这个工具箱集成了用MATLAB建立的图形用户界面(GUIs)和M文件函数。
利用这个工具箱可以进行参数拟合(当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟合),或者通过采用平滑样条或者其他各种插值方法进行非参数拟合(当回归系数不具有物理意义并且不在意他们的时候,就采用非参数拟合方法)。
利用这个界面,可以快速地在简单易用的环境中实现许多基本的曲线拟合。
拟合与插值的区别:
1、在含义上不同:插值是指已知某函数的在若干离散点上的函数值或者导数信息,通过求解该函数中待定形式的插值函数以及待定系数,使得该函数在给定离散点上满足约束。
而拟合是指,拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。拟合的曲线一般可以用函数表示,根据这个函数的不同有不同的拟合名字。
2、在图像上是不同:插值在图像是一定得过了数据的才行;拟合在图像上是必须要得到最接近得结果,是要看总体的效果。
3、在几何意义上不同:拟合是给定了空间中的一些点,找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的)连续曲面来穿过这些点。
using System;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;namespace Zhou.CSharp.Algorithm
{/// <summary>/// 插值计算类Interpolation.cs/// 作者:周长发/// 改编:深度混淆/// https://blog.csdn.net/beijinghorn/// </summary>public static partial class Interpolation{/// <summary>/// 二维三点插值/// </summary>/// <param name="x">一维数组,长度为n,存放给定n x m 个结点x方向上的n个值x(i)</param>/// <param name="y">一维数组,长度为m,存放给定n x m 个结点y方向上的m个值y(i)</param>/// <param name="z">一维数组,长度为n x m,存放给定的n x m个结点的函数值z(i,j),z(i,j) = f(x(i), y(j)), i=0,1,...,n-1, j=0,1,...,m-1</param>/// <param name="u">存放插值点x坐标</param>/// <param name="v">存放插值点y坐标</param>/// <returns>指定函数值f(u, v)</returns>public static double Lagrange_3Points_2D(double[] x, double[] y, double[] z, double u, double v){// x方向上给定结点的点数int n = x.Length;// y方向上给定结点的点数int m = y.Length;// 初值int nn = 3;// 特例int ip;if (n <= 3){ip = 0;nn = n;}else if (u <= x[1]){ip = 0;}else if (u >= x[n - 2]){ip = n - 3;}else{int i = 1;int j = n;while (((i - j) != 1) && ((i - j) != -1)){int w = (i + j) / 2;if (u < x[w - 1]){j = w;}else{i = w;}}if (Math.Abs(u - x[i - 1]) < Math.Abs(u - x[j - 1])){ip = i - 2;}else{ip = i - 1;}}int mm = 3;int iq;if (m <= 3){iq = 0;mm = m;}else if (v <= y[1]){iq = 0;}else if (v >= y[m - 2]){iq = m - 3;}else{int i = 1;int j = m;while (((i - j) != 1) && ((i - j) != -1)){int w = (i + j) / 2;if (v < y[w - 1]){j = w;}else{i = w;}}if (Math.Abs(v - y[i - 1]) < Math.Abs(v - y[j - 1])){iq = i - 2;}else{iq = i - 1;}}double[] b = new double[3];for (int i = 0; i <= nn - 1; i++){b[i] = 0.0;for (int j = 0; j <= mm - 1; j++){int k = m * (ip + i) + (iq + j);double h = z[k];for (k = 0; k <= mm - 1; k++){if (k != j){h = h * (v - y[iq + k]) / (y[iq + j] - y[iq + k]);}}b[i] = b[i] + h;}}double zv = 0.0;for (int i = 0; i <= nn - 1; i++){double h = b[i];for (int j = 0; j <= nn - 1; j++){if (j != i){h = h * (u - x[ip + j]) / (x[ip + i] - x[ip + j]);}}zv = zv + h;}return (zv);}}
}
POWER BY 315SOFT.COM
基于坐标点的计算,从点集计算插值曲线等拓展方法请参阅《拉格朗日插值算法及其拓展》
相关文章:

C#,码海拾贝(11)——拉格朗日(Lagrange)三点式曲面插值算法,《C#数值计算算法编程》源代码升级改进版
本文开始是曲面插值(Surface Interpolation,也称作:二维插值,二元插值)。 数值计算三点式 数值计算三点式是一种常见的数值计算方法,它是通过对已知函数在某个点及其左右两个点处的函数值进行数值插值&…...
CentOS7系统安装MySQL 5.7
目录一、官网下载mysql5.7二、检查mysql依赖环境三、安装MySQL 5.7.281.将安装程序拷贝到/opt目录下2.安装四个安装包3.查看mysql版本4.服务的初始化5.启动mysql,并查看状态(加不加.service后缀都可以)6.查看mysql服务是否自启动(默认自启动)…...

基于粒子群算法优化BP神经网络的高炉si预测,PSO-BP
目录 摘要 BP神经网络的原理 BP神经网络的定义 BP神经网络的基本结构 BP神经网络的神经元 BP神经网络的激活函数, BP神经网络的传递函数 粒子群算法的原理及步骤 基于粒子群算法改进优化BP神经网络的用电量预测 代码 效果图 结果分析 展望 参考 摘要 一般用启发式算法改进B…...

STM32输出PWM波控制电机转速,红外循迹避障智能车+L298N的详细使用手册、接线方法及工作原理,有代码
智能循迹红外避障小车 本设计的完整的系统主要包括STM32单片机最小系统、L298n电机驱动,超声波 ,舵机 ,红外模块等。寻迹小车相信大家都已经耳熟能祥了。 我们在这里主要讲一下L298N驱动电机和单片机输出PWM控制电机转速。 本设计软件系统采…...

3、AI的道德性测试
AI的道德性 AI系统的道德性如何保障是一个重要而复杂的问题,涉及到人工智能的发展、应用、监管、伦理、法律等多个方面。保障AI系统的道德性是一个很重要的问题,因为AI系统不仅会影响人类的生活和工作,也会涉及人类的价值观和伦理道德原则。针对这部分,也需要测试AI系统是…...

银行数字化转型导师坚鹏:银行业务需求分析师技能快速提升之道
银行业务需求分析师技能快速提升之道 ——以推动银行战略目标实现为核心,实现知行果合一课程背景: 很多银行都在开展业务需求分析工作,目前存在以下问题急需解决:不知道银行业务需求分析师掌握哪些关键知识?不清楚…...

C++IO流
文章目录一、CIO流体系二、C标准IO流三、C文件IO流1.ifstream2.ofstream一、CIO流体系 C流是指信息从外部输入设备向计算机内部输入,从内存向外部输出设备输出的过程,这种输入输出的过程非常形象地被称为流的概念。IO流指的就是输入输出流。 我们平时对…...
交友项目【后端环境搭建】
目录 1:环境搭建 1.1:MYSQL数据库 1.1.1:导入相应的sql 1.2:Linux中的docker-compose方法集中部署 1.2.1:介绍 1.3:IDEA设置 1.3.1:基本要求 1.3.2:设置项目编码格式 1.3.3&…...

大事务问题解决方案
文章目录 大事务引发的问题解决办法少用@Transactional注解将查询(select)方法放到事务外事务中避免远程调用事务中避免一次性处理太多数据非事务执行异步处理总结大事务引发的问题 1、死锁 2、回滚时间长 3、并发情况下数据库连接池被占满 4、锁等待 5、接口超时 6、数据库主…...
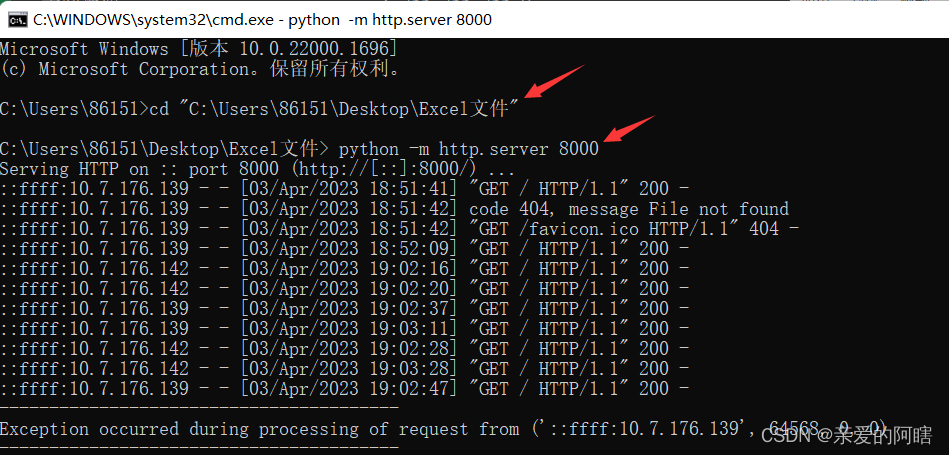
python开启局域网传输
python开启局域网传输 1.找自己的IP 在命令提示窗口输入:ipconfig <----找自己的IP地址 2.创建要传输文件的文件夹(只允许在该文件夹下访问传输) a.复制文件夹路径 b.在命令提示窗口cd打开新创建的文件夹 cd “C:\Users\86151\Desktop…...

病毒丨熊猫烧香病毒分析
作者丨黑蛋 一、病毒简介 病毒名称: 熊猫烧香 文件名称: 40fee2a4be91d9d46cc133328ed41a3bdf9099be5084efbc95c8d0535ecee496 文件格式: EXEx86 文件类型(Magic): MS-DOS executable 文件大小: 29.30KB SHA256&…...

SparkSQL学习——SparkSQL配置与文件的读取与保存
目录 一、添加依赖 二、配置log4j 三、spark提交jar包 四、读取文件 (一)加载数据 (二)保存数据 1.Parquet 2.json 3.CSV 4.MySql 5.hive on spark 6.IDEA的Spark中操作Hive 一、添加依赖 <properties><project.build.sourceEncoding>UTF-8</proje…...
, 322. 零钱兑换, 279.完全平方数)
随想录Day45--动态规划:70. 爬楼梯 (进阶), 322. 零钱兑换, 279.完全平方数
70爬楼梯这道题之前已经做过,是动态规划思想的入门,想要爬上第n层阶梯,看爬上n-1层的方法和n-2层的方法共有多少种,两个相加就是爬上n层阶梯的方法。这里扩展到每次可以爬k层,这样就是一个动态规划问题。因为每次可以爬…...

原理+案例,关于主从延迟,一篇文章给你讲明白!
前言 在生产环境中,为了满足安全性,高可用性以及高并发等方面的需求,基本上采用的MySQL数据库架构都是MHA、MGR等,最低也得是一主一从的架构,搭配自动切换脚本,实现故障自动切换。 上述架构都是通过集群主…...
QT开发笔记(Camera)
Camera 此章节例程适用于 Ubuntu 和正点原子 I.MX6U 开发板,不适用于 Windows(需要自行修改 才能适用 Windows,Windows 上的应用不在我们讨论范围)! 资源简介 正点原子 I.MX6U 开发板底板上有一路“CSI”摄像头接口。支持正点原…...
从C++的角度讲解C#容器
讲解C#容器的文章网上一搜一大把,作为一名C程序员如何高效学习C#容器呢,其实学语言如果能讲到这点就能触类旁通,举一反三,那效果是最好的问题市面上没有这样的书籍,那就跟着老白来一起从C的角度去讲解C#容器1.List<…...

React组件库实践:React + Typescript + Less + Rollup + Storybook
背景 原先在做低代码平台的时候,刚好有搭载React组件库的需求,所以就搞了一套通用的React组件库模版。目前通过这套模板也搭建过好几个组件库。 为了让这个模板更干净和通用,我把所有和低代码相关的代码都剔除了,只保留最纯粹的…...

c++ atomic
文章目录why atomic?sequentially consistent atomicRelaxed memory modelswhy atomic? 当我们有一片内存空间S,线程A正在往S里写数据,这个时候线程B突然往S中做了操作,导致线程A的操作结果变得不可预知(对线程A来说),这种情况换句话说叫做data race,我们一般的操作时上锁,在…...
要想孩子写作文没烦恼?建议家长这样做
说起语文学习,就不得不提作文。作为语文学习中的重中之重,作文写作一直是压在学生和家长身上的一块“心头大石”。发现很多孩子在写作文时,往往存在四大问题:写不出、不生动、流水账、太空洞。如今,孩子怕写作文&#…...
基于Python的高光谱图像分析教程
1、前言超光谱图像 (HSI) 分析因其在从农业到监控的各个领域的应用而成为人工智能 (AI) 研究的前沿领域之一。 该领域正在发表许多研究论文,这使它变得更加有趣! 和“对于初学者来说,在 HSI 上开始模式识别和机器学习是相当麻烦的”ÿ…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
