【C++】二叉搜索树+变身 = AVL树


目录
- 前言
- 一、AVL树
- 二、AVL树的实现
- 2.1 平衡因子
- 2.2 旋转处理
- 2.2.1 左单旋:插入新节点后单纯的右边高
- 2.2.2 右单旋:插入新节点后单纯的左边高
- 2.2.3 左右旋:插入新节点后不是单纯的左边高
- 2.2.4 右左旋:插入新节点后不是单纯的右边高
- 2.3 验证AVL树的平衡
- 三、完整代码
前言
本文仅适合了解二叉搜索树,但不了解AVL树底层原理的同学阅读哦。
本篇文章不会带你从头到尾实现AVL树,但会带你深入理解AVL树是怎么实现平衡的,怎么通过旋转变换实现保持平衡,以及实现平衡过程中的细节应该怎么处理等。
一、AVL树
前面的文章中我们分析过二叉搜索树的性能,得到的结果是理想情况下二叉搜索树的时间复杂度为O(LogN),但在极端情况下(即树蜕化为单边树时),这些操作的时间复杂度会退化为O(n),即使情况不那么极端,效率也不是特别高。
为了防止二叉搜索树出现一边偏高的情况,就需要想办法让二叉搜索树尽量保持平衡,所以两位苏联数学家(或称为俄罗斯数学家)G.M. Adelson-Velsky和E.M. Landis就发明了AVL树,其任何节点的两个子树的高度最大差别为1。
AVL树是具有一下性质的二叉搜索树:
- 其左右子树都是AVL树
- 左右子树高度差不超过1
二、AVL树的实现
本篇文章将沿用之前文章中Key-Value模型的代码,不再从底层开始实现,主要介绍在插入新节点后如何保持二叉搜索树的平衡问题。
2.1 平衡因子
如何保证AVL树的左右子树高度差不超过1?在AVL树的每个节点中存一个平衡因子,本文我们定义平衡因子 = 此节点右子树的高度 - 左子树的高度。
- 插入在左子树,平衡因子 - -
- 插入在右子树,平衡因子++
更新祖先节点的平衡因子时,我们首先需要找到祖先节点,因此每个节点中还需要增加一个指向父节点的指针。
按照我们的需求,其AVL树的节点可以定义为:
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//平衡因子//构造AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};
是否继续往上更新祖先节点的平衡因子,要看parent所在子树的高度是否发生变化。
插入新节点后其父节点的平衡因子有以下几种情况:
- parent的平衡因子 == 0
parent的平衡因子更新前是 -1 / 1,新节点插入在矮的那边,高度不变,不再往上更新 - parent的平衡因子 == 1 / -1
parent的平衡因子更新前是0,parent所在子树高度都变化了,需要往上更新 - parent的平衡因子 == 2 / -2
parent的平衡因子更新前是 -1 / 1,插入新节点后树不再平衡,需要旋转处理
pcur = new Node(kv);
if (parent->_kv.first > kv.first)//判断新节点应该插入左还是右
{parent->_left = pcur;
}
else
{parent->_right = pcur;
}
pcur->_parent = parent;//与父节点链接关系while (parent)//有可能更新到根节点去
{parent->_bf = parent->_left == pcur ? parent->_bf - 1 : parent->_bf + 1;if (parent->_bf == 0)//插入前后高度不变{break;}else if (parent->_bf == 1 || parent->_bf == -1){//高度变了,继续往上更新pcur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//插入节点后二叉树不平衡了,需要旋转处理}else{assert(false);//检测AVL树是否异常}
}
2.2 旋转处理
当二叉搜索树出现不平衡的情况时,需要旋转处理,对应插入后二叉搜索树的各种情况,主要有四种旋转的方式来保持平衡。
其中:
- h代表子树的高度,可以是0、1、2…
- 我们用能代表所有情况的四种类型的抽象图来研究旋转方式,单纯研究某几种情况没有意义
原则:
- 保持搜索树的性质
- 降低高度,控制平衡
2.2.1 左单旋:插入新节点后单纯的右边高
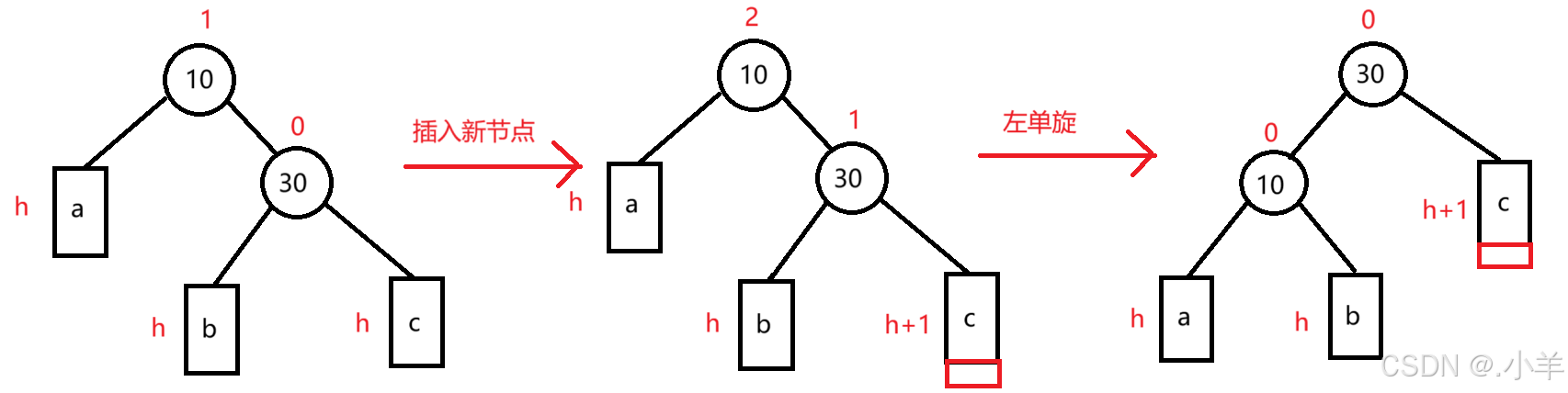
旋转处理过程中,我们主要关注三个节点(以上图为例):10(标记为
parent)、30(标记为subR)、b(标记为subLR)。
在旋转过程中,有以下几种情况需要考虑:
subR的左孩子可能存在,也可能不存在parent可能是根节点,也可能是子树。如果是根节点,旋转完成后,要更新根节点;如果是子树,可能是某个节点的左子树,也可能是右子树
//左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;//subRL是有可能为空的parent->_right = subRL;subR->_left = parent;Node* parentparent = parent->_parent;parent->_parent = subR;if (parentparent == nullptr)//subR有可能变成根{_root = subR;}else{if (parentparent->_left == parent){parentparent->_left = subR;}else{parentparent->_right = subR;}}subR->_parent = parentparent;if (subRL){subRL->_parent = parent;}parent->_bf = subR->_bf = 0;//更新平衡因子
}
旋转处理过程中主要是处理各节点的父节点指针的指向和平衡因子的更新。
2.2.2 右单旋:插入新节点后单纯的左边高
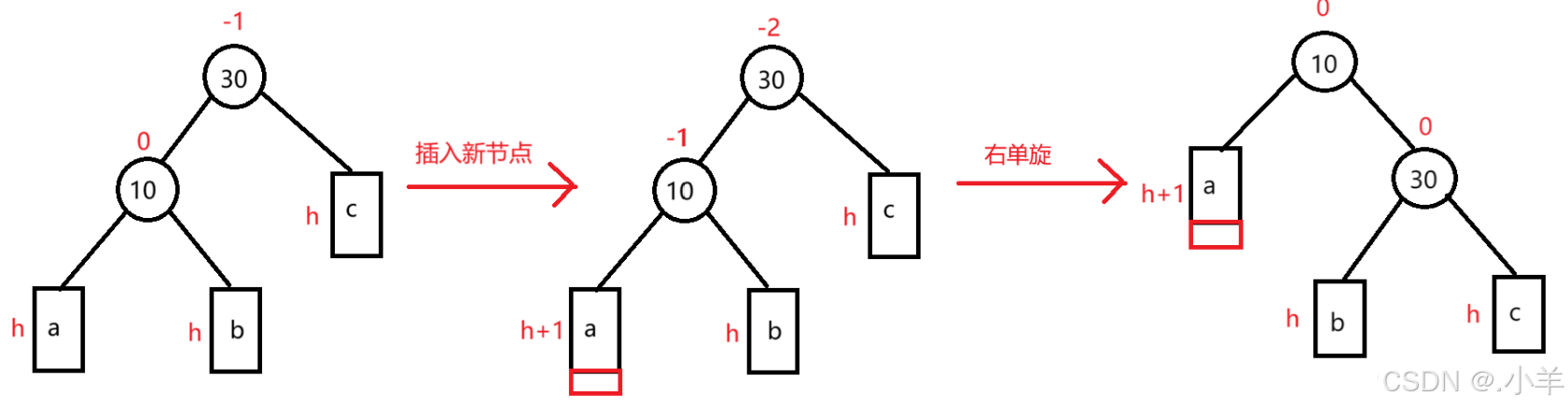
其处理方式和左单旋相似,可参考左单旋。
//右单旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;Node* parentparent = parent->_parent;parent->_parent = subL;if (parentparent == nullptr){_root = subL;}else{if (parentparent->_left == parent){parentparent->_left = subL;}else{parentparent->_right = subL;}}subL->_parent = parentparent;if (subLR){subLR->_parent = parent;}subL->_bf = parent->_bf = 0;
}
2.2.3 左右旋:插入新节点后不是单纯的左边高
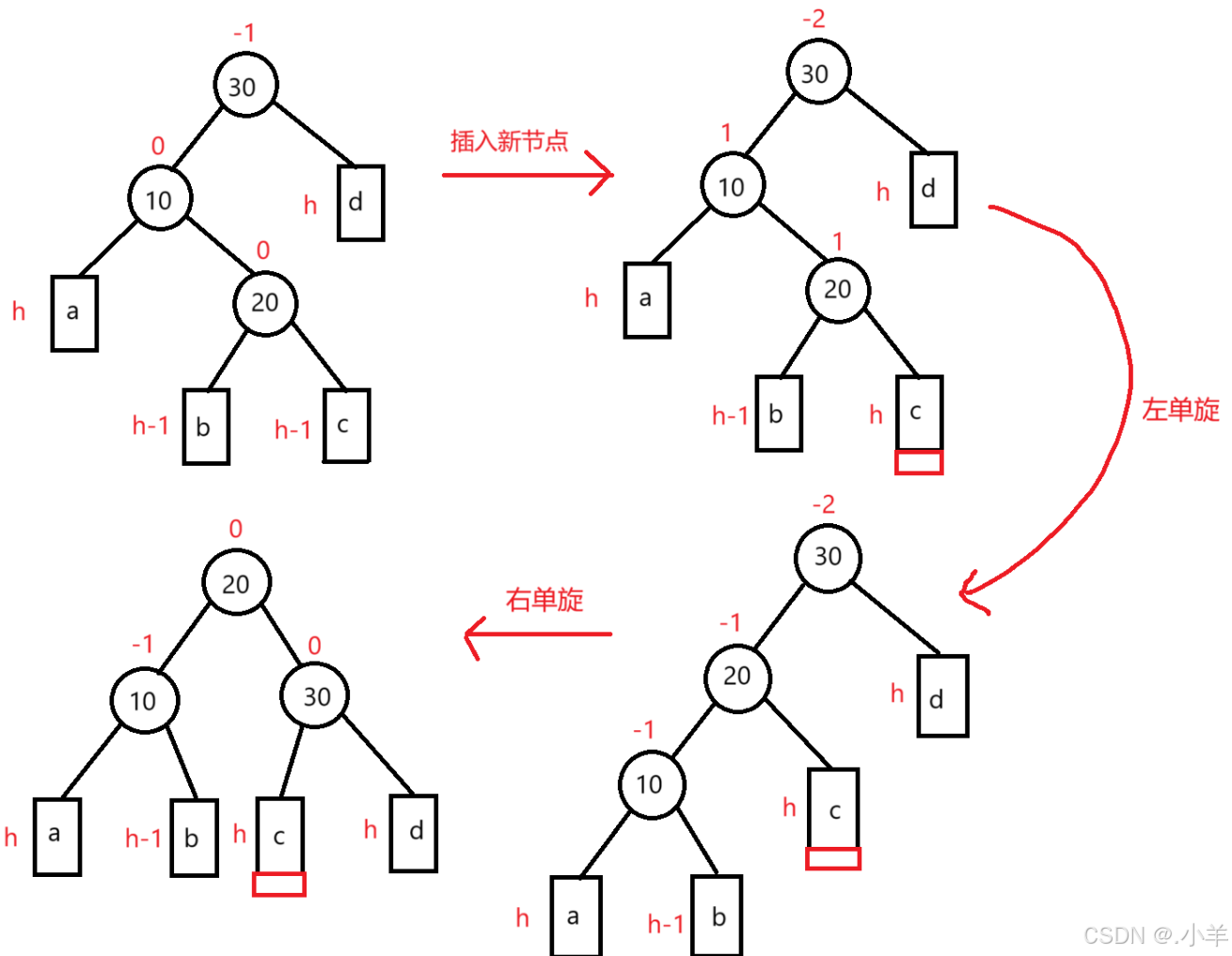
这种情况只用左旋或右旋只会原地打转,不能降低平衡。
我们需要先对subL进行左单旋,再对parent进行右单旋,最后更新平衡因子。
- 双旋后平衡因子的更新要根据插入新节点后
subLR的平衡因子来分情况讨论- 双旋最终结果是把
subLR推到最上面,让其平衡因子为0
//左右旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{assert(false);}
}
2.2.4 右左旋:插入新节点后不是单纯的右边高

可参考左右旋。
//右左旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}
旋转完成后,原parent为根的子树个高度降低,已经平衡,不需要再向上更新。
2.3 验证AVL树的平衡
我们可以分别计算出其左子树和右子树的高度,将其相减的值与节点中记录的平衡因子的值比较,看是否符合我们的预期。
int _Height(Node* root)
{if (root == nullptr){return 0;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}bool _isBalanceTree(Node* root)
{if (root == nullptr){return true;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);int bf = rightheight - leftheight;if (abs(bf) > 1){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _isBalanceTree(root->_left) && _isBalanceTree(root->_right);
}
三、完整代码
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:AVLTree() = default;AVLTree(const AVLTree<K, V>& t){_root = copy(t._root);}AVLTree<K, V>& operator=(AVLTree<K, V> t){swap(_root, t._root);return *this;}~AVLTree(){Destroy(_root);_root = nullptr;}bool Find(const K& key){Node* pcur = _root;while (pcur){if (key < pcur->_kv.first){pcur = pcur->_left;}else if (key > pcur->_kv.first){pcur = pcur->_right;}else{return true;}}return false;}bool Insert(const pair<K, V>& kv){//没有节点时需要单独处理if (_root == nullptr){_root = new Node(kv);return true;}Node* pcur = _root;Node* parent = nullptr;while (pcur){if (kv.first < pcur->_kv.first){parent = pcur;pcur = pcur->_left;}else if (kv.first > pcur->_kv.first){parent = pcur;pcur = pcur->_right;}else{return false;}}pcur = new Node(kv);if (parent->_kv.first > kv.first)//判断新节点应该插入左还是右{parent->_left = pcur;}else{parent->_right = pcur;}pcur->_parent = parent;//与父节点链接关系//更新平衡因子while (parent)//有可能更新到根节点去{parent->_bf = parent->_left == pcur ? parent->_bf - 1 : parent->_bf + 1;if (parent->_bf == 0)//插入前后高度不变{break;}else if (parent->_bf == 1 || parent->_bf == -1){//高度变了,继续往上更新pcur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//插入节点后二叉树不平衡了,需要旋转处理if (parent->_bf == 2 && pcur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && pcur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && pcur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && pcur->_bf == 1){RotateLR(parent);}break;//不管是哪种情况,旋转完后子树的高度没有变化,所以不再调整}else{assert(false);//检测AVL树是否异常}}return true;}void InOrder(){_InOrder(_root);cout << endl;}bool IsBalanceTree(){return _isBalanceTree(_root);}private://左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;//subRL是有可能为空的parent->_right = subRL;subR->_left = parent;Node* parentparent = parent->_parent;parent->_parent = subR;if (parentparent == nullptr)//subR有可能变成根{_root = subR;}else{if (parentparent->_left == parent){parentparent->_left = subR;}else{parentparent->_right = subR;}}subR->_parent = parentparent;if (subRL){subRL->_parent = parent;}parent->_bf = subR->_bf = 0;//更新平衡因子}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;Node* parentparent = parent->_parent;parent->_parent = subL;if (parentparent == nullptr){_root = subL;}else{if (parentparent->_left == parent){parentparent->_left = subL;}else{parentparent->_right = subL;}}subL->_parent = parentparent;if (subLR){subLR->_parent = parent;}subL->_bf = parent->_bf = 0;}//左右旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{assert(false);}}//右左旋void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}Node* copy(Node* root){if (root == nullptr){return nullptr;}Node* copynode = new Node(root->_kv);copynode->_left = copy(root->_left);copynode->_right = copy(root->_right);return copynode;}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}void _InOrder(Node* root){if (root == nullptr)//递归一定要有结束条件{return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}int _Height(Node* root){if (root == nullptr){return 0;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}bool _isBalanceTree(Node* root){if (root == nullptr){return true;}int leftheight = _Height(root->_left);int rightheight = _Height(root->_right);int bf = rightheight - leftheight;if (abs(bf) > 1){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _isBalanceTree(root->_left) && _isBalanceTree(root->_right);}private:Node* _root = nullptr;
};
本篇文章的分享就到这里了,如果您觉得在本文有所收获,还请留下您的三连支持哦~

相关文章:

【C++】二叉搜索树+变身 = AVL树
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 前言一、AVL树二、AVL树的实现2.1 平衡因子2.2 旋转处理2.2.1 左单旋:插入新节点后单纯的右边高2.2.2 …...

Flutter String 按 ,。分割
在 Flutter 中,如果你想将一个字符串按特定的字符(例如中文逗号 , 和英文句号 .)进行分割,可以使用 Dart 语言的字符串处理功能。具体来说,你可以使用 split 方法,并传入一个正则表达式来匹配这…...

Redis: 集群高可用之MOVED转向和ASK转向解决方案
MOVED转向 1 ) 问题描述 在客户端操作Redis集群的时候 MOVED转向 或 MOVED错误是经常遇到的一类问题我们先连入集群:$ /usr/local/redis/bin/redis-cli -a 123456 -h 192.168.10.101 -p 6371之前在Redis中存储过一些数据,比如下面的情况,当输…...
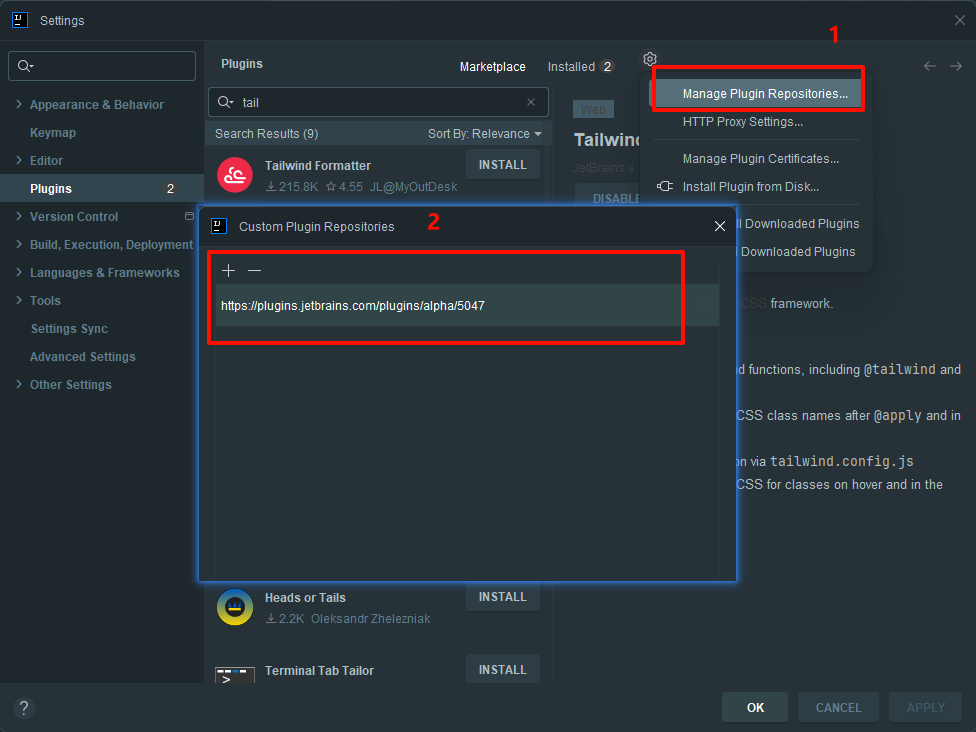
idea插件市场安装没反应
https://plugins.jetbrains.com/idea重启后还是不行那就...

数据结构之排序(5)
摘要:本文主要讲各种排序算法,注意它们的时间复杂度 概念 将各元素按关键字递增或递减排序顺序重新排列 评价指标 稳定性: 关键字相同的元素经过排序后相对顺序是否会改变 时间复杂度、空间复杂度 分类 内部排序——数据都在内存中 外部排序——…...

R包的安装、加载以及如何查看帮助文档
0x01 如何安装R包 一、通过R 内置函数安装(常用) 1.安装CRAN的R包 install.packages()是一个用于安装 R 包的重要函数。 语法:install.packages(pkgs, repos getOption("repos"),...) 其中: pkgs:要安…...

【YOLO学习】YOLOv3详解
文章目录 1. 网络结构1.1 结构介绍1.2 改进 2. 训练与测试过程3. 总结 1. 网络结构 1.1 结构介绍 1. 与 YOLOv2 不同的是,YOLOv3 在 Darknet-19 里加入了 ResNet 残差连接,改进之后的模型叫 Darknet-53。在 ImageNet上 实验发现 Darknet-53 相对于 ResN…...

JDK1.0主要特性
JDK 1.0,也被称为Java 1,是Java编程语言的第一个正式版本,由Sun Microsystems公司在1996年发布。JDK 1.0的发布标志着Java作为一种编程语言和平台的正式诞生,它带来了许多创新的概念和特性,对后来的软件开发产生了深远…...
)
CSS基础-盒子模型(三)
9、CSS盒子模型 9.1 CSS常用长度单位 1、px:像素; 2、em:相对元素font-size的倍数; 3、rem:相对根字体的大小,html标签即是根; 4、%:相对于父元素进行计算。 注意:CSS样…...

深度学习中的损失函数详解
深度学习中的损失函数详解 文章目录 深度学习中的损失函数详解损失函数的基础概念常见的损失函数类型及应用场景回归问题的损失函数分类问题的损失函数自定义损失函数 如何选择合适的损失函数?损失函数在深度学习中的应用 在深度学习的世界中,损失函数&a…...

系统架构设计师-下午案例题(2022年下半年)
1.试题-(共25分):阅读以下关于软件架构设计与评估的叙述在答题纸上回答问题1和问题2。 【说明】某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提…...
高级图片编辑器Photopea
什么是 Photopea ? Photopea 是一款免费的在线工具,用于编辑光栅和矢量图形,支持PSD、AI 和 Sketch文件。 功能上,Photopea 和 老苏之前介绍的 miniPaint 比较像 文章传送门:在线图片编辑器miniPaint 支持的格式 复杂…...

详解zookeeper四字命令
ZooKeeper 的四字命令(Four-Letter Words, 4LW)是一组简单的管理和监控命令,方便运维人员快速获取 ZooKeeper 集群和节点的运行状态。这些命令通常用于健康检查、性能监控、节点配置查看等操作。通过这些命令,可以轻松获取关于 Zo…...

docker 进入容器运行命令
要进入正在运行的Docker容器并在其中执行命令,你可以使用docker exec命令。以下是具体步骤和示例: 1. 查看正在运行的容器 首先,确认你的容器正在运行,可以使用以下命令查看所有运行中的容器: docker ps2. 进入容器…...

一行 Python 代码能实现什么丧心病狂的功能?圣诞树源代码
手头有 109 张头部 CT 的断层扫描图片,我打算用这些图片尝试头部的三维重建。基础工作之一,就是要把这些图片数据读出来,组织成一个三维的数据结构(实际上是四维的,因为每个像素有 RGBA 四个通道)。 这个…...

mit6824-01-MapReduce详解
文章目录 MapReduce简述编程模型执行流程执行流程排序保证Combiner函数Master数据结构 容错性Worker故障Master故障 性能提升定制分区函数局部性执行缓慢的worker(slow workers) 常见问题总结回顾参考链接 MapReduce简述 MapReduce是一个在多台机器上并行计算大规模数据的软件架…...

在Docker中运行微服务注册中心Eureka
1、Docker简介: 作为开发者,经常遇到一个头大的问题:“在我机器上能运行”。而将SpringCloud微服务运行在Docker容器中,避免了因环境差异带来的兼容性问题,能够有效的解决此类问题。 通过Docker,开发者可…...

白话进程>线程>协程
文章目录 概述进程线程协程区别与联系 举个栗子进程例子线程例子协程例子区别与联系的具体体现 代码示例进程例子线程例子协程(Goroutine)例子 概述 进程、线程和协程是计算机科学中的基本概念,它们在操作系统和并发编程中扮演着重要角色。以…...
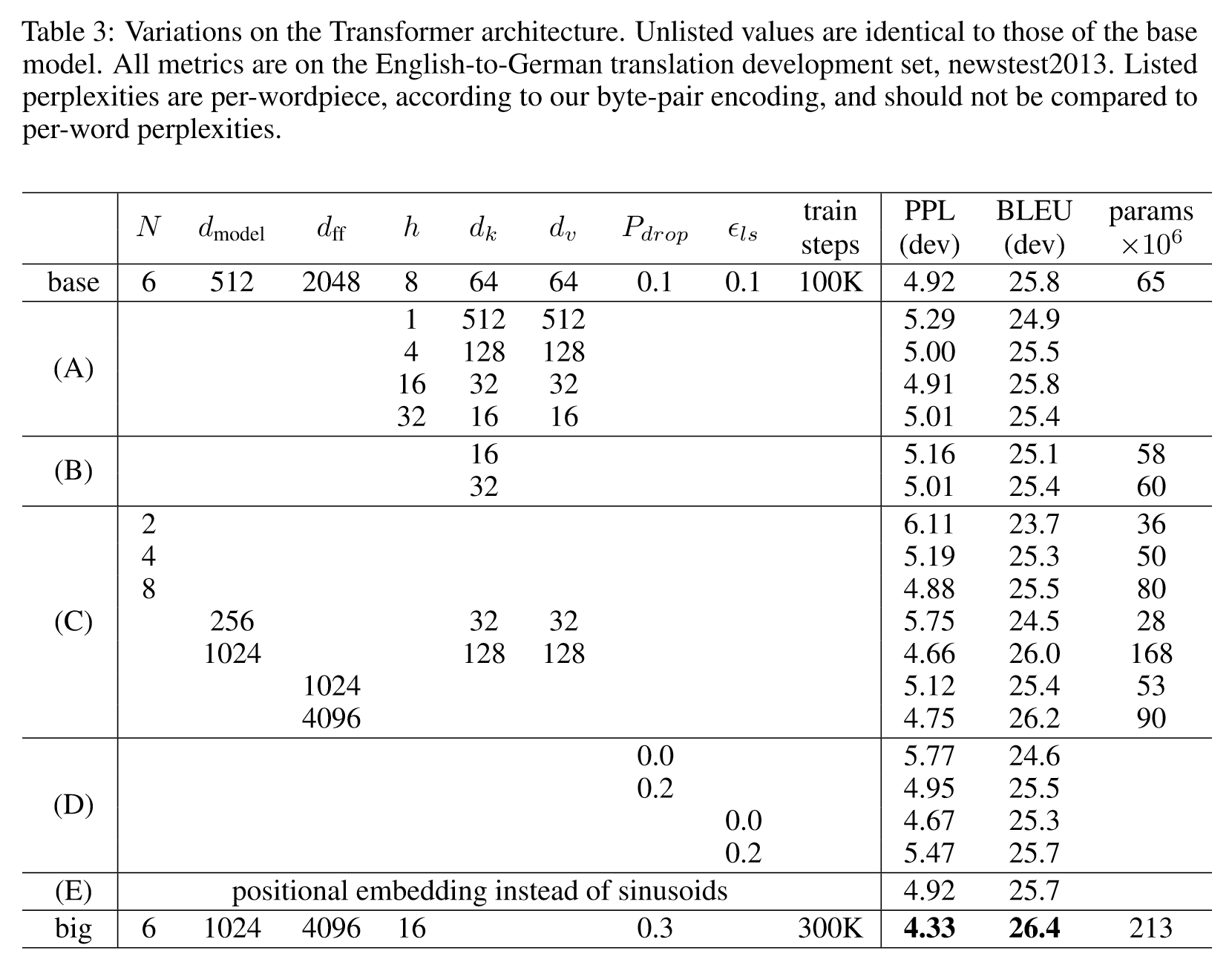
论文阅读:Attention is All you Need
Abstract 贡献: 提出了Transformer,完全基于注意力机制,摒弃了循环和卷积网络。 结果: 本模型在质量上优于现有模型,同时具有更高的并行性,并且显著减少了训练时间。 1. Introduction long short-term …...

【Linux 】文件描述符fd、重定向、缓冲区(超详解)
目录 编辑 系统接口进行文件访问 open 接口介绍 文件描述符fd 重定向 缓冲区 1、缓冲区是什么? 2、为什么要有缓冲区? 3、怎么办? 我们先来复习一下,c语言对文件的操作: C默认会打开三个输入输出流…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
