代码随想录 | Day28 | 回溯算法:组合组合总和III
代码随想录 | Day28 | 回溯算法:组合&&组合总和III
关于这个章节,大家最好是对递归函数的理解要比较到位,听着b站视频课可能呢才舒服点,可以先去搜一搜关于递归函数的讲解,理解,再开始这个章节会比较好一些
我觉得回溯就是对传入递归函数的参数加加减减,加了的减掉,减了的加上
主要学习内容:
组合题目的模板
77.组合
[77. 组合 - 力扣(LeetCode)](https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/description/)
解法思路:
首先,把问题转换为树形结构,树的每一层的各个结点都是由本层逻辑的for循环产生的,树的深度是由我们所求集合的大小决定的。
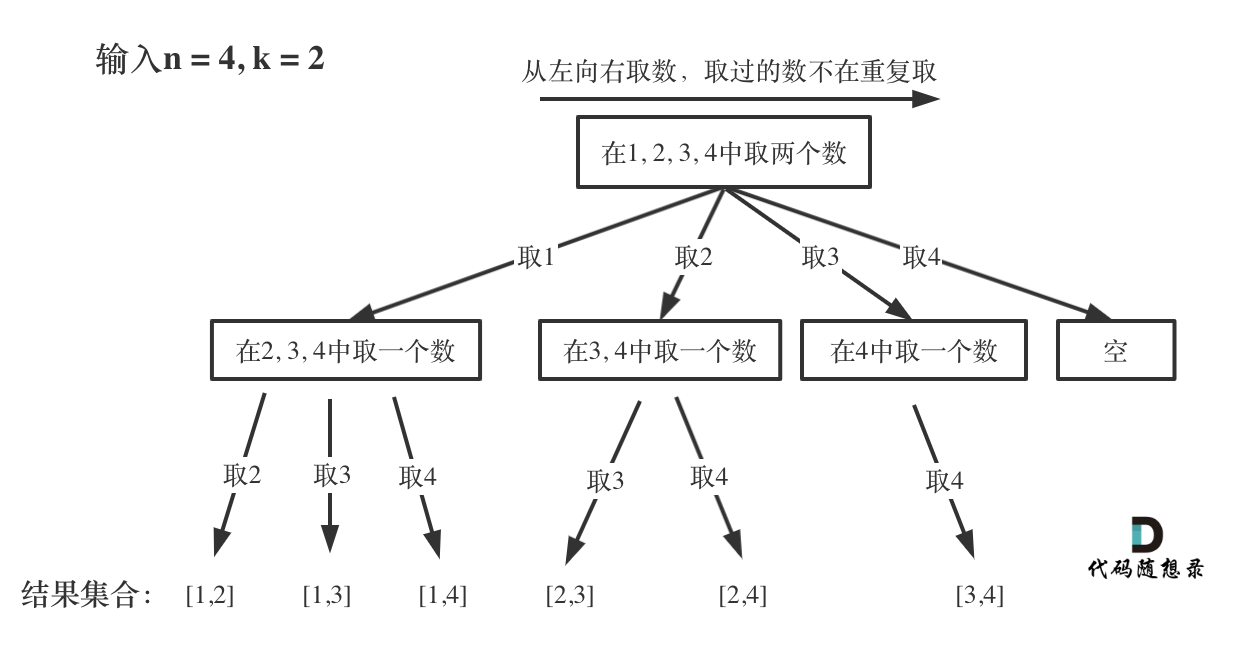
我们在第一层取出一个数字,第一层就是 1 ,2 ,3 ,4
第二层从剩余的集合中取出一个数字,那就是 [1,2] [1,3] [1,4] …
而我们集合大小为2,那么就只有这两层,树的深度也就这两层
而我们选完[1,2]怎么返回[1]的时候去选择[1,3]呢?
这时候就是回溯算法,回溯就是恢复你选择之前的状态,让你去选择另外一个,本质上是穷举的思想
1.函数参数和返回值
vector<vector<int>> res;
void backtracking(vector<int> path,int n,int k,int index)
res存放结果,path是当前已经收集的组合,n,k不必说,index表示我们已经选到哪个数字了,防止出现重复的组合
2.终止条件
我们当前收集的集合大小等于要求的大小就收集到最后的结果集中,然后返回,这也是能够控制树的深度只有两层的原因
if(path.size()==k)
{res.push_back(path);return;
}
3.本层代码逻辑
其实最难理解的就是for循环部分。
由于题目要求的是组合,我们只要防止重复,所以引入index,让index之前的已经选过的数不再出现,比如第一层选了2之后,index会让1和2不再出现,只会出现3,4,不会同时出现[1,2]和[2,1]这两个组合了
对for的理解可以脑补一下,举例比如选了1之后,本层的递归函数index是1
进入for循环,传入的先是2,在树的下一层,产生了[1,2]组合,大小满足2,结束递归返回上层,上层将2弹出,继续下一次循环,传入的就是3,产生了[1,3],以此类推
需要注意的是不要写成index+1,这个是错误的,会出现:在你选完第一层的数字后,不管你第一层选的数是多少,第二层都是从2开始的
错误案例
n=4,k=2

最后递归函数返回来以后,把咱压入的元素再弹出就好
for(int i=index;i<=n;i++)
{path.push_back(i);backtracking(path,n,k,i+1);//注意不是index+1path.pop_back();//回溯,恢复现场
}
完整代码:
class Solution {
public:vector<vector<int>> res; void backtracking(vector<int> path,int n,int k,int index){if(path.size()==k){res.push_back(path);return;}for(int i=index;i<=n;i++){path.push_back(i);backtracking(path,n,k,i+1);//注意不是index+1path.pop_back();}}vector<vector<int>> combine(int n, int k) {vector<int> path;backtracking(path,n,k,1);return res;}
};
优化
注意代码中i,就是for循环里选择的起始位置,可以循环的次数少一点。(大家可以看代码随想录中的)
for (int i = startIndex; i <= n; i++) {
接下来看一下优化过程如下:
- 已经选择的元素个数:path.size();
- 所需需要的元素个数为: k - path.size();
- 列表中剩余元素(n-i) >= 所需需要的元素个数(k - path.size())
- 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
从2开始搜索都是合理的,可以是组合[2, 3, 4]。
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
216.组合总和III
216. 组合总和 III - 力扣(LeetCode)
思路:
思路和上一题一模一样,就是上一题给定的n换成了9,然后多了一个加和的操作
加和的操作你可以等到有3个数以后再加起来进行比较,也可以在递归的过程中累加并且比较
1.函数返回值和参数
vector<vector<int>> res;
void backtracking(vector<int> path,int k,int sum,int n,int index)
res记录结果
path收集当前组合
k组合大小
n总和值
sum当前集合的总和
index从哪个数开始
2.终止条件
当前总和已经大于n了,没必要再递归了
如果大小等于k并且加起来等于n,收集结果,不等于n直接返回
if(sum>n)return ;
if(path.size()==k)
{if(sum==n)res.push_back(path);return;
}
3.本层逻辑
优化的思路一样的直接套用了
和上一题不一样的就是多加了一个总和值sum
让sum加上我们压入path的值i传入下层即可,下层函数会在终止条件进行比较。
for(int i=index;i<=9-(k-path.size())+1;i++)
{path.push_back(i);backtracking(path,k,sum+i,n,i+1);//也可以写成 递归函数前写sum+=i,递归函数后写sum-=i,也可以写在递归函数参数中,比如我这样的path.pop_back();//回溯过程
}
完整代码:
class Solution {
public:vector<vector<int>> res;void backtracking(vector<int> path,int k,int sum,int n,int index){if(sum>n)return ;if(path.size()==k){if(sum==n)res.push_back(path);return;}for(int i=index;i<=9-(k-path.size())+1;i++){path.push_back(i);backtracking(path,k,sum+i,n,i+1);path.pop_back();}}vector<vector<int>> combinationSum3(int k, int n) {vector<int> path;backtracking(path,k,0,n,1);return res;}
};
相关文章:

代码随想录 | Day28 | 回溯算法:组合组合总和III
代码随想录 | Day28 | 回溯算法:组合&&组合总和III 关于这个章节,大家最好是对递归函数的理解要比较到位,听着b站视频课可能呢才舒服点,可以先去搜一搜关于递归函数的讲解,理解,再开始这个章节会比…...

【重学 MySQL】四十五、数据库的创建、修改与删除
【重学 MySQL】四十五、数据库的创建、修改与删除 一条数据存储的过程数据输入数据验证数据处理数据存储数据持久化反馈与日志注意事项 标识符命名规则基本规则长度限制保留字与特殊字符命名建议示例 MySQL 中的数据类型创建数据库创建数据库时指定字符集和排序规则 查看数据库…...

STM32驱动直流电机
stm32通过PWM控制直流电机的方向和速度。 小直流电机需要几百毫安的电流,单片机只能提供几毫安的电流。电机内线圈转动时切割磁感线以及电机内转子线圈的电感效应都会产生反电动势,损坏芯片。 电机驱动芯片能够作为STM32驱动电机的帮手。 SLEEP暂停工作…...

【C++】二叉搜索树+变身 = AVL树
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 前言一、AVL树二、AVL树的实现2.1 平衡因子2.2 旋转处理2.2.1 左单旋:插入新节点后单纯的右边高2.2.2 …...

Flutter String 按 ,。分割
在 Flutter 中,如果你想将一个字符串按特定的字符(例如中文逗号 , 和英文句号 .)进行分割,可以使用 Dart 语言的字符串处理功能。具体来说,你可以使用 split 方法,并传入一个正则表达式来匹配这…...

Redis: 集群高可用之MOVED转向和ASK转向解决方案
MOVED转向 1 ) 问题描述 在客户端操作Redis集群的时候 MOVED转向 或 MOVED错误是经常遇到的一类问题我们先连入集群:$ /usr/local/redis/bin/redis-cli -a 123456 -h 192.168.10.101 -p 6371之前在Redis中存储过一些数据,比如下面的情况,当输…...
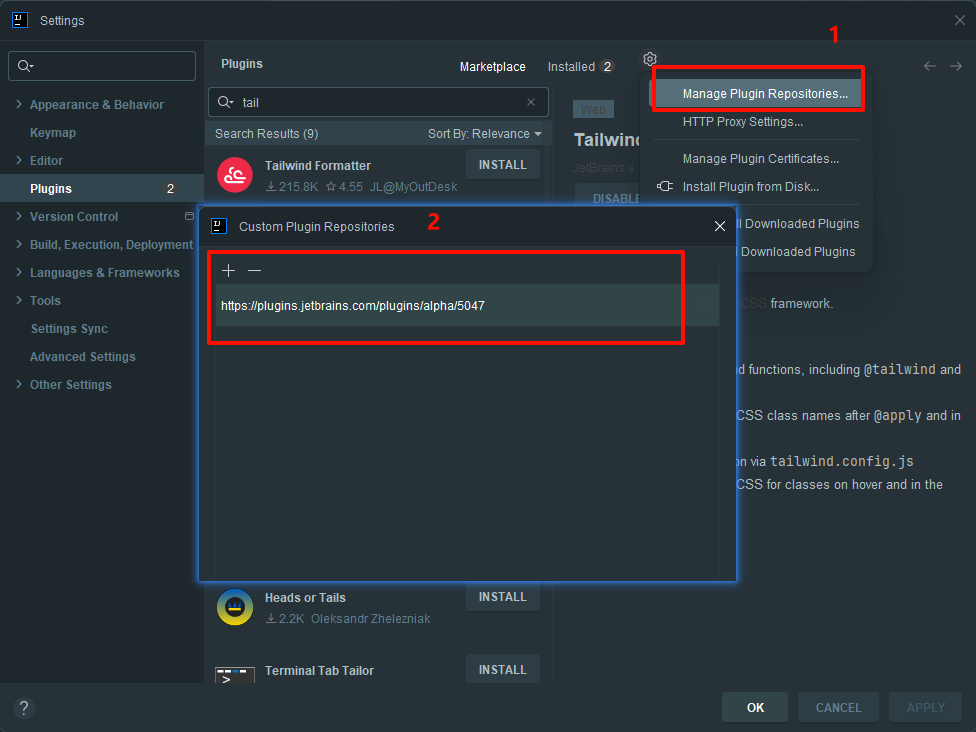
idea插件市场安装没反应
https://plugins.jetbrains.com/idea重启后还是不行那就...

数据结构之排序(5)
摘要:本文主要讲各种排序算法,注意它们的时间复杂度 概念 将各元素按关键字递增或递减排序顺序重新排列 评价指标 稳定性: 关键字相同的元素经过排序后相对顺序是否会改变 时间复杂度、空间复杂度 分类 内部排序——数据都在内存中 外部排序——…...

R包的安装、加载以及如何查看帮助文档
0x01 如何安装R包 一、通过R 内置函数安装(常用) 1.安装CRAN的R包 install.packages()是一个用于安装 R 包的重要函数。 语法:install.packages(pkgs, repos getOption("repos"),...) 其中: pkgs:要安…...

【YOLO学习】YOLOv3详解
文章目录 1. 网络结构1.1 结构介绍1.2 改进 2. 训练与测试过程3. 总结 1. 网络结构 1.1 结构介绍 1. 与 YOLOv2 不同的是,YOLOv3 在 Darknet-19 里加入了 ResNet 残差连接,改进之后的模型叫 Darknet-53。在 ImageNet上 实验发现 Darknet-53 相对于 ResN…...

JDK1.0主要特性
JDK 1.0,也被称为Java 1,是Java编程语言的第一个正式版本,由Sun Microsystems公司在1996年发布。JDK 1.0的发布标志着Java作为一种编程语言和平台的正式诞生,它带来了许多创新的概念和特性,对后来的软件开发产生了深远…...
)
CSS基础-盒子模型(三)
9、CSS盒子模型 9.1 CSS常用长度单位 1、px:像素; 2、em:相对元素font-size的倍数; 3、rem:相对根字体的大小,html标签即是根; 4、%:相对于父元素进行计算。 注意:CSS样…...

深度学习中的损失函数详解
深度学习中的损失函数详解 文章目录 深度学习中的损失函数详解损失函数的基础概念常见的损失函数类型及应用场景回归问题的损失函数分类问题的损失函数自定义损失函数 如何选择合适的损失函数?损失函数在深度学习中的应用 在深度学习的世界中,损失函数&a…...

系统架构设计师-下午案例题(2022年下半年)
1.试题-(共25分):阅读以下关于软件架构设计与评估的叙述在答题纸上回答问题1和问题2。 【说明】某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提…...
高级图片编辑器Photopea
什么是 Photopea ? Photopea 是一款免费的在线工具,用于编辑光栅和矢量图形,支持PSD、AI 和 Sketch文件。 功能上,Photopea 和 老苏之前介绍的 miniPaint 比较像 文章传送门:在线图片编辑器miniPaint 支持的格式 复杂…...

详解zookeeper四字命令
ZooKeeper 的四字命令(Four-Letter Words, 4LW)是一组简单的管理和监控命令,方便运维人员快速获取 ZooKeeper 集群和节点的运行状态。这些命令通常用于健康检查、性能监控、节点配置查看等操作。通过这些命令,可以轻松获取关于 Zo…...

docker 进入容器运行命令
要进入正在运行的Docker容器并在其中执行命令,你可以使用docker exec命令。以下是具体步骤和示例: 1. 查看正在运行的容器 首先,确认你的容器正在运行,可以使用以下命令查看所有运行中的容器: docker ps2. 进入容器…...

一行 Python 代码能实现什么丧心病狂的功能?圣诞树源代码
手头有 109 张头部 CT 的断层扫描图片,我打算用这些图片尝试头部的三维重建。基础工作之一,就是要把这些图片数据读出来,组织成一个三维的数据结构(实际上是四维的,因为每个像素有 RGBA 四个通道)。 这个…...

mit6824-01-MapReduce详解
文章目录 MapReduce简述编程模型执行流程执行流程排序保证Combiner函数Master数据结构 容错性Worker故障Master故障 性能提升定制分区函数局部性执行缓慢的worker(slow workers) 常见问题总结回顾参考链接 MapReduce简述 MapReduce是一个在多台机器上并行计算大规模数据的软件架…...

在Docker中运行微服务注册中心Eureka
1、Docker简介: 作为开发者,经常遇到一个头大的问题:“在我机器上能运行”。而将SpringCloud微服务运行在Docker容器中,避免了因环境差异带来的兼容性问题,能够有效的解决此类问题。 通过Docker,开发者可…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
