pytorch版本和cuda版本不匹配问题
文章目录
- 🌕问题:Python11.8安装pytorch11.3失败
- 🌕CUDA版本和pytorch版本的关系
- 🌕安装Pytorch2.0.0
- 🌙pip方法
- 🌙cuda方法
🌕问题:Python11.8安装pytorch11.3失败
🌕CUDA版本和pytorch版本的关系
+-------+-----------------------------------------+
| CUDA | Supported PyTorch Versions |
+-------+-----------------------------------------+
| 11.8 | 2.0.0 |
| 11.7 | 2.0.0, 1.13.1, 1.13.0 |
| 11.6 | 1.13.1, 1.13.0, 1.12.1, 1.12.0 |
| 11.3 | 1.12.0, 1.12.1, 1.11.0, 1.10.1, 1.10.0, |
| | 1.9.1, 1.9.0, 1.8.1 |
| 11.1 | 1.10.0, 1.9.1, 1.9.0, 1.8.2, 1.8.1, |
| | 1.8.0 |
| 11.0 | 1.7.1, 1.7.0 |
| 10.2 | 1.12.0, 1.12.1, 1.11.0, 1.10.1, 1.10.0, |
| | 1.9.1,1.9.0, 1.8.2, 1.8.1, 1.8.0, 1.7.1,|
| | 1.7.0, 1.6.0, 1.5.1, 1.5.0 |
| 10.1 | 1.8.1, 1.7.1, 1.7.0, 1.6.0, 1.5.1, |
| | 1.5.0, 1.4.0 |
| 10.0 | 1.2.0, 1.1.0, 1.0.1, 1.0.0 |
| 9.2 | 1.7.1, 1.7.0, 1.6.0, 1.5.1, 1.5.0, |
| | 1.4.0, 1.2.0 |
| 9.0 | 1.1.0, 1.0.1, 1.0.0 |
| 8.0 | 1.0.0 |
+-------+-----------------------------------------+
发现cuda11.8支持pytorch2.0.0
🌕安装Pytorch2.0.0
官网:https://pytorch.org/get-started/previous-versions/
🌙pip方法
# CUDA 11.8
pip install torch==2.0.0 torchvision==0.15.1 torchaudio==2.0.1 --index-url https://download.pytorch.org/whl/cu118

安装成功。
🌙cuda方法
# CUDA 11.8
conda install pytorch==2.0.0 torchvision==0.15.0 torchaudio==2.0.0 pytorch-cuda=11.8 -c pytorch -c nvidia
相关文章:

pytorch版本和cuda版本不匹配问题
文章目录 🌕问题:Python11.8安装pytorch11.3失败🌕CUDA版本和pytorch版本的关系🌕安装Pytorch2.0.0🌙pip方法🌙cuda方法 🌕问题:Python11.8安装pytorch11.3失败 🌕CUDA版…...

Vue/组件的生命周期
这篇文章借鉴了coderwhy大佬的Vue生命周期 在Vue实例化或者创建组件的过程中 内部涉及到一系列复杂的阶段 每一个阶段的前后时机都可能对应一个钩子函数 以下是我根据coderwhy大佬文章对于每一个阶段的一些看法 1.过程一 首先实例化Vue或者组件 在实例化之前 会对应一个钩子函…...

【Nacos架构 原理】内核设计之Nacos寻址机制
文章目录 前提设计内部实现单机寻址文件寻址地址服务器寻址 前提 对于集群模式,集群内的每个Nacos成员都需要相互通信。因此这就带来一个问题,该以何种方式去管理集群内部的Nacos成员节点信息,即Nacos内部的寻址机制。 设计 要能够感知到节…...
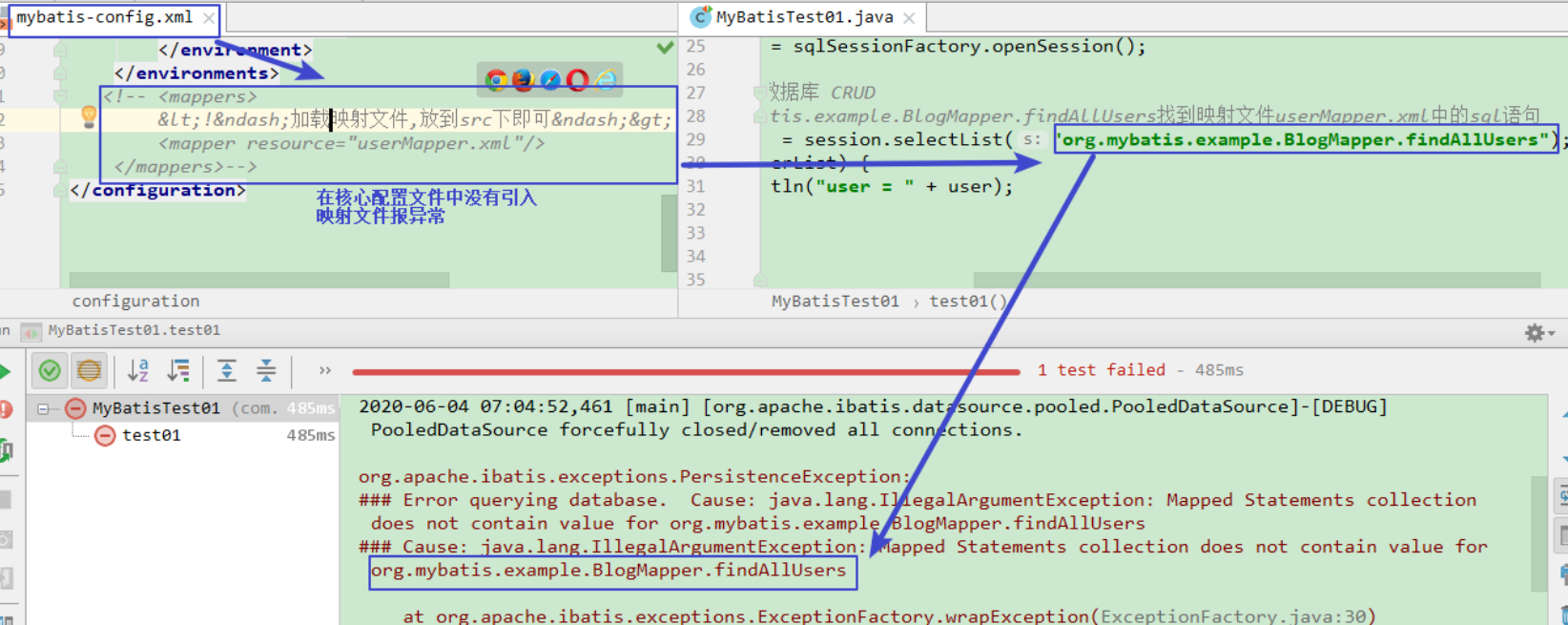
入门案例:mybatis流程,核心,常见错误
入门案例:mybatis执行流程分析 说明: 1.第一步:是从核心配置文件mybatis-config.xml中构建SqlSessionFactory对象,由于核心配置文件mybatis-config.xml中关联了映射文件UserMapper.xml,所以在SqlSessionFactory中也存在映射文件的…...

C++ | Leetcode C++题解之第456题132模式
题目: 题解: class Solution { public:bool find132pattern(vector<int>& nums) {int n nums.size();vector<int> candidate_i {nums[0]};vector<int> candidate_j {nums[0]};for (int k 1; k < n; k) {auto it_i upper_…...

自然语言处理问答系统
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Python的几个高级特性
引言 Python是一种功能强大的编程语言,它简洁的语法和强大的库支持使其成为数据科学和机器学习领域的热门选择。在Python的高级特性中,生成器、迭代器、闭包、装饰器和内置高阶函数是实现高效、优雅代码的关键。本文将逐一介绍这些特性,并提…...

【颜色平衡树 / E】
题目 思路 DFS暴力 60分 代码 #include <bits/stdc.h> using namespace std; const int N 5010; const int M 5010; int h[N], e[M], ne[M], idx; int c[N], f; int ans; void add(int a, int b) // 添加一条边a->b {e[idx] b, ne[idx] h[a], h[a] idx ; } …...

滑动窗口--(中篇)
将X减到0的最小操作数 给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。 如果可以将 x 恰好 减到 0 ,返…...

Java性能调优:实战技巧与最佳实践
引言 Java作为企业级应用开发的首选语言之一,其性能直接影响到系统的响应速度和用户体验。性能调优是一项复杂的工作,涉及多个层面的知识和技术。本文将通过具体的示例,探讨一些常见的性能调优技巧及最佳实践。 1. 了解你的应用程序 示例&…...

排版套料系统设计说明
先上效果图 项目地址 1.产品介绍 产品名称:StreamFit 智能排版套料系统 主要功能: 智能排版优化 功能描述:StreamFit 利用先进的算法技术,自动对各类材料(如布料、金属板材、纸张等)进行高效排版布局&am…...

算法修炼之路之二分查找
目录 一:三大二分介绍及模板 1.普通二分 2.查找左右边界的二分及模板 二:LeetCode OJ练习 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 6.第六题 一:三大二分介绍及模板 1.普通二分 这里通过一道题来引出普通二分及模板 LeetCode_704 二分查找 画图分析: 具体代…...

OpenAI预计明年将推出“代理”系统
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

每日OJ题_牛客_重排字符串_贪心_C++_Java
目录 牛客_重排字符串_贪心 题目解析 C代码 Java代码 牛客_重排字符串_贪心 重排字符串 (nowcoder.com) 描述: 小红拿到了一个只由小写字母组成的字符串。她准备把这个字符串重排(只改变字母的顺序,不改变数量) …...

Python 进阶部分详细整理
1. 面向对象编程(OOP) 面向对象编程 (OOP) 是一种通过将程序中的数据和功能封装为对象的编程范式。OOP 基于四个核心概念:类与对象、继承、封装与多态。 类与对象 类(Class):类是创建对象的蓝图或模板。它…...

[ RK3566-Android11 ] 关于移植 RK628F 驱动以及后HDMI-IN图像延迟/无声等问题
问题描述 由前一篇文章https://blog.csdn.net/jay547063443/article/details/142059700?fromshareblogdetail&sharetypeblogdetail&sharerId142059700&sharereferPC&sharesourcejay547063443&sharefromfrom_link,移植HDMI-IN部分驱动后出现&a…...

【黑马点评】 使用RabbitMQ实现消息队列——2.使用RabbitMQ监听秒杀下单
2 使用RabbitMQ实现消息队列 2.1 修改\hm-dianping\pom.xmlpom.xml文件 添加RabbitMQ的环境 <!-- RabbitMQ--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </depe…...
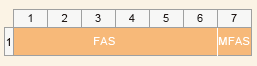
业务封装与映射 -- OTUk/ODUk/OPUk开销帧结构
开销是为了保证净荷正常、灵活传送所必须附加的供网络运行、管理和维护(OAM)使用的字节。 OTN电层开销包括OTUk开销、ODUk开销、OPUk开销、OTUCn开销、ODUCn开销、OPUCn开销和帧对齐开销。 SM开销属于OTU开销,占用3个字节;PM开销…...

Vim基本用法
Vim用法 一、基本模式 1. 普通模式(Normal Mode) 移动光标 基本移动:使用方向键(h左移、j下移、k上移、l右移),也可以使用 H(移到屏幕顶部)、M(移到屏幕中间ÿ…...

python 实现Tarjan 用于在有向图中查找强连通分量的算法
Tarjan 用于在有向图中查找强连通分量的算法介绍 Tarjan算法是一种用于在有向图中查找强连通分量的高效算法,由Robert Tarjan在1972年提出。强连通分量是指在有向图中,如果从顶点u到顶点v以及从顶点v到顶点u都存在一条路径,那么顶点u和顶点v…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
