【判断推理】逻辑基础
1.1 命题
- 用语言、符号或者式子表达的,可以判断真假的陈述句称为命题,一般写为 若p,则q
- 真命题:判断为真的语句
- 假命题:判断为假的语句
eg1:小张是中国人(若是小张,则是中国人)
eg2:明天是星期六(若是明天,则是星期三)


- 对于真假判断,主要是关注啥为假话


小试牛刀
1.2 复合命题
- 复合命题:由简单命题用联结词联结而成的命题
-
联言命题(且)
联言命题是反映事物的若干种情况或者性质同时存在的命题,由逻辑连接词“并且”连接,写成p且q
eg1:小莫的计算机配置合理并且价格低廉。
eg2:这项水利工程使附近几个县的农田收益,且为这一地区的小工业提供了动力。
eg3:生也有涯,知也无涯。


-
选言命题(或者或者、要么要么)
选言命题是反映事物的若干种情况或者性质至少有一种存在的命题。分为相容选言命题和不相容选言命题。由逻辑联结词“或者”或“要么”连接,写成 p或q、要么p要么q
eg1:或者明天是星期五,或者明天是星期六
eg2:小张学过英语或者法语
eg3:要么生,要么死





-
假言命题(如果那么、只要就、否则、一就、只有才、除非否则)
假言命题是陈述某一事物情况是另一件事物情况的条件的命题,假言命题也称条件命题
eg1:如果小李是犯罪嫌疑人,那么小李有犯罪动机
eg2:如果在淀粉溶液里加入碘酒,那么淀粉溶液会变蓝
eg3:只有水分充足,庄稼才能茁壮生长
eg4:一个代数方程能得到根的计算公式当且仅当这个代数方程的次数不超过四






-

1.3 模态命题(可能必然)
- 模态命题是陈述事物情况的必然性或可能性的命题
eg1:违反客观规律必然受到惩罚
eg2:改善生物基因是可能的



1.4 直言命题(所有有些)
- 直言命题(定言命题):即性质命题,是断定事物性质的简单命题。
由于在性质命题中,对 对象 具有或不具有某种性质的断定是直接的、无条件的,因而,逻辑史上把这种命题称为直言命题,以 别于假言命题(对对象的某种断定是有条件的)和选言命题(对对象的某种断定是有选择的)
eg1:所有事物都是运动的
eg2:有些四边形是矩形
eg3:小李是申论讲师



小结:


总结
- 翻译规则



相关文章:

【判断推理】逻辑基础
1.1 命题 用语言、符号或者式子表达的,可以判断真假的陈述句称为命题,一般写为 若p,则q 真命题:判断为真的语句假命题:判断为假的语句 eg1:小张是中国人(若是小张,则是中国人&#…...

AcWing 655:天数转换 ← 整除、求余
【题目来源】https://www.acwing.com/problem/content/657/【题目描述】 读取对应于一个人的年龄(以天为单位)的整数值,并转化为年,月和日表示方式输出,年、月、日分别对应 ano(s), mes(es), dia(s)。 注意:…...

【解决办法】git clone报错unable to access ‘xxx‘: SSL certificate problem:
使用git clone 时报错unable to access xxx: SSL certificate problem: 这个报错通常是由于SSL证书问题引起的。通常可以按照以下步骤进行排查: 检查网络连接:确保你的网络连接正常,可以访问互联网。尝试使用其他网站或工具测试网络连接是否正…...

算法笔记(十三)——BFS 解决最短路问题
文章目录 迷宫中离入口最近的出口最小基因变化单词接龙为高尔夫比赛砍树 BFS 解决最短路问题 BFS(广度优先搜索) 是解决最短路径问题的一种常见算法。在这种情况下,我们通常使用BFS来查找从一个起始点到目标点的最短路径。 迷宫中离入口最近的出口 题目:…...

Android 简单实现联系人列表+字母索引联动效果
效果如上图。 Main Ideas 左右两个列表左列表展示人员数据,含有姓氏首字母的 header item右列表是一个全由姓氏首字母组成的索引列表,点击某个item,展示一个气泡组件(它会自动延时关闭), 左列表滚动并显示与点击的索引列表item …...

自动驾驶-问题笔记-待解决
参考线的平滑方法 参考线平滑算法主要有三种: 离散点平滑;螺旋曲线平滑;多项式平滑; 参考链接:参考线平滑 对于平滑方法,一直不太理解平滑、拟合以及滤波三者的作用与区别; 规划的起点&#x…...

在掌控板中加载人教版信息科技教学指南中的educore库
掌控板中加载educore库 人教信息科技数字资源平台(https://ebook.mypep.cn/free)中的《信息科技教学指南硬件编程代码说明》文件中提到“本程序说明主要供教学参考。需要可编程主控板须支持运行MicroPython 脚本程序。希望有更多的主控板在固件中支持ed…...

关于CSS Grid布局
关于CSS Grid布局 实际效果参考 参考代码 <template><view class"baseInfo"><up-image class"cover" height"160rpx" width"120rpx" :src"bookInfo.cover"><template #error><view style"…...

初始爬虫12(反爬与反反爬)
学到这里,已经可以开始实战项目了,多去爬虫,了解熟悉反爬,然后自己总结出一套方法怎么做。 1.服务器反爬的原因 服务器反爬的原因 总结: 1.爬虫占总PV较高,浪费资源 2.资源被批量抓走,丧失竞争力…...

成像基础 -- 最大对焦清晰的物距计算
最大对焦清晰的物距计算 1. 基本概念 最大对焦清晰的物距通常与景深(Depth of Field, DOF)相关,尤其是无穷远处的物体可以被清晰对焦到的距离,称为超焦距(Hyperfocal Distance)。通过计算超焦距ÿ…...

win10服务器启动且未登录时自动启动程序
场景:公司服务器安装了几个程序,当服务器断电重启之后希望程序能自动打开,而不需要手动登录服务器打开。 因为软件是自己开发的所以安全方面这里没有考虑。 1.打开服务器管理器,点击工具,选择任务计划程序 2.在任务计…...

算法专题四: 前缀和
目录 1. 前缀和2. 二维前缀和3. 寻找数组的中心下标4. 除自身以外数组的乘积5. 和为k的子数组6. 和可被K整除的子数组7. 连续数组8. 矩阵区域和 博客主页:酷酷学!!! 感谢关注~ 1. 前缀和 算法思路: 根据题意, 创建一个前缀和数组, dp[i] dp[i -1] arr[i], 再使用前缀和数组,…...

【Linux】基础IO(文件描述符、缓冲区、重定向)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12625432.html 目录 前言 C文件IO相关操作 系统文件I/O open open函数返回值 文件描述符fd re…...

一篇文章快速学会docker容器技术
目录 一、Docker简介及部署方法 1.1Docker简介 1.1.1什么是docker 1.1.2 docker在企业中的应用场景 1.1.3 docker与虚拟化的对比 1.1.4 docker的优势 二 、部署docker 2.1 容器工作方法 2.2 部署第一个容器 2.2.1 配置软件仓库 2.2.2 安装docker-ce并启动服务 2.2.…...
【MySQL】使用 JDBC 连接数据库
文章目录 前言1. 认识 JDBC1.1 概念1.2 好处 2. 使用 JDBC2.1 安装数据驱动包2.2 把 jar 包导入到项目中2.3 代码编写2.4 测试结果 3. 代码优化4. 源码展示结语 前言 在 MySQL 系列中,我们介绍了很多内容,包括但不限于建库建表,增删查改等等…...

数据结构与算法笔记:概念与leetcode练习题
1、数组Array 时间复杂度 数组访问:O(1) 数组搜索:O(N) 数组插入:O(N) 数组删除:O(N) 特点 适合读,不适合写 数组常用操作 # 1、创建数组 a [] # 2、尾部添加元素 a.append(1) a.append(2) a.append(3) # 3、…...
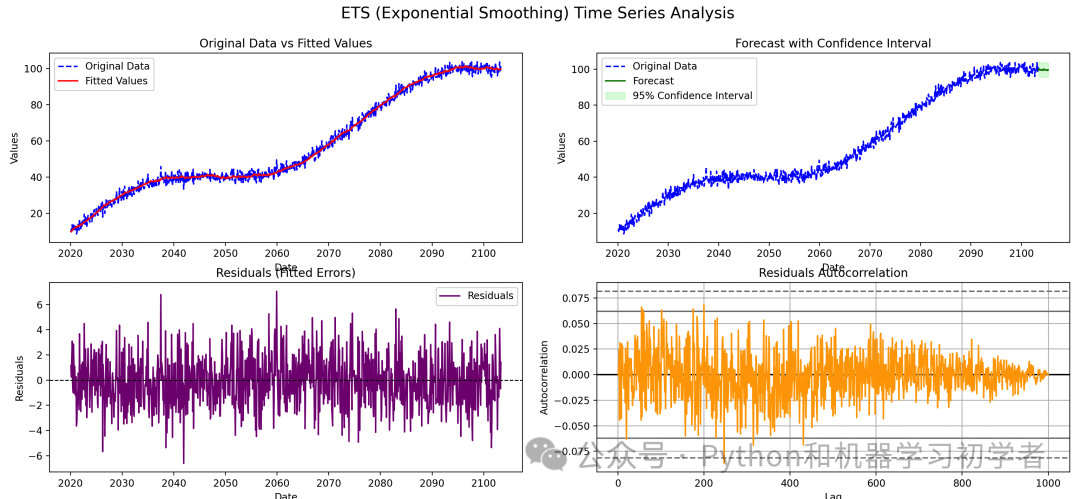
十大时间序列预测模型
目录 1. 自回归模型 原理 核心公式 推导过程: 完整案例 2. 移动平均模型 原理 核心公式 推导过程: 完整案例 3. 自回归移动平均模型 原理 核心公式 推导过程: 完整案例 4. 自回归积分移动平均模型 原理 核心公式 推导过程 完整案例 5. 季节性自回归积分…...

G2O 通过工厂函数类 OptimizationAlgorithmFactory 来生成固定搭配的优化算法
OptimizationAlgorithmFactory 类位于 optimization_algorithm_factory.h //***g2o源码 g2o/g2o/core/optimization_algorithm_factory.h ***// /*** \brief create solvers based on their short name** Factory to allocate solvers based on their short name.* The Factor…...

手机USB连接不显示内部设备,设备管理器显示“MTP”感叹号,解决方案
进入小米驱动下载界面,等小米驱动下载完成后,解压此驱动文件压缩包。 5、小米USB驱动安装方法:右击“计算机”,从弹出的右键菜单中选择“管理”项进入。 6、在打开的“计算机管理”界面中,展开“设备管理器”项&…...

SpringBootWeb快速入门!详解如何创建一个简单的SpringBoot项目?
在现代Web开发中,SpringBoot以其简化的配置和快速的开发效率而受到广大开发者的青睐。本篇文章将带领你从零开始,搭建一个基于SpringBoot的简单Web应用~ 一、前提准备 想要创建一个SpringBoot项目,需要做如下准备: idea集成开发…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
