Web3与人工智能的交叉应用探索
随着数字技术的发展,Web3与人工智能(AI)之间的结合正逐渐成为一个重要的研究领域。Web3技术旨在实现更加去中心化和透明的互联网,而人工智能则在数据分析、自动化决策和增强人类能力方面展示了巨大的潜力。

1. 去中心化数据管理与AI的数据需求
AI依赖大量数据来进行有效的学习和预测,而Web3为数据的去中心化管理提供了强大的支持。传统的集中式数据存储方式存在数据泄露的风险,而Web3则通过区块链和分布式存储技术实现了数据的去中心化,保障了用户的数据隐私。通过使用去中心化存储网络(如IPFS、Filecoin),AI模型可以从安全且分布式的数据源中提取数据,不仅增强了数据的安全性,还赋予了用户对数据的更多控制权。
在这种环境下,AI可以在去中心化的数据池中自由获取信息,同时确保数据的所有权归用户自己。这为AI算法的训练和应用提供了新的可能性,也使得数据隐私和安全性得到了更好的保障。
2. 自主化智能合约的实现
智能合约是Web3的重要组成部分,而AI的加入则为智能合约注入了更强的自主性。智能合约通常按照预设的规则自动执行交易,但其逻辑相对固定,无法处理复杂的外部情况。通过引入AI,智能合约可以在执行过程中进行实时学习,并对外部数据做出灵活的响应。例如,一个AI驱动的智能合约可以通过分析市场趋势来自主调整交易策略,为用户带来更高的经济效益。
这种自主化智能合约的应用场景包括去中心化金融(DeFi)、供应链管理和自动化保险理赔等。AI在其中的角色是增强智能合约的灵活性,使其能够处理复杂的环境变量,从而更好地满足用户的需求。
3.增强的自主决策能力
传统智能合约按照硬编码规则执行任务,但在处理复杂情况时,缺乏动态决策能力。引入 AI 后,智能合约可以实时分析外部数据,根据不同的情境调整执行方案。例如,一个涉及金融资产的合约可以通过 AI 分析市场走势,并根据实时价格变化自动调整投资策略。结合 ClonBrowser ,用户可以匿名参与多个 AI 驱动的智能合约,确保他们的数据和隐私在整个决策过程中不被泄露。

4. 去中心化自治组织(DAO)的智能管理
去中心化自治组织(DAO)是Web3中的一种新型治理结构,其运作依赖于集体决策和智能合约。AI可以在DAO中发挥重要作用,通过分析成员的行为和提案的历史数据,为组织决策提供数据支持。例如,一个带有AI算法的DAO可以对提案进行评估,预测其成功率,或者为特定类型的决策推荐更合适的投票机制。这不仅提高了DAO的决策效率,还可以帮助组织更好地适应不断变化的外部环境。
此外,AI还可以被用来管理DAO中的人力资源。通过分析成员的技能和贡献情况,AI可以建议最适合的任务分配,确保资源的合理利用。这样的自动化管理不仅降低了DAO的运营成本,还能提高其整体效率。
5. 个人数据主权与AI模型训练
在Web3环境中,用户拥有数据的完全控制权,这与AI模型训练的需求形成了良好的互补。通过Web3的去中心化身份(DID)系统,用户可以安全地存储、分享和控制自己的数据。AI可以基于这些数据进行分布式学习,确保用户隐私的同时,完成所需的模型训练。
例如,通过采用“联邦学习”技术,AI模型可以在各个用户设备上独立训练,而无需将数据集中在一个服务器中。这种方式下,用户的数据不离开设备,AI算法可以基于分布式的数据集合进行更新。这种结合不仅保护了用户隐私,还提供了高质量的数据源,从而提升了模型的性能。

结语
Web3与人工智能的结合为未来的科技发展带来了无限可能。这种交叉应用不仅在技术层面有着广泛的应用前景,更代表了一种新的互联网理念,即将去中心化和智能化带入我们的日常生活。通过积极探索和推进这些技术的结合,我们将能够构建出一个更加开放、透明和高效的未来互联网生态。
相关文章:

Web3与人工智能的交叉应用探索
随着数字技术的发展,Web3与人工智能(AI)之间的结合正逐渐成为一个重要的研究领域。Web3技术旨在实现更加去中心化和透明的互联网,而人工智能则在数据分析、自动化决策和增强人类能力方面展示了巨大的潜力。 1. 去中心化数据管理与…...

【springboot9736】基于springboot+vue的逍遥大药房管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 项目描述 伴随着全球信息化发展,行行业业都与计算机技…...

四.网络层(上)
目录 4.1网络层功能概述 4.2 SDN基本概念 4.3 路由算法与路由协议 4.3.1什么是路由协议? 4.3.2什么是路由算法? 4.3.3路由算法分类 (1)静态路由算法 (2)动态路由算法 ①全局性 OSPF协议与链路状态算法 ②分散性 RIP协议与距离向量算法 4.3.…...

Leecode热题100-56.合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:intervals [[1,3…...

安全帽未佩戴预警系统 劳保防护用品穿戴监测系统 YOLO
在建筑、矿山、电力等高危行业中,工人面临着各种潜在的危险,如高空坠物、物体打击等。安全帽能够有效地分散和吸收冲击力,大大降低头部受伤的严重程度。一旦工人未正确佩戴安全帽,在遭遇危险时,头部将直接暴露在危险之…...

【python机器学习】线性回归 拟合 欠拟合与过拟合 以及波士顿房价预估案例
文章目录 线性回归之波士顿房价预测案例 欠拟合与过拟合线性回归API 介绍:波士顿房价预测数据属性:机器学习代码实现 拟合 过拟合 欠拟合 模拟 及处理方法(正则化处理)导包定义函数表示欠拟合定义函数表示拟合定义函数表示过拟合 正则化处理过拟合L1正则化L2正则化 线性回归之波…...

IT招聘乱象的全面分析
近年来,IT行业的招聘要求似乎越来越苛刻,甚至有些不切实际。许多企业在招聘时,不仅要求前端工程师具备UI设计能力,还希望后端工程师精通K8S服务器运维,更有甚至希望研发经理掌握所有前后端框架和最新开发技术。这种招聘…...

一入递归深似海,算法之美无止境
最近在刷leetcode hot100,在写二叉树中最大路径和的时候,看到了一个佬对递归的理解,深受启发,感觉自己对于递归的题又行了!!! 这里给大家分享一下(建立大家先去尝试一下这道题再来看 124. 二叉树中的最大路径和 二叉树中的 路径 被定义为一条节点序列,序列中每…...

进程的状态的理解(概念+Linux)
文章目录 进程的状态并行和并发物理和逻辑 时间片进程具有独立性等待的本质运行阻塞标记挂起等待 Linux下的进程状态(一)运行状态(R - running)(二)睡眠状态(S - sleeping)ÿ…...

Apache Linkis + OceanBase:如何提升数据分析效率
计算中间件 Apache Linkis 构建了一个计算中间件层,以实现上层应用程序和底层数据引擎之间的连接、治理和编排。目前,已经支持通过数据源的功能,实现用户通过Linkis 对接并使用 OceanBase数据库。 本文详细阐述了在 Apache Linkis v1.3.2中&a…...
Day01-postgresql数据库基础入门培训
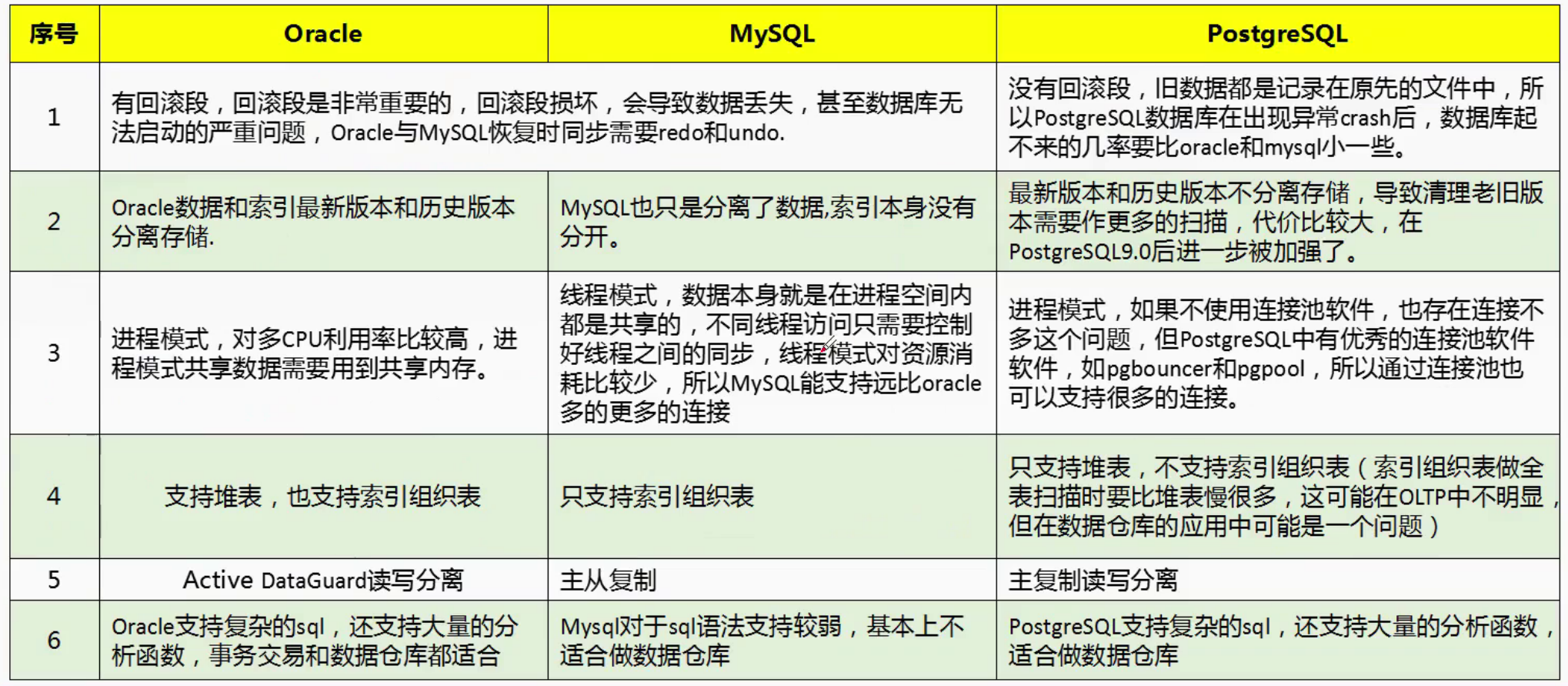
Day01-postgresql数据库基础入门培训 1、PostgresQL数据库简介2、PostgreSQL行业生态应用3、PostgreSQL版本发展与特性4、PostgreSQL体系结构介绍5、PostgreSQL与MySQL的区别6、PostgreSQL与Oracle、MySQL的对比 1、PostgresQL数据库简介 PostgreSQL【简称:PG】是加…...

打卡第四天 P1081 [NOIP2012 提高组] 开车旅行
今天是我打卡第四天,做个省选/NOI−题吧(#^.^#) 原题链接:[NOIP2012 提高组] 开车旅行 - 洛谷 题目描述 输入格式 输出格式 输入输出样例 输入 #1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 输出 #1 1 1 1 2 0 0 0 0 0 输入 #2 10 4 5 6 1 …...

Jenkins Pipline流水线
提到 CI 工具,首先想到的就是“CI 界”的大佬--]enkjns,虽然在云原生爆发的年代,蹦出来了很多云原生的 CI 工具,但是都不足以撼动 Jenkins 的地位。在企业中对于持续集成、持续部署的需求非常多,并且也会经常有-些比较复杂的需求,此时新生的 CI 工具不足以支撑这些很…...

鸿蒙harmonyos next flutter混合开发之开发FFI plugin
创建FFI plugin summation,默认创建的FFI plugin是求两个数的和 flutter create --templateplugin_ffi summation --platformsandroid,ios,ohos 创建my_application flutter create --org com.example my_application 在my_application项目中文件pubspec.yaml引…...

oracle数据库安装和配置
Oracle数据库安装 一、安装前的准备 系统要求: 硬件:内存至少1GB(推荐2GB以上),硬盘至少10GB的可用空间,CPU至少2核心。 操作系统:支持Oracle版本的Windows(如Windows 10或更高版本…...

猫玖破密啦
题目: 终究还是猫哥:3d5a3a0cfff7fb2e29194c0b7a89f284ff19a8 玖离:收到消息Oh,what_is_the_flag 玖离:7468655f666c61675f69735f666c13556d2cf2faec1e2d0f330b7dcceea1c62cb2 终究还是猫哥:收到消息************************************ 已…...

SpringBoot框架:服装生产管理的现代化工具
摘 要 本协力服装厂服装生产管理系统设计目标是实现协力服装厂服装生产的信息化管理,提高管理效率,使得协力服装厂服装生产管理作规范化、科学化、高效化。 本文重点阐述了协力服装厂服装生产管理系统的开发过程,以实际运用为开发背景&#…...

Android Preference的使用以及解析
简单使用 values.arrays.xml <?xml version"1.0" encoding"utf-8"?> <resources><string-array name"list_entries"><item>Option 1</item><item>Option 2</item><item>Option 3</item&…...

HCIP——GRE和MGRE
目录 VPN GRE GRE环境的搭建 GRE的报文结构 GRE封装和解封装报文的过程 GRE配置编辑 R1 R2 GRE实验编辑 MGRE 原理 MGRE的配置 R1 R2 R3 R4 查看映射表 抓包 MGRE环境下的RIP网络 综合练习编辑 VPN 说到GRE,我们先来说个大…...

微信小程序——音乐播放器
一、界面设计 播放页面: 显示当前播放歌曲的封面图片、歌曲名称、歌手名称。有播放 / 暂停按钮、上一首、下一首按钮。进度条显示播放进度,可以拖动进度条调整播放位置。音量调节滑块。 歌曲列表页面: 展示歌曲列表,包括歌曲名称、…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
