Java 归并排序
归并排序(Merge Sort)是一种基于分治法的排序算法。它将一个大数组分成两个较小的子数组,分别对每个子数组进行排序,然后再将这两个已排序的子数组合并成一个完整的已排序数组。归并排序的时间复杂度为 O(n log n),其中 n 是数组的大小。
以下是一个 Java 实现归并排序的示例:
public class MergeSort { // 主函数,用于测试归并排序 public static void main(String[] args) { int[] array = {38, 27, 43, 3, 9, 82, 10}; System.out.println("给定数组:"); printArray(array); mergeSort(array, 0, array.length - 1); System.out.println("\n排序后的数组:"); printArray(array); } // 归并排序函数 public static void mergeSort(int[] array, int left, int right) { if (left < right) { // 找到中间点 int middle = (left + right) / 2; // 对左半部分进行排序 mergeSort(array, left, middle); // 对右半部分进行排序 mergeSort(array, middle + 1, right); // 合并已排序的左右两部分 merge(array, left, middle, right); } } // 合并函数 public static void merge(int[] array, int left, int middle, int right) { // 找到两个子数组的大小 int n1 = middle - left + 1; int n2 = right - middle; // 创建临时数组 int[] leftArray = new int[n1]; int[] rightArray = new int[n2]; // 拷贝数据到临时数组 for (int i = 0; i < n1; ++i) leftArray[i] = array[left + i]; for (int j = 0; j < n2; ++j) rightArray[j] = array[middle + 1 + j]; // 合并临时数组到原数组 // 初始索引分别为两个子数组的起始位置 int i = 0, j = 0; // 初始索引为合并子数组的起始位置 int k = left; while (i < n1 && j < n2) { if (leftArray[i] <= rightArray[j]) { array[k] = leftArray[i]; i++; } else { array[k] = rightArray[j]; j++; } k++; } // 拷贝左子数组剩余的元素(如果有) while (i < n1) { array[k] = leftArray[i]; i++; k++; } // 拷贝右子数组剩余的元素(如果有) while (j < n2) { array[k] = rightArray[j]; j++; k++; } } // 打印数组函数 public static void printArray(int[] array) { int n = array.length; for (int i = 0; i < n; ++i) System.out.print(array[i] + " "); System.out.println(); }
}代码解释:
mergeSort方法:- 递归地将数组分成左右两部分,直到每部分只有一个元素或为空。
- 递归调用
mergeSort方法对左右两部分进行排序。 - 调用
merge方法将已排序的左右两部分合并成一个完整的已排序数组。
merge方法:- 创建两个临时数组
leftArray和rightArray分别存储左右两部分。 - 将左右两部分分别拷贝到临时数组中。
- 使用两个指针
i和j分别遍历临时数组leftArray和rightArray。 - 使用一个指针
k遍历原数组,根据临时数组中的元素大小,将较小的元素依次拷贝回原数组。 - 如果某一临时数组的元素已经拷贝完,则将另一临时数组的剩余元素拷贝回原数组。
- 创建两个临时数组
printArray方法:- 用于打印数组中的元素。
运行结果:
程序运行后,会先打印给定的数组,然后打印排序后的数组。
归并排序是一个稳定的排序算法,适用于大多数需要排序的场景。它的空间复杂度为 O(n),因为需要额外的临时数组来存储子数组的元素。
相关文章:

Java 归并排序
归并排序(Merge Sort)是一种基于分治法的排序算法。它将一个大数组分成两个较小的子数组,分别对每个子数组进行排序,然后再将这两个已排序的子数组合并成一个完整的已排序数组。归并排序的时间复杂度为 O(n log n),其中…...

20241008深度学习动手篇
文章目录 1.如何写一个神经网络进行训练?1.1创建一个子类,搭建你需要的神经网络结构1.2 加载数据集1.3 自定义一些指标评估函数1.4训练1.5 结果展示 2.参考文献 1.如何写一个神经网络进行训练? 1.1创建一个子类,搭建你需要的神经网络结构 # File: 241008LeNet.py # Author:…...

对序列化反序列化在项目中的使用优化
文章目录 序列化是什么?常见的序列化协议使用序列化反序列化序列化List反序列化List 查看源码,分析不足进行改善 序列化是什么? 如果我们需要持久化 Java 对象比如将 Java 对象保存在文件中,或者在网络传输 Java 对象,…...

查看 git log的过程中看到 :说明日志输出可能超出屏幕大小,系统进入了分页模式
在命令行提示符中,通常 : 表示系统等待进一步的输入。如果你在查看 git log 的过程中看到 :,说明日志输出可能超出屏幕大小,系统进入了分页模式,默认使用 less 命令查看内容。 此时你可以: 按 q 退出日志查看。按 En…...

Linux--信号量详解
目录 一、信号量 1、信号量相关函数 2、多线程环形队列生产消费模型 3、实现代码 信号量是将整体的资源分割成多份使用 信号量本质是对资源的预定机制 一、信号量 1、信号量相关函数 创建信号量: sem_init: int sem_init(sem_t *sem, int pshared, unsigned int value); …...

【重学 MySQL】五十一、更新和删除数据
【重学 MySQL】五十一、更新和删除数据 更新数据删除数据注意事项 在MySQL中,更新和删除数据是数据库管理的基本操作。 更新数据 为了更新(修改)表中的数据,可使用UPDATE语句。UPDATE语句的基本语法如下: UPDATE ta…...

Web3与人工智能的交叉应用探索
随着数字技术的发展,Web3与人工智能(AI)之间的结合正逐渐成为一个重要的研究领域。Web3技术旨在实现更加去中心化和透明的互联网,而人工智能则在数据分析、自动化决策和增强人类能力方面展示了巨大的潜力。 1. 去中心化数据管理与…...

【springboot9736】基于springboot+vue的逍遥大药房管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 项目描述 伴随着全球信息化发展,行行业业都与计算机技…...

四.网络层(上)
目录 4.1网络层功能概述 4.2 SDN基本概念 4.3 路由算法与路由协议 4.3.1什么是路由协议? 4.3.2什么是路由算法? 4.3.3路由算法分类 (1)静态路由算法 (2)动态路由算法 ①全局性 OSPF协议与链路状态算法 ②分散性 RIP协议与距离向量算法 4.3.…...

Leecode热题100-56.合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1: 输入:intervals [[1,3…...

安全帽未佩戴预警系统 劳保防护用品穿戴监测系统 YOLO
在建筑、矿山、电力等高危行业中,工人面临着各种潜在的危险,如高空坠物、物体打击等。安全帽能够有效地分散和吸收冲击力,大大降低头部受伤的严重程度。一旦工人未正确佩戴安全帽,在遭遇危险时,头部将直接暴露在危险之…...

【python机器学习】线性回归 拟合 欠拟合与过拟合 以及波士顿房价预估案例
文章目录 线性回归之波士顿房价预测案例 欠拟合与过拟合线性回归API 介绍:波士顿房价预测数据属性:机器学习代码实现 拟合 过拟合 欠拟合 模拟 及处理方法(正则化处理)导包定义函数表示欠拟合定义函数表示拟合定义函数表示过拟合 正则化处理过拟合L1正则化L2正则化 线性回归之波…...

IT招聘乱象的全面分析
近年来,IT行业的招聘要求似乎越来越苛刻,甚至有些不切实际。许多企业在招聘时,不仅要求前端工程师具备UI设计能力,还希望后端工程师精通K8S服务器运维,更有甚至希望研发经理掌握所有前后端框架和最新开发技术。这种招聘…...

一入递归深似海,算法之美无止境
最近在刷leetcode hot100,在写二叉树中最大路径和的时候,看到了一个佬对递归的理解,深受启发,感觉自己对于递归的题又行了!!! 这里给大家分享一下(建立大家先去尝试一下这道题再来看 124. 二叉树中的最大路径和 二叉树中的 路径 被定义为一条节点序列,序列中每…...

进程的状态的理解(概念+Linux)
文章目录 进程的状态并行和并发物理和逻辑 时间片进程具有独立性等待的本质运行阻塞标记挂起等待 Linux下的进程状态(一)运行状态(R - running)(二)睡眠状态(S - sleeping)ÿ…...

Apache Linkis + OceanBase:如何提升数据分析效率
计算中间件 Apache Linkis 构建了一个计算中间件层,以实现上层应用程序和底层数据引擎之间的连接、治理和编排。目前,已经支持通过数据源的功能,实现用户通过Linkis 对接并使用 OceanBase数据库。 本文详细阐述了在 Apache Linkis v1.3.2中&a…...
Day01-postgresql数据库基础入门培训
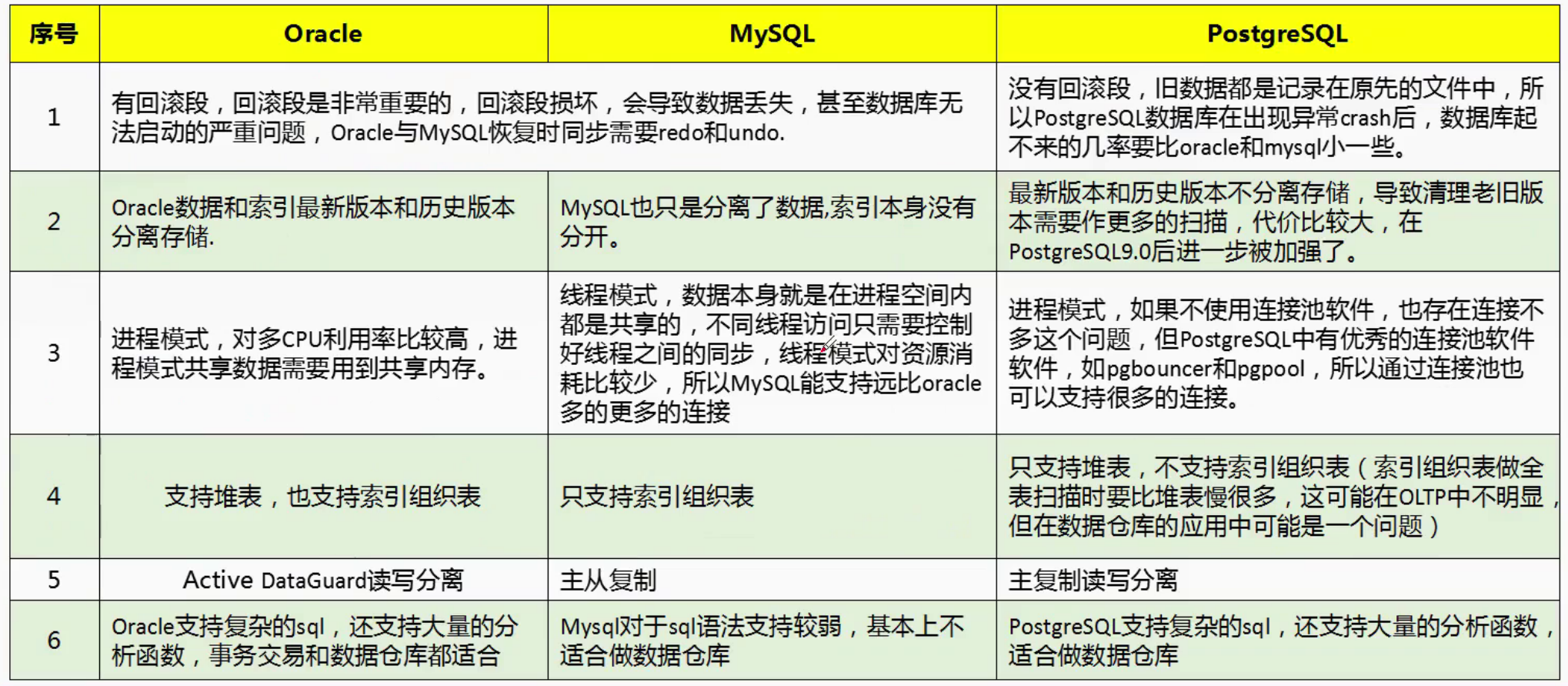
Day01-postgresql数据库基础入门培训 1、PostgresQL数据库简介2、PostgreSQL行业生态应用3、PostgreSQL版本发展与特性4、PostgreSQL体系结构介绍5、PostgreSQL与MySQL的区别6、PostgreSQL与Oracle、MySQL的对比 1、PostgresQL数据库简介 PostgreSQL【简称:PG】是加…...

打卡第四天 P1081 [NOIP2012 提高组] 开车旅行
今天是我打卡第四天,做个省选/NOI−题吧(#^.^#) 原题链接:[NOIP2012 提高组] 开车旅行 - 洛谷 题目描述 输入格式 输出格式 输入输出样例 输入 #1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 输出 #1 1 1 1 2 0 0 0 0 0 输入 #2 10 4 5 6 1 …...

Jenkins Pipline流水线
提到 CI 工具,首先想到的就是“CI 界”的大佬--]enkjns,虽然在云原生爆发的年代,蹦出来了很多云原生的 CI 工具,但是都不足以撼动 Jenkins 的地位。在企业中对于持续集成、持续部署的需求非常多,并且也会经常有-些比较复杂的需求,此时新生的 CI 工具不足以支撑这些很…...

鸿蒙harmonyos next flutter混合开发之开发FFI plugin
创建FFI plugin summation,默认创建的FFI plugin是求两个数的和 flutter create --templateplugin_ffi summation --platformsandroid,ios,ohos 创建my_application flutter create --org com.example my_application 在my_application项目中文件pubspec.yaml引…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
