第二十二天|回溯算法| 理论基础,77. 组合(剪枝),216. 组合总和III,17. 电话号码的字母组合
目录
回溯算法理论基础
1.题目分类
2.理论基础
3.回溯法模板
补充一个JAVA基础知识
什么时候用ArrayList什么时候用LinkedList
77. 组合
未剪枝优化
剪枝优化
216. 组合总和III
17. 电话号码的字母组合
回溯法的一个重点理解:细细理解这句话!
回溯法抽象为树形结构后,其遍历过程就是:for循环横向遍历,递归纵向遍历,回溯不断调整结果集。
回溯算法理论基础
1.题目分类

2.理论基础
- 什么是回溯算法
回溯和递归是相辅相成的。
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。
- 回溯法的效率
回溯法其实就是暴力查找,并不是什么高效的算法。
因为回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
- 回溯法可以解决几类问题
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
3.回溯法模板
回溯法解决的问题都可以抽象为树形结构(N叉树)。
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}回溯三部曲:
- 回溯函数模板返回值以及参数
回溯算法中函数返回值一般为void。先写逻辑,然后需要什么参数,就填什么参数。
- 回溯函数终止条件
一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
- 回溯搜索的遍历过程
for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了。
补充一个JAVA基础知识
什么时候用ArrayList什么时候用LinkedList
1. 存储结构与基本概念:
-
ArrayList:
- 底层是基于数组的数据结构。
- 元素是连续存储的,这意味着可以通过索引快速访问元素。
- 如果数组容量不足时,
ArrayList会创建一个更大的数组并将原数组的元素复制到新数组中。
-
LinkedList:
- 底层是基于双向链表的数据结构。
- 每个节点存储元素值及前一个和后一个节点的引用。
- 元素在内存中不必是连续的,增删节点时不需要像
ArrayList那样复制数组。
2. 选择依据:
-
使用
ArrayList的场景:- 需要频繁访问元素:由于
ArrayList基于数组结构,可以通过索引在O(1)时间内访问任意元素,因此如果你的主要操作是访问而不是插入和删除,ArrayList会更适合。 - 元素数量较多,但插入和删除操作较少:
ArrayList在添加元素时,只要不超出容量,添加时间是O(1),但当数组需要扩容时,时间复杂度会变为O(n)。 - 遍历操作较多:
ArrayList因为底层是连续内存存储,遍历时缓存命中率较高,因此在遍历时性能会比LinkedList好。
- 需要频繁访问元素:由于
-
使用
LinkedList的场景:- 需要频繁的插入和删除操作:
LinkedList在头部或中间插入/删除元素时,不需要移动其他元素,只需要调整指针即可,效率更高。如果你的操作集中在头部或尾部,LinkedList会表现更好。 - 需要在列表的任意位置频繁插入/删除:在这种情况下,
LinkedList可以通过调整节点的指向来高效完成操作,而ArrayList则需要移动元素来维护数组的连续性。 - 存储的元素数量不大且不需要频繁访问:
LinkedList的随机访问时间是O(n),因此如果需要频繁通过索引访问元素,LinkedList性能较差。
- 需要频繁的插入和删除操作:
3. 总结选择:
- 如果主要是读操作(访问元素):选择
ArrayList。 - 如果主要是写操作(插入、删除),并且特别是在头部或中间:选择
LinkedList。 - 如果数据规模大,并且需要高效的遍历:
ArrayList更好。 - 如果数据规模小,并且操作模式比较多变:
LinkedList的灵活性更好。
4. 示例应用场景:
-
使用
ArrayList:List<String> arrayList = new ArrayList<>(); arrayList.add("a"); // O(1) - 添加元素 arrayList.get(0); // O(1) - 通过索引访问 -
使用
LinkedList:LinkedList<String> linkedList = new LinkedList<>(); linkedList.addFirst("a"); // O(1) - 在头部插入 linkedList.removeFirst(); // O(1) - 从头部删除
77. 组合
本题是回溯法的经典题目。
把组合问题抽象为如下树形结构:
图中每次搜索到了叶子节点,我们就找到了一个结果。
相当于只需要把达到叶子节点的结果收集起来,就可以求得 n个数中k个数的组合集合。

未剪枝优化
回溯法三部曲
- 递归函数的返回值以及参数
vector<vector<int>> result; // 存放符合条件结果的集合
vector<int> path; // 用来存放符合条件单一结果
void backtracking(int n, int k, int startIndex)函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。startIndex 就是防止出现重复的组合。需要startIndex来记录下一层递归,搜索的起始位置。
- 回溯函数终止条件
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。
此时用result二维数组,把path保存起来,并终止本层递归。
if (path.size() == k) {result.push_back(path);return;
}- 单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。
backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。

- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n)
整体代码如下:
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {// 未剪枝优化backtracking(n, k, 1);return result;}// 递归的每一层在执行完所有可能的路径(所有从startIndex到n的i)之后,会自然退出当前循环,并结束当前的backtracking调用。public void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n; i++) {path.add(i);backtracking(n, k, i + 1);// 在递归调用返回之后,path.removeLast()会将最后添加的元素移除,以准备下一轮循环中添加不同的元素。path.removeLast();}}}剪枝优化
剪枝的目标是减少不必要的递归调用,避免继续探索那些不可能满足条件的路径,从而提高效率。
来举一个例子,n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
这么说有点抽象,如图所示:

可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
优化过程如下:
-
已经选择的元素个数:path.size();
-
还需要的元素个数为: k - path.size();
-
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置为什么是 n - (k - path.size()) + 1:(重点理解一下)
-
n - (k - path.size()) + 1的含义是:k - path.size():当前还需要选择的元素数量。n - (k - path.size()):表示当前可选择元素的最大起始位置,即从这个位置开始,剩余的元素刚好足够填充到k个。+1是为了让i的范围包含这个起始位置。
-
例如,如果
n = 5,k = 3,并且当前path.size() = 1,也就是已经选择了一个元素,还需要选择2个元素。- 此时,
k - path.size() = 3 - 1 = 2。 n - (k - path.size()) = 5 - 2 = 3。- 所以,
i的最大值是3 + 1 = 4。 - 换句话说,从
i = 4开始时,只有4和5两个元素可选,这正好可以凑齐3个元素的组合。
- 此时,
剪枝示例进一步理解:
假设n = 5,k = 3,我们在不同的递归层次下看i的取值范围:
-
当
path.size() = 0(还没选任何元素)时:- 需要选
k = 3个元素。 - 可选择范围是:
i <= 5 - (3 - 0) + 1 = 3,所以i可以从1到3。 - 选择
1时,递归进入下一层。
- 需要选
-
当
path.size() = 1(已选择1)时:- 需要再选
2个元素。 - 可选择范围是:
i <= 5 - (3 - 1) + 1 = 4,所以i可以从2到4。
- 需要再选
-
当
path.size() = 2(已选择1, 2)时:- 需要再选
1个元素。 - 可选择范围是:
i <= 5 - (3 - 2) + 1 = 5,所以i可以从3到5。
- 需要再选
-
以此类推,当
path.size() == k时,就停止递归,将结果存入result。
优化后整体代码如下:
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {combineHelper(n, k, 1);return result;}/*** 每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex* @param startIndex 用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。*/private void combineHelper(int n, int k, int startIndex){//终止条件if (path.size() == k){result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){path.add(i);combineHelper(n, k, i + 1);path.removeLast();}}
}216. 组合总和III
本题就是在77基础上多了一个求和的限制罢了,简单。
注意:处理过程 和 回溯过程是一一对应的,处理有加,回溯就要有减
这里我自己写的时候漏了一个sum -= i的回溯
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();int sum = 0;public List<List<Integer>> combinationSum3(int k, int n) {backTrackingSum(k, n, 1);return result;}private void backTrackingSum(int k, int n, int startIndex) {if (sum > n) return; // 剪枝if (path.size() == k) {if (sum == n) {result.add(new ArrayList<>(path));}return;}// 剪枝 9 - (k - path.size()) + 1for (int i = startIndex; i <= 10 - (k - path.size()); i++) {path.add(i);sum += i;backTrackingSum(k, n, i + 1);sum -= i; // 回溯path.removeLast(); //回溯}}}// 上面剪枝 i <= 9 - (k - path.size()) + 1; 如果还是不清楚
// 也可以改为 if (path.size() > k) return; 执行效率上是一样的class Solution {LinkedList<Integer> path = new LinkedList<>();List<List<Integer>> ans = new ArrayList<>();public List<List<Integer>> combinationSum3(int k, int n) {build(k, n, 1, 0);return ans;}private void build(int k, int n, int startIndex, int sum) {if (sum > n) return;if (path.size() > k) return;if (sum == n && path.size() == k) {ans.add(new ArrayList<>(path));return;}for(int i = startIndex; i <= 9; i++) {path.add(i);sum += i;build(k, n, i + 1, sum);sum -= i;path.removeLast();}}
}17. 电话号码的字母组合
本题需要多理解一下递归逻辑,看着代码
本题就是要解决如下三个问题:
- 数字和字母如何映射
- 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
- 输入1 * #按键等等异常情况
数字和字母如何映射
可以使用map或者定义一个二维数组,例如:string letterMap[10],来做映射。
回溯法来解决n个for循环的问题

回溯三部曲:
- 确定回溯函数参数
首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来。
参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
- 确定终止条件
终止条件就是如果index 等于 输入的数字个数(digits.size)了,就收集结果,结束本层递归。
- 确定单层遍历逻辑
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {s.push_back(letters[i]); // 处理backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了s.pop_back(); // 回溯
}整体代码如下。需要多理解一下:
class Solution {//设置全局列表存储最后的结果List<String> list = new ArrayList<>();public List<String> letterCombinations(String digits) {if (digits == null || digits.length() == 0) {return list;}//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};//迭代处理backTraciking(digits, numString, 0);return list;}//每次迭代获取一个字符串,所以会涉及大量的字符串拼接,所以这里选择更为高效的 StringBuilderStringBuilder temp = new StringBuilder();//比如digits如果为"23",num 为0,则str表示2对应的 abcpublic void backTraciking(String digits, String[] numString, int num) {//遍历全部一次记录一次得到的字符串if (num == digits.length()) {list.add(temp.toString());return;}//str 表示当前num对应的字符串//获取当前数字对应的字母字符串:String str = numString[digits.charAt(num) - '0'],//digits.charAt(num) 获取当前 num 指向的数字字符,通过减去字符 '0' 转换为对应的数组索引,得到当前数字对应的字符串。String str = numString[digits.charAt(num) - '0'];for (int i = 0; i < str.length(); i++) {temp.append(str.charAt(i));//递归,处理下一层backTraciking(digits, numString, num + 1);//剔除末尾的继续尝试temp.deleteCharAt(temp.length() - 1);}}}第二十二天的总算是结束了,直冲Day23!
相关文章:

第二十二天|回溯算法| 理论基础,77. 组合(剪枝),216. 组合总和III,17. 电话号码的字母组合
目录 回溯算法理论基础 1.题目分类 2.理论基础 3.回溯法模板 补充一个JAVA基础知识 什么时候用ArrayList什么时候用LinkedList 77. 组合 未剪枝优化 剪枝优化 216. 组合总和III 17. 电话号码的字母组合 回溯法的一个重点理解:细细理解这句话!…...

关闭IDM自动更新
关闭IDM自动更新 1 打开注册表2 找到IDM注册表路径 1 打开注册表 winR regedit 2 找到IDM注册表路径 计算机\HKEY_CURRENT_USER\Software\DownloadManager 双击LstCheck,把数值数据改为0 完成 感谢阅读...

Go 性能剖析工具 pprof 与 Graphviz 教程
在 Golang 开发中,性能分析是确保应用高效运行的重要环节。本文介绍如何使用 gin-contrib/pprof 在 Gin 应用中集成性能剖析工具,并结合 Graphviz 生成图形化的性能分析结果,如火焰图。这套流程帮助开发者更好地理解和优化 Go 应用的性能。 目…...

【题目解析】蓝桥杯23国赛C++中高级组 - 斗鱼养殖场
【题目解析】蓝桥杯23国赛C中高级组 - 斗鱼养殖场 题目链接跳转:点击跳转 前置知识: 了解过基本的动态规划。熟练掌握二进制的位运算。 题解思路 这是一道典型的状压动态规划问题。设 d p i , j dp_{i, j} dpi,j 表示遍历到第 i i i 行的时候&a…...

JavaScript可视化:探索顶尖的图表库
JavaScript可视化:探索顶尖的图表库 在这个被数据驱动的时代,你有没有想过,数据本身是如何变得有意义的?答案就是数据可视化。通过图表和图形,我们不仅可以看到数据,还可以感受到它,从而做出明…...

谷歌AI大模型Gemini API快速入门及LangChain调用视频教程
1. 谷歌Gemini API KEY获取及AI Studio使用 要使用谷歌Gemini API,首先需要获取API密钥。以下是获取API密钥的步骤: 访问Google AI Studio: 打开浏览器,访问Google AI Studio。使用Google账号登录,若没有账号…...

进入容器:掌控Docker的世界
进入容器:掌控Docker的世界 在这个快速发展的技术时代,你是否曾被Docker的庞大生态所吸引?那么,有没有想过在这个容器化的世界里,如何快速高效地“进入”这些隐藏在虚拟墙后的容器呢?容器就如同魔法箱,装载着应用与服务,而你,通过探索这些容器,能够更好地管理、排除…...

初始Linux(二)基础命令
前言: 之前那一篇我们已经介绍了一部分的基础命令,当然那只不过是九牛一毛,本篇我们继续介绍一些比较重要且需要掌握的基础命令。 mv命令: 其实这个命令有两个功能,一个是移动(剪切)文件&#…...

STM32 OLED
文章目录 前言一、OLED是什么?二、使用步骤1.复制 OLED.C .H文件1.1 遇到问题 2.统一风格3.主函数引用头文件3.1 oled.h 提供了什么函数 4.介绍显示一个字符的函数5. 显示十进制函数的讲解 三、使用注意事项3.1 配置符合自己的引脚3.2 花屏总结 前言 提示ÿ…...
伦敦金实时行情决策辅助!
在伦敦金实时交易的过程中,投资者主要依赖技术分析来辅助自己的投资决策。与基本面分析不同,技术分析侧重于研究金价的走势和市场行为,通过图表和技术指标来预测未来的市场走势。常用的技术分析方法包括: 趋势线和支撑阻力位&…...

Leetcode 746. 使用最小花费爬楼梯 入门dp C++实现
问题:Leetcode 746. 使用最小花费爬楼梯 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 请你…...

路由协议常见知识点
路由协议是网络通信的基础,主要负责在网络中传递数据包,并确保它们从源节点传递到目标节点。本文将介绍一些常见的路由协议知识点,包括路由协议的分类、特性、配置与管理以及常见问题。 一、路由协议的分类 距离矢量路由协议: R…...
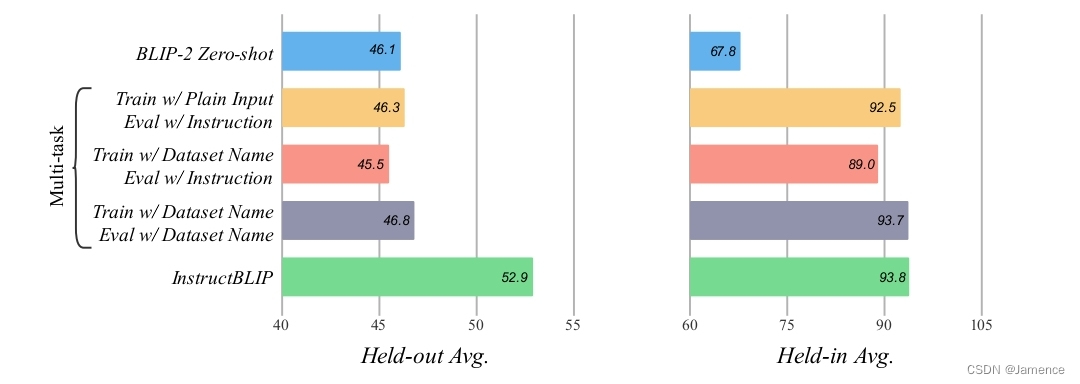
多模态大语言模型(MLLM)-InstructBlip深度解读
前言 InstructBlip可以理解为Blip2的升级版,重点加强了图文对话的能力。 模型结构和Blip2没差别,主要在数据集收集、数据集配比、指令微调等方面下文章。 创新点 数据集收集: 将26个公开数据集转换为指令微调格式,并将它们归类…...
:字符串)
网页前端开发之Javascript入门篇(7/9):字符串
Javascript字符串 什么是字符串? 答:其概念跟 Python教程 介绍的一样,只是语法上有所变化。 在 Javascript 中,一个字符串变量可以看做是其内置类String的一个实例(Javascript会自动包装)。 因此它拥有一…...

双登股份再战IPO:数据打架,实控人杨善基千万元股权激励儿子
撰稿|行星 来源|贝多财经 近日,双登集团股份有限公司(下称“双登股份”)递交招股书,准备在港交所主板上市,中金公司、建银国际、华泰国际为其联席保荐人。 贝多财经了解到,这并非双登股份首次向资本市场…...
)
4.Python 函数(函数的定义、函数的传入参数、函数的返回值、None 类型、函数说明文档、变量的作用域)
一、函数快速入门 1、函数概述 函数是组织好的,可重复使用的,用来实现特定功能的代码段 name "Hello World" name_length len(name)print(f"{name} 的长度为 {name_length}") # Hello World 的长度为 11len() 是Python 内置的函…...

【JavaEE】——文件IO
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:认识文件 1:文件的概念 2:文件的结构 3:文件路径…...

Python的pandas库基本操作(数据分析)
一、安装,导入 1、安装 使用包管理器安装: pip3 install pandas 2、导入 import pandas as pd as是为了方便引用起的别名 二、DateFrame 在Pandas库中,DataFrame 是一种非常重要的数据结构,它提供了一种灵活的方式来存储和…...
)
软件测试(平铺版本)
目录 黑盒测试: 定义: 示例:登录功能的黑盒测试 适合使用黑盒测试的情况 几种常见的黑盒测试方法: 1. 等价类划分(Equivalence Partitioning) 2. 边界值分析(Boundary Value Analysis) …...

树控件QTreeWidget
树控件跟表格控件类似,也可以有多列,也可以只有1列,可以有多行,只不过每一行都是一个QTreeWidgetItem,每一行都是一个可以展开的树 常用属性和方法 显示和隐藏标题栏 树控件只有水平标题栏 //获取和设置标题栏的显…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...
