JS中的Promise经典题目解析
这段代码很有代表性,涵盖了多个 JavaScript 知识点,特别是不同异步操作的执行优先级。
async function async1() {console.log('async1 start');await async2();console.log('async1 end');
}async function async2() {console.log('async2');
}console.log('script start');setTimeout(function() {console.log('setTimeout');
}, 0);async1();new Promise(function(resolve) {console.log('promise1');resolve();
}).then(function() {console.log('promise2');
});console.log('script end');
知识点总结:
async/await是基于 Promise 的语法糖,提供了更方便、直观的写法。- 当使用
async定义函数时,函数不会立即执行,只有在调用时才会开始执行。 - Promise 内部的代码是同步执行的,而
.then()中的代码是异步的。当使用async时,await expression;中的expression是要等待的 Promise 实例,其中的代码会同步执行,而await后面的代码相当于.then()的内容,因此是异步执行的。 async和 Promise 的代码执行优先级相同,都遵循先进先出(FIFO)原则,并且它们的优先级高于宏任务。setTimeout()属于宏任务。
执行顺序分析:
根据以上代码及解析,执行顺序为:
script startasync1 startasync2promise1script endpromise2setTimeout
相关文章:

JS中的Promise经典题目解析
这段代码很有代表性,涵盖了多个 JavaScript 知识点,特别是不同异步操作的执行优先级。 async function async1() {console.log(async1 start);await async2();console.log(async1 end); }async function async2() {console.log(async2); }console.log(s…...

【机器学习】金融预测 —— 风险管理与股市预测
我的主页:2的n次方_ 在金融领域,机器学习(ML)已经成为了不可或缺的工具。金融预测,尤其是风险管理和股市预测,涉及海量数据和复杂模式的分析,而这些正是机器学习擅长处理的领域。通过分析历…...

Bootstrap 5 分页组件使用教程
Bootstrap 5 分页组件使用教程 引言 Bootstrap 5 是一个流行的前端框架,它提供了一套丰富的组件和工具,用于快速开发响应式和移动优先的网页。分页组件是 Bootstrap 5 中用于分割长列表或数据集的重要部分,它可以帮助用户更容易地浏览内容。本文将详细介绍如何在您的项目中…...
Linux 安装 NVM 并配置 npm 加速,开发 node 项目不再愁
由于需要在 linux 机器上完成 node 项目的构建,需要安装 nodejs, 想着不同项目需要使用不同的版本,索性安装一下 nvm 吧,因为之前在 windows 上已经安装过 nvm-windows, 应该很容易上手,我尝试了官网提供的几种方式,最…...

MySQL 多条件查询
在 MySQL 中,多条件查询通常使用 WHERE 子句来指定多个条件。这些条件可以通过逻辑运算符(如 AND、OR、NOT)进行组合,以实现复杂的查询需求。以下是一些常见的多条件查询示例: 使用 AND 运算符 AND 运算符用于组合多…...

深度学习模型
1. 引言 在过去的十年间,深度学习的崛起引发了人工智能领域的革命,深刻影响了多个行业。深度学习是一种模仿人脑神经元的工作方式,通过多层神经网络进行数据处理与特征学习。其应用范围从简单的图像识别到复杂的自然语言处理、自动驾驶和医疗…...
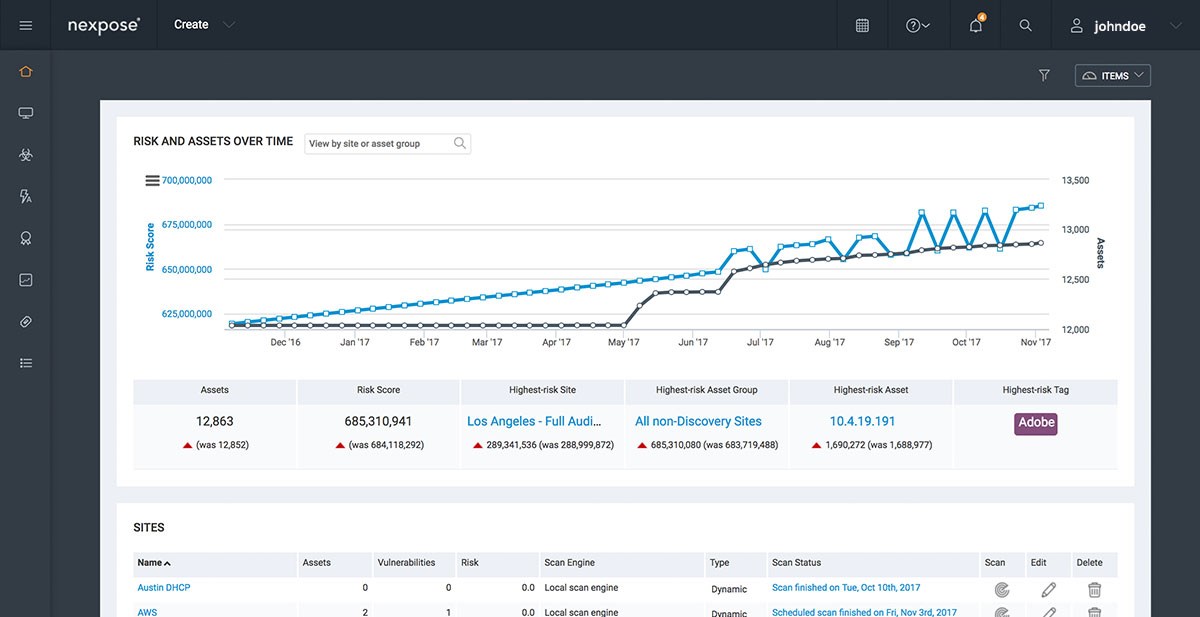
Nexpose 6.6.271 发布下载,新增功能概览
Nexpose 6.6.271 for Linux & Windows - 漏洞扫描 Rapid7 Vulnerability Management, release Sep 26, 2024 请访问原文链接:https://sysin.org/blog/nexpose-6/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.or…...
SimpleRAG-v1.0.3:增加文件对话功能
Kimi上有一个功能,就是增加文件之后对话,比如我有如下一个私有文档: 会议主题:《如何使用C#提升工作效率》 参会人员:张三、李四、王五 时间:2024.9.26 14:00-16:00 会议内容: 1. 自动化日常任…...

数学建模算法与应用 第7章 数理统计与方法
目录 7.1 参数估计与假设检验 Matlab代码示例:均值的假设检验 7.2 Bootstrap方法 Matlab代码示例:Bootstrap估计均值的置信区间 7.3 方差分析 Matlab代码示例:单因素方差分析 7.4 回归分析 Matlab代码示例:线性回归 7.5 基…...

【网络】洪水攻击防御指南
洪水攻击防御指南 摘要: 本文深入探讨了洪水攻击的概念、危害以及防御策略。通过Java技术实现,我们将学习如何通过编程手段来增强服务器的安全性。文章不仅提供了详细的技术解读,还包含了实用的代码示例和流程图,帮助读者构建一个…...

应对Redis大Key挑战:从原理到实现
在使用Redis作为缓存或数据存储时,开发者可能会遇到大Key(Big Key)问题。大Key是指在Redis中存储的单个键值对,其值的大小非常大,可能包含大量数据或占用大量内存。大Key问题会导致性能下降、内存消耗过多以及其他潜在…...

网络安全的全面指南
目录 网络安全的全面指南1. 引言2. 网络安全的基本概念3. 网络安全框架4. 常见网络安全攻击及案例4.1 病毒与恶意软件攻击案例4.2 钓鱼攻击案例4.3 DDoS 攻击案例 5. 网络安全最佳实践5.1 强密码策略5.2 定期更新和补丁管理5.3 数据备份与恢复策略 6. 企业网络安全策略6.1 安全…...

前端性能优化全面指南
前端性能优化是提升用户体验的关键,页面加载速度、响应时间和交互流畅度直接影响用户的留存率和满意度。以下是常用的前端性能优化方法,从网络层、资源加载、JavaScript 执行、渲染性能等方面进行全方位优化。 减少 HTTP 请求 合并文件:将多…...
)
JavaScript-API(倒计时的实现)
基础知识 1.时间对象的使用 1.1 实例化 要获取一个时间首先需要一个关键词new了实例化 const time new Date() 如果是获取具体的具体的时间 const time new Date(2024-6-1 16:06:44) 1.2 日期对象方法 方法作用说明getFullYear()获得年份获得4…...

【C++】——继承【上】
P. S.:以下代码均在VS2019环境下测试,不代表所有编译器均可通过。 P. S.:测试代码均未展示头文件stdio.h的声明,使用时请自行添加。 博主主页:Yan. yan. …...

SpringBoot 整合 阿里云 OSS图片上传
一、OOS 简介 阿里云OSS(Object Storage Service)是一种基于云存储的产品,适用于存储和管理各种类型的文件,包括图片、视频、文档等。 阿里云OSS具有高可靠性、高可用性和低成本等优点,因此被广泛应用于各种场景&…...

内核编译 设备驱动 驱动程序
内核编译 一、内核编译的步骤 编译步骤: (linux 内核源码的顶层目录下操作 ) 1. 拷贝默认配置到 .config cp config_mini2440_td35 .config 2. make menuconfig 内核配置 make menuconfig 3. make uImage make u…...

自由学习记录
约束的泛型通配符? Java中的泛型 xiaomi和byd都继承了car,但是只是这两个类是car的子类而已,而arraylist<xiaomi> ,arraylist<byd> 两个没有半毛钱继承关系 所以传入的参数整体,是car的list变形,里面的确都能存car…...

在 C# 中使用 LINQ 查询文件列表并找出最大文件
文章目录 1. 环境准备2. 创建项目3. 引入命名空间4. 示例代码5. 运行代码6. 进阶:异常处理7. 总结 在现代 C# 开发中,LINQ (Language Integrated Query) 提供了一种强大而优雅的方式来处理集合数据。本文将详细介绍如何使用 LINQ 查询文件系统中的文件&a…...

数学建模算法与应用 第6章 微分方程建模及其求解方法
目录 6.1 微分方程建模概述 6.2 发射卫星与三阶火箭建模 Matlab代码示例:火箭发射模拟 6.3 微分方程数值解法 Matlab代码示例:欧拉法与龙格-库塔法 6.4 放射性废料的处理 Matlab代码示例:放射性衰变 6.5 初值问题的Matlab数值求解 习…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
