查找与排序-交换排序
交换排序是基于“比较”和“交换”两种操作来实现的排序方法 。
由于选择“比较”的基准元素不同,可将交换排序分为以下两种:
- 冒泡排序
- 快速排序
一、冒泡排序
1.冒泡排序基本思想
因为其实现与气泡从水中往上冒的过程类似而得名。
每一趟的过程都是相邻两个元素比较,若为逆序,则交换两个元素,使关键字较小的元素如气泡一般逐渐往上“漂移”,直至最后冒出“水面”。直到某一趟排序过程中没有交换发生,说明序列已完全有序,排序完成。
2.算法步骤
假设待排序的n个数据元素存放在数组a中
(1)首先将第一个元素与第二个元素进行比较,若为逆序(a[0]>a[1]),则将两个元素交换,然后比较第二个元素和第三个元素。依次类推,直到第n-1个元素完成比较为止。上述过程称为第一次冒泡排序过程,其结果使得最大的记录被放在了最后一个记录的位置上。
(2)然后进行第二次冒泡排序过程,对前n-1个记录进行同样的操作,将次大的记录放在第n-1个记录的位置上。
(3)依此类推,直到某一次冒泡排序过程不再有交换发生,算法结束。
3.冒泡排序算法示例
例:设待排元素序列为{56,25,70,99,82,10,15,56},请给出冒泡排序法进行排序的过程。



4.算法代码
def bubble_sort2(self):data_len = len(self.data)for i in range(data_len-1, 0, -1): # 获得i号位置的正确值flag = Truefor j in range(0, i):if self.data[j+1].key <= self.data[j].key: self.data[j], self.data[j + 1] = self.data[j + 1], self.data[j] flag = Falseif flag:break
flag的作用:
- 冒泡算法的每一轮都是相邻元素a[0]与a[1], a[1]与a[2], ……比较,若为逆序则交换
- 只要某一轮发生了元素交换,则flag=False,说明此时整个数组还是无序状态,需要进行下一轮的相邻元素比较与交换
- 若某一轮相邻元素比较下来没有交换发生,则flag=True,说明此时整个序列已经有序了,以后轮次的比较就不再需要了
- 最好情况下,序列本身有序,则只需进行一轮比较,无交换
5.算法分析
(1)空间复杂度:在进行元素交换时,冒泡排序需要一个辅助空间临时存放元素,其空间复杂度为O(1)。
(2)时间复杂度:最好的情况下,序列本身是有序的。此时只需要一趟遍历进行n-1次相邻元素比较,无需交换操作。 最坏的情况下,初始序列为逆序,此时需要n-1趟遍历,第i趟遍历需要比较n-i次,总共比较n(n-1)/2次。每次比较都需要移动,因为每次移动都要通过辅助空间来进行,故每次移动次数都为3,总共移动次数3n(n-1)/2。所以综合考虑,冒泡排序算法的时间复杂度为O(n2)。
(3)其他方面:冒泡排序也可用于链式存储结构的序列排序,如果初始序列无序性强,数据元素多,则移动次数较多,此时不宜采用冒泡排序。
由于冒泡排序是顺次移动元素,所以不会破坏数值相同元素的初始次序,是一种稳定的排序方法。
二、快速排序
1.快速排序(划分交换排序)算法思想
(1)从数列中挑出一个元素,称为“基准”。
(2)重新排序数列,所有比基准值小的元素摆放在基准前面,所有大于或者等于基准值的元素摆在基准的后面,这个称为划分操作。在这个划分结束之后,该基准就处于数列的中间位置。 (3)递归地把小于基准值元素的子数列和大于基准值元素的子数列排序进行上述划分过程。
快速排序基本思想
- 将序列中的某一记录设置为枢轴(pivot),一趟排序将枢轴交换到其最终位置,所有小于枢轴的记录交换到枢轴的左边,所有大于等于枢轴的记录交换到枢轴的右边,这个过程称为一趟划分(partition)。
- 接下来对左子序列和右子序列分别快速排序,直至被排序子序列长度小于等于1为止。
- 分而治之思想,对整个序列的排序分解为对左子序列和右子序列的排序,是一种递归排序。
 一趟划分方法
一趟划分方法
- 对数组data中low~high范围内的元素进行一趟划分。
- 一般选取data[low]作为枢轴pivot。
- 在划分过程中始终保持下图所示的不变式,即pivot之后为小于pivot的区域A,紧接着是大于等于pivot的区域B,后面是i号位置开始的待处理区域。初始时,i=low+1,A和B区域的长度都为0。
 为了维持不变式,如果i号记录大于等于pivot,则i加1,即B区域长度增加1;否则,则将i号记录与B区域的最左记录进行交换。
为了维持不变式,如果i号记录大于等于pivot,则i加1,即B区域长度增加1;否则,则将i号记录与B区域的最左记录进行交换。- 为了方便交换,记录A、B区域的分界点last_small,设last_small为A区域的最右端位置。交换时,将last_small加1,i号记录与last_small位置记录交换,接着i加1。

当i超出high的范围,说明除了pivot之外的所有记录都已归入A区域或B区域,如图所示,此时,只需将pivot与last_small所指记录进行交换,即可达成一趟划分的目标。
 2.快速排序算法举例
2.快速排序算法举例
例:设待排数据元素序列为{26,67,67,9,6,43,82,10,54},请给出快速排序法进行排序的过程。
3.快速排序代码
一趟划分交换的代码
def partition(self, low, high):last_small = lowfor i in range(low + 1, high + 1):if self.data[i] < self.data[low]:last_small = last_small + 1self.swap(last_small, i)self.swap(low, last_small)return last_small
def swap(self, i, j): # 将i号和j号位置的记录交换self.data[i], self.data[j] = self.data[j], self.data[i]递归算法和接口方法
def recursive_quickSort(self, low, high):if low < high:self.swap(low,(low+high)//2)pivot_position = self.partition(low, high)self.recursive_quickSort(low, pivot_position - 1)self.recursive_quickSort(pivot_position + 1, high)def quick_sort(self):self.recursive_quickSort(0, len(self.data) - 1)
4.算法分析
(1)空间复杂度:快速排序是递归程序,每层递归调用过程需要一个栈来存放指针与参数,而快速排序最大递归调用的次数与递归树的深度一致,因此最好的情况下空间复杂度为O(log2n),最坏的情况下为O(n)。
(2)时间复杂度:平均情况O(n log2n) ,最坏情况,即每次划分过程产生的两个区间分别包含n-1个元素和1个元素的情况,比如待排序列已经有序的时候,其递归树为单分支树,这样必须进行n-1趟才能将所有元素定位,快速排序已经蜕化为简单排序的水平,其时间复杂度为O(n2)。

当对较大量数据构成的递增序列进行快速排序,且采用首元素为枢轴,可能发生递归调用栈溢出的错误。
为避免出现极端情况,可在进行一次划分之前进行“预处理”,即先对data[low].key、data[high].key和data[(low+high)//2].key进行相互比较,然后取关键字值“三者之中”的记录为枢轴记录。
当基准元素选择得当的时候(每次都选择中间元素为基准),每一趟排序都能将元素均匀地分割成两个长度相等的子序列,达到快速排序的最好情况,此时分割次数等于完全二叉树的深度log2n,另外,无论序列如何划分,全部比较次数都接近于n-1次,所以时间复杂度为O(nlog2n)。一般情况下,基准元素是随机分布的,序列分割次数接近于log2n,所以快速排序的平均时间复杂度为O(nlog2n)。
(3)其他方面:在所有同数量级的排序方法中,依平均时间复杂度,尤其是初始序列无序性强,数据元素比较多的时候,快速排序是目前性能最好的内部排序方法。在排序过程中需要序列的上下边界,所以不适合链式存储结构排序。由于数据元素移动的时候是不按顺序的,所以快速排序是一种不稳定的排序方法。
相关文章:

查找与排序-交换排序
交换排序是基于“比较”和“交换”两种操作来实现的排序方法 。 由于选择“比较”的基准元素不同,可将交换排序分为以下两种: 冒泡排序快速排序 一、冒泡排序 1.冒泡排序基本思想 因为其实现与气泡从水中往上冒的过程类似而得名。 每一趟的…...

数据结构与算法:高级数据结构与实际应用
目录 14.1 跳表 14.2 Trie树 14.3 B树与 B树 14.4 其他高级数据结构 总结 数据结构与算法:高级数据结构与实际应用 本章将探讨一些高级数据结构,这些数据结构在提高数据存取效率和解决复杂问题上起到重要作用。这些高级数据结构包括跳表࿰…...

【win11】终端/命令提示符/powershell美化
文章目录 1.设置字体1.1. 打开win11的终端/命令提示符/powershell其中之一1.2. 打开终端设置,修改所有终端默认字体为新宋体 2. 修改powershell背景色为蓝色 win11的默认终端/命令提示符/powershell主题风格让人感觉与win10撕裂太大,尤其是字体、背景色&…...
详解)
三元损失(Triplet Loss)详解
文章目录 前言一、三元损失的核心思想二、数学公式三、损失函数的解释四、三元损失的优势五、应用场景前言 三元损失(Triplet Loss)是一种广泛应用于度量学习(Metric Learning)中的损失函数,尤其在人脸识别、图像检索等任务中表现优异。三元损失的基本思想是通过定义一个…...

1. 解读DLT698.45-2017通信规约--预连接响应
国家电网有限公司企业标准,面向对象的用电信息数据交换协议DLT698.45-2017 为提高用电信息采集系统的业务适应性、采集效率、安全性和数据溯源性,规范用电信息数据交换协议的通信架构、数据链路层、应用层、接口类与对象标识,制定本标准。 …...

基于小波图像去噪的MATLAB实现
论文背景 数字图像处理(Digital Image Processing,DIP)是指用计算机辅助技术对图像信号进行处理的过程。数字图像处理最早出现于 20世纪50年代,随着过去几十年来计算机、网络技术和通信的快速发展,为信号处理这个学科领域的发展奠定了基础&a…...

[数据结构]栈的实现与应用
文章目录 一、引言二、栈的基本概念1、栈是什么2、栈的实现方式对比3、函数栈帧 三、栈的实现1、结构体定义2、初始化3、销毁4、显示5、数据操作 四、分析栈1、优点2、缺点 五、总结1、练习题2、源代码 一、引言 栈,作为一种基础且重要的数据结构,在计算…...

ESP32-C3 入门笔记04:gpio_key 按键 (ESP-IDF + VSCode)
1.GPIO简介 ESP32-C3是QFN32封装,GPIO引脚一共有22个,从GPIO0到GPIO21。 理论上,所有的IO都可以复用为任何外设功能,但有些引脚用作连接芯片内部FLASH或者外部FLASH功能时,官方不建议用作其它用途。 通过开发板的原…...

C语言(函数)—函数栈帧的创建和销毁
目录 前言 补充知识 一、函数线帧是什么? 二、函数线帧的实现(举例说明) 两数之和代码 编辑两数之和 汇编代码分析 执行第一条语句 执行第二条语句 执行第三条语句 执行第四、五、六条语句 执行第七条语句 执行第八、九、十条语句 执行第十…...

点餐小程序实战教程20广告管理
目录 1 创建数据源2 添加轮播容器3 创建变量4 绑定变量5 预览应用总结 一般餐厅需要有一些宣传,在我们的点餐页面可以在顶部加载广告位。广告主要是用轮播图的形式进行展示,本节我们介绍一下如果显示广告。 1 创建数据源 打开控制台,点击应用…...

市场上几个跨平台开发框架?
跨平台桌面应用开发框架是一种工具或框架,它允许开发者使用一种统一的代码库或语言来创建能够在多个操作系统上运行的桌面应用程序。传统上,开发者需要为每个操作系统编写不同的代码,使用不同的开发工具和语言。而跨平台桌面应用开发框架通过…...

同步和异步、引用、变量声明、全局变量
同步和异步 如果计算机足够快,任何资源的访问速度都像Cache一样,没有异步的必要。 编程语言的同步和异步 越早期的编程语言,支持语言级别的异步越欠缺。 JS提供某些操作的同步和异步函数,例如文件读取,fs.readFile和fs…...

2024年10月份实时获取地图边界数据方法,省市区县街道多级联动【附实时geoJson数据下载】
首先,来看下效果图 在线体验地址:https://geojson.hxkj.vip,并提供实时geoJson数据文件下载 可下载的数据包含省级geojson行政边界数据、市级geojson行政边界数据、区/县级geojson行政边界数据、省市区县街道行政编码四级联动数据࿰…...

@RequestMapping对不同参数的接收方式
1、简单参数 1、参数名与形参变量名相同,定义形参即可接收参数,且会自动进行类型转换。 RequestMapping("/simple")public String simpleParam(String name,int age){String username name;int userAge age;System.out.println(username&…...
算法_FaceBook_Location案例(附数据集下载链接))
机器学习_KNN(K近邻)算法_FaceBook_Location案例(附数据集下载链接)
Facebook_location_KNN 流程分析: 1.数据集获取(大型数据怎么获取? 放在电脑哪里? 算力怎么搞?) 2.基本数据处理(数据选取-确定特征值和目标值-分割数据集) 缩小数据范围 选择时间特征 去掉签到较少的地方 确定特征值和目标值 分割数据集 3.特征工程(特征预处理:标…...

【str_replace替换导致的绕过】
双写绕过 随便输入一个 usernameadmin&passwords 没有回显测试注入点 usernameadmin or 11%23&passwords 回显hello admin测试列数 usernameadmin order by 3%23&passwords测试回显位 usernameadmi union select 1,2,3%23&passwords 没有显示数据,推…...

如何用AI大模型提升挖洞速度
工具背景 越权漏洞在黑盒测试、SRC挖掘中几乎是必测的一项,但手工逐个测试越权漏洞往往会耗费大量时间,而自动化工具又存在大量误报, 基于此产生了AutorizePro, 那它是怎么提升效率一起来看看 AutorizePro 是一款专注于越权检测的 Burp 插件…...

两个数列问题
# 问题描述 给定长度分别为 n 和 m 的两个数列a[n]、b[m],和一个整数k。求|(a[i] - b[j])^2 - k^2|的最小值。 ## 输入格式 第一行有 2 个整数 n、m、k,分别表示数列 a、b 的长度,以及公式中的整数 k。 第二行有 n 个整数,表示…...
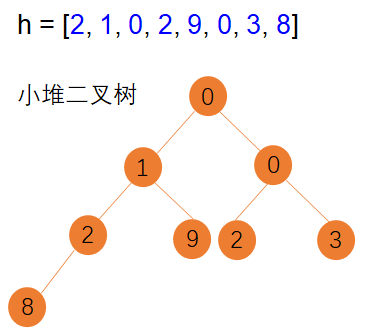
python中堆的用法
Python 堆(Headp) Python中堆是一种基于二叉树存储的数据结构。 主要应用场景: 对一个序列数据的操作基于排序的操作场景,例如序列数据基于最大值最小值进行的操作。 堆的数据结构: Python 中堆是一颗平衡二叉树&am…...

轮班管理新策略,提高效率与降低员工抱怨
良好轮班管理对企业关键,需提前计划、明确期望、保持灵活公平、加强沟通并利用轮班调度系统。ZohoPeople作为智能排班系统,提供轻松创建班次、自动更换、分配管理员、设置津贴及即时通知等功能,助力企业高效管理。 一、HR轮班管理的5大技巧 …...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

