R语言贝叶斯分层、层次（Hierarchical Bayesian）模型房价数据空间分析

原文链接：https://tecdat.cn/?p=38077

本文主要探讨了贝叶斯分层模型在分析区域数据方面的应用，以房价数据为例，详细阐述了如何帮助客户利用R进行模型拟合、分析及结果解读，展示了该方法在处理空间相关数据时的灵活性和有效性。（点击文末“阅读原文”获取完整代码数据）。

一、贝叶斯分层模型概述

贝叶斯分层模型（Banerjee, Carlin, and Gelfand 2004）可用于分析区域数据，当结果变量汇总到构成研究区域划分的各个区域时会产生这类数据。模型可被设定用于描述响应变量的变异性，其作为一些已知会影响结果的协变量的函数，同时还有随机效应来对协变量未解释的剩余变异进行建模。这提供了一种灵活且稳健的方法，使我们能够评估解释变量的影响、适应空间自相关，并量化所获估计值的不确定性。

常用的空间模型之一是Besag-York-Mollié（BYM）模型（Besag, York, and Mollié 1991）。假设 (Y_i) 是区域 (i = 1, \cdots, n) 观测到的结果，可使用正态分布进行建模。BYM模型设定如下：

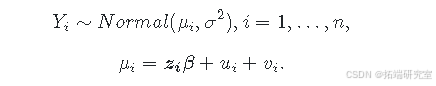
在此，固定效应 (z\_i\beta) 通过与区域 (i) 对应的截距和 (p) 个协变量的向量来表示，即 (z\_i=(1, z_{i1}, \cdots, z_{ip}))，系数向量为 (\beta = (\beta\_0, \cdots, \beta\_p)')。

该模型包含一个空间随机效应 (u\_i)，它用于解释结果之间的空间依赖性，表明彼此接近的区域可能具有相似的值，还有一个无结构可交换分量 (v\_i) 用于对不相关噪声进行建模。空间随机效应 (u_i) 可使用内在条件自回归模型（CAR）进行建模，该模型会根据特定的邻域结构对数据进行平滑处理。具体而言：

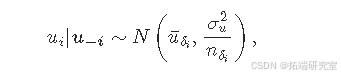
其中，(\overline{u}_{\delta\_i} = n\_{\delta\_i}^{-1}\sum\_{j \in \delta\_i}u\_j)，这里的 (\delta\_i) 和 (n\_{\delta\_i}) 分别表示区域 (i) 的邻居集合及其邻居数量。无结构分量 (v\_i) 被建模为独立同分布的正态变量，均值为零，方差为 (\sigma^2\_v)，即 (v\_i \sim N(0, \sigma^2_v))。

（一）贝叶斯推断与INLA

贝叶斯分层模型可通过多种方法进行拟合，如集成嵌套拉普拉斯近似（INLA）（Rue, Martino, and Chopin 2009）和马尔可夫链蒙特卡罗（MCMC）方法（Gelman et al. 2000）。INLA是一种在潜在高斯模型中进行近似贝叶斯推断的计算方法，它涵盖了广泛的模型，如广义线性混合模型、空间和时空模型等。INLA通过结合解析近似和数值积分来获得参数的近似后验分布，与MCMC方法相比速度非常快。

二、房价的空间建模示例

（一）波士顿的房价数据

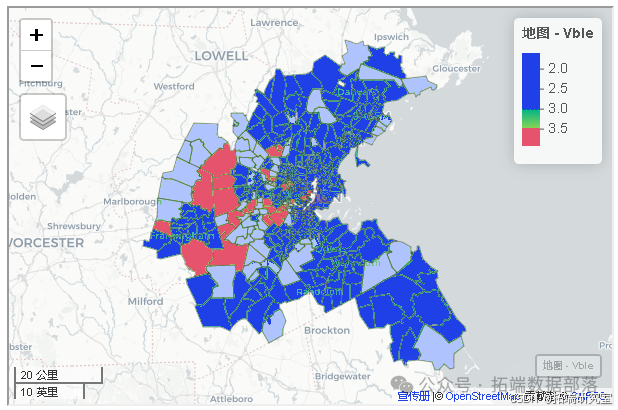
该数据集包含了506个波士顿人口普查区的住房数据，包括自有住房中位数价格（以1000美元为单位，变量名为MEDV）、人均犯罪率（CRIM）和每户平均房间数（RM）。我们创建一个名为vble的变量，其值为中位数价格的对数，并使用mapview对该变量进行地图绘制。该地图表明房价在西部较高，且房价与相邻区域的房价相关。

我们将使用人均犯罪率（CRIM）和每户平均房间数（RM）作为协变量来对中位数价格的对数进行建模。图9.2展示了使用GGally包（Schloerke et al. 2021）的  `[ggpairs()](https://ggobi.github.io/ggally/reference/ggpairs.html "ggpairs()")` 函数可视化的变量对之间的关系。我们观察到房价对数与犯罪率之间呈负相关，与平均房间数之间呈正相关。

---

点击标题查阅往期内容

课程视频|R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例

左右滑动查看更多

01

02

03

04

library(GGally)
ggpairs(data = map, columns = c("vble", "CRIM", "RM"))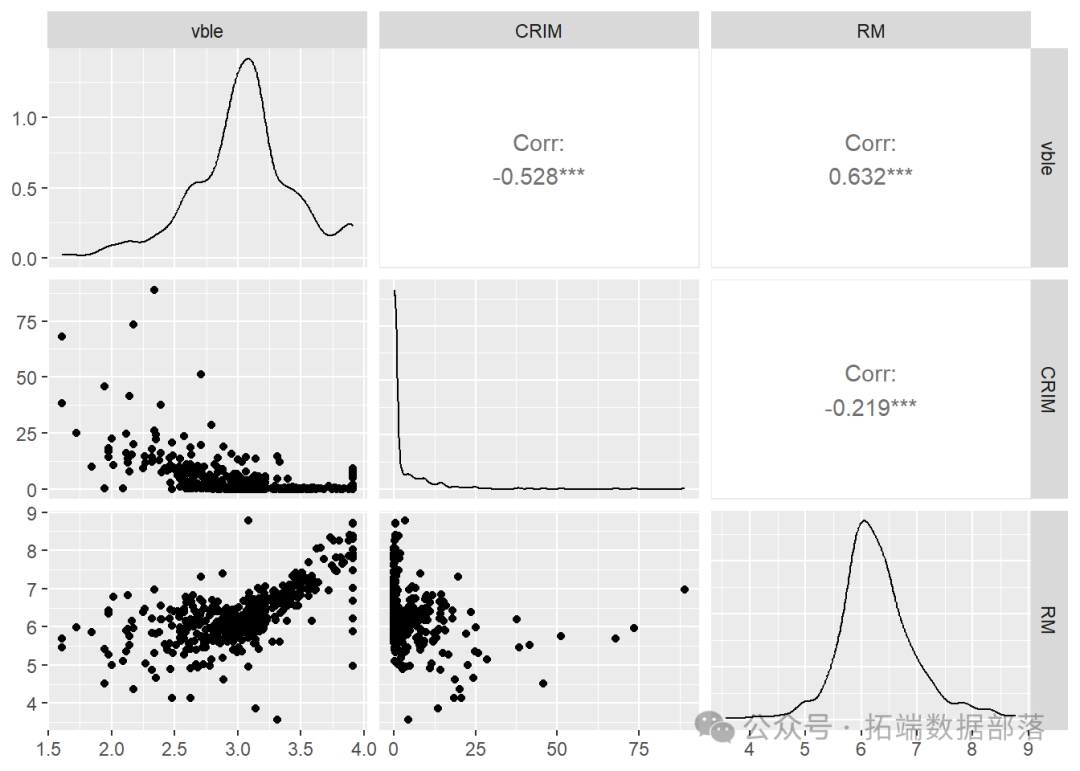

（二）模型设定

设 (Y\_i) 为区域 (i)（(i = 1, \cdots, n)）的房价对数。我们拟合一个BYM模型，将 (Y\_i) 作为响应变量，犯罪率和房间数作为协变量，模型如下：

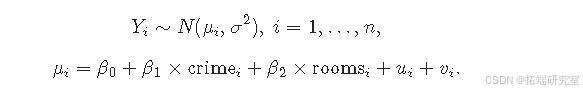
在此，(\beta\_0) 是截距，(\beta\_1) 和 (\beta\_2) 分别代表协变量犯罪率和房间数的系数。(u\_i) 是使用CAR结构建模的空间结构化效应，(u\_i|u\_{-i} \sim N(\overline{u}_{\delta\_i}, \sigma^2\_u n_{\delta\_i}))。(v\_i) 是建模为 (v\_i \sim N(0, \sigma^2\_v)) 的无结构效应。

（三）邻域矩阵

在模型中，空间随机效应 (u_i) 需要使用邻域结构来指定。在此，我们假设如果两个区域共享公共边界则它们是邻居，并使用spdep包（Bivand 2022）的函数来创建邻域结构。首先，我们使用  `[poly2nb()](https://r-spatial.github.io/spdep/reference/poly2nb.html "poly2nb()")` 函数基于具有连续边界的区域创建一个邻居列表。列表 nb 的每个元素代表一个区域，并包含其邻居的索引。例如，nb[[1]] 包含区域1的邻居。

然后，我们使用  `[nb2INLA()](https://r-spatial.github.io/spdep/reference/nb2INLA.html "nb2INLA()")` 函数将 nb 列表转换为一个名为 map.adj 的文件，该文件包含了R-INLA所需的邻域矩阵表示形式。map.adj 文件保存在当前工作目录中，可通过  `[getwd()](https://rdrr.io/r/base/getwd.html "getwd()")` 函数获取。然后，我们使用R-INLA的  `[inla.read.graph()](https://rdrr.io/pkg/INLA/man/read.graph.html "inla.read.graph()")` 函数读取 map.adj 文件，并将其存储在对象 g 中，稍后我们将使用该对象通过R-INLA来指定空间模型。

（四）模型公式与 inla() 调用

我们通过包含响应变量、~ 符号以及固定效应和随机效应来指定模型公式。默认情况下有一个截距，所以我们不需要在公式中包含它。在公式中，随机效应通过  `[f()](https://rdrr.io/pkg/INLA/man/f.html "f()")` 函数来指定。该函数的第一个参数是一个索引向量，用于指定适用于每个观测值的随机效应元素，第二个参数是模型名称。对于空间随机效应 (u_i)，我们使用 model = "besag" 并将邻域矩阵设为 g。选项 scale.model = TRUE 用于使具有不同CAR先验的模型的精度参数具有可比性（Freni-Sterrantino, Ventrucci, and Rue 2018）。对于无结构效应 (v_i)，我们选择 model = "iid"。随机效应的索引向量分别为 re_u 和 re_v，它们是为 (u\_i) 和 (v\_i) 创建的，这些向量的值为 (1, \cdots, n)，其中 (n) 是区域数量。

map$re_u <- 1:nrow(map)
map$re_v <- 1:nrow(map)
formula <- vble ~ CRIM + RM +  f(re\_u, model = "besag", graph = g, scale.model = TRUE) +  f(re\_v, model = "iid")

需要注意的是，在R-INLA中，BYM模型也可通过 model = "bym" 来指定，这将同时包含空间和无结构组件。或者，我们也可以使用BYM2模型（Simpson et al. 2017），它是BYM模型的一种新参数化形式，使用了缩放后的空间组件 (u^_) 和无结构组件 (v^_)：

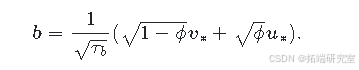
在该模型中，精度参数 (\tau_b > 0) 控制着 (u^_) 和 (v^_) 加权和的边际方差贡献。混合参数 (0 \leq \phi \leq 1) 衡量了空间组件 (u^*) 所解释的边际方差比例。因此，当 (\phi = 1) 时，BYM2模型等同于仅含空间的模型，当 (\phi = 0) 时，等同于仅含无结构空间噪声的模型（Riebler et al. 2017）。使用BYM2组件的模型公式指定如下：

（五）结果分析

1. 模型拟合结果概述

通过调用 inla() 函数并传入相应的公式、分布族、数据以及使用 R-INLA 中的默认先验信息完成模型拟合后，得到的结果对象 res 包含了模型的拟合情况。

我们可以使用 summary(res) 函数来获取拟合模型的概要信息。其中，res$summary.fixed 包含了固定效应的概要内容，如下所示：

res$summary.fixed

其输出结果如下：

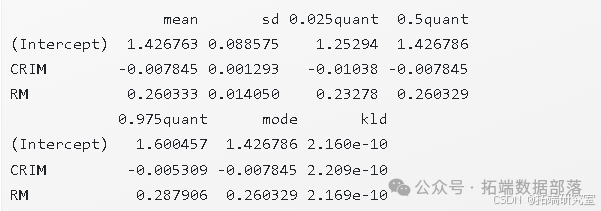
从上述结果中我们可以观察到，截距项  的估计值为 ，其  可信区间为 (, )。而对于协变量犯罪率（CRIM），其系数估计值  为 ，对应的  可信区间为 (, )，这表明犯罪率与房价之间存在显著的负相关关系。房间数（RM）的系数  为 ， 可信区间为 (, )，这意味着房间数与房价之间存在显著的正相关关系。由此可见，犯罪率和房间数这两个因素在解释房价的空间分布模式方面都起着重要作用。

2. 响应变量后验分布概要

我们还可以通过输入 res$summary.fitted.values 来获取每个区域响应变量  的后验分布概要信息。其中，“mean” 列表示后验均值，“0.025quant” 列和 “0.975quant” 列分别表示  可信区间的下限和上限，它们代表了所获得估计值的不确定性程度。其输出结果如下：

summary(res$summary.fitted.values)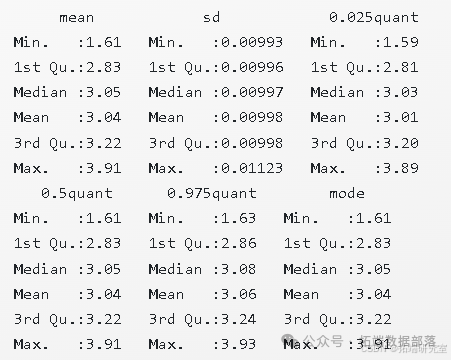

基于上述结果，我们可以进一步创建包含后验均值（PM）以及  可信区间下限（LL）和上限（UL）的变量，具体代码如下：

# 后验均值和95%可信区间
map$PM <- res$summary.fitted.values\[, "mean"\]
map$LL <- res$summary.fitted.values\[, "0.025quant"\]
map$UL <- res$summary.fitted.values\[, "0.975quant"\]

3. 绘制相关变量地图

随后，我们使用 mapview 包来创建这些变量的地图。在创建地图过程中，我们为这三张地图指定了一个通用的图例，并使用一个弹出式表格，其中包含区域名称、房价对数、协变量以及后验均值和  可信区间等信息。同时，我们利用 leafsync 包中的 sync() 函数来绘制同步地图，具体步骤如下：

首先，设置通用图例的取值范围：

# 通用图例
at <- seq(min(c(map$PM, map$LL, map$UL)),max(c(map$PM, map$LL, map$UL)),length.out = 8)

然后，创建弹出式表格：

# 弹出式表格
popuptable <- leafpop::popupTable(dplyr::mutate_if(map,is.numeric, round, digits = 2),zcol = c("TOWN", "vble", "CRIM", "RM", "PM", "LL", "UL"),row.numbers = FALSE, feature.id = FALSE)

接着，分别创建三张地图对象 m1、m2 和 m3，分别对应后验均值、下限和上限的可视化：

m1 <- mapview(map, zcol = "PM", map.types = "CartoDB.Positron",at = at, popup = popuptable)
m2 <- mapview(map, zcol = "LL", map.types = "CartoDB.Positron",at = at, popup = popuptable)
m3 <- mapview(map, zcol = "UL", map.types = "CartoDB.Positron",at = at, popup = popuptable)

最后，将这三张地图进行同步绘制并展示：

其生成的地图可参考下图

4. 获取原始房价规模的估计值

为了得到原始房价规模的估计值，我们需要对房价对数的估计值进行转换。首先，使用 inla.tmarginal() 函数来获取价格的边际分布，通过 exp(log(price)) 的方式进行转换。然后，再利用 inla.zmarginal() 函数来获取这些边际分布的概要信息。最后，创建变量 PMoriginal、LLoriginal 和 ULoriginal，它们分别对应原始房价后验分布的后验均值以及  可信区间的下限和上限，具体代码如下：

# 对第一个区域的边际分布进行转换（示例）
# inla.tmarginal(function(x) exp(x),
#                res$marginals.fitted.values\[\[1\]\])# 对所有边际分布进行转换
marginals <- lapply(res$marginals.fitted.values,FUN = function(marg){inla.tmarginal(function(x) exp(x), marg)})# 获取边际分布的概要信息
marginals_summaries <- lapply(marginals,FUN = function(marg){inla.zmarginal(marg)})# 后验均值和95%可信区间
map$PMoriginal <- sapply(marginals_summaries, '\[\[', "mean") 
map$LLoriginal <- sapply(marginals_summaries, '\[\[', "quant0.025")
map$ULoriginal <- sapply(marginals_summaries, '\[\[', "quant0.975")

同样地，我们可以基于这些变量创建地图来展示原始房价估计值及其  可信区间，以便更好地理解波士顿房价的空间分布模式以及估计值的不确定性。具体创建地图的步骤与上述类似，只是这里使用的是 PMoriginal、LLoriginal 和 ULoriginal 变量，生成的地图可参考下图

通过上述一系列的分析和可视化操作，我们能够较为全面地了解基于贝叶斯分层模型对波士顿房价数据进行建模分析的结果，以及各因素对房价空间分布的影响和估计值的不确定性情况。

本文中分析的数据、代码分享到会员群，扫描下面二维码即可加群！ 

---

资料获取

在公众号后台回复“领资料”，可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”

获取全文完整代码数据资料。

本文选自《R语言基于贝叶斯分层、层次模型的房价数据空间分析》。

点击标题查阅往期内容

课程视频|R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例

R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

python贝叶斯随机过程：马尔可夫链Markov-Chain，MC和Metropolis-Hastings，MH采样算法可视化

Python贝叶斯推断Metropolis-Hastings（M-H）MCMC采样算法的实现

Metropolis Hastings采样和贝叶斯泊松回归Poisson模型

Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列

R语言RSTAN MCMC：NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据

R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析

R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型

R语言贝叶斯MCMC：用rstan建立线性回归模型分析汽车数据和可视化诊断

R语言贝叶斯MCMC：GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例

R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数

R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数

R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病

R语言中贝叶斯网络（BN）、动态贝叶斯网络、线性模型分析错颌畸形数据

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

Python贝叶斯回归分析住房负担能力数据集

R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析

Python用PyMC3实现贝叶斯线性回归模型

R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型

R语言Gibbs抽样的贝叶斯简单线性回归仿真分析

R语言和STAN,JAGS：用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据

R语言基于copula的贝叶斯分层混合模型的诊断准确性研究

R语言贝叶斯线性回归和多元线性回归构建工资预测模型

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言stan进行基于贝叶斯推断的回归模型

R语言中RStan贝叶斯层次模型分析示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样

R语言贝叶斯推断与MCMC：实现Metropolis-Hastings 采样算法示例

R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化

视频：R语言中的Stan概率编程MCMC采样的贝叶斯模型

R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计