数据结构之线段树
线段树
线段树(Segment Tree)是一种高效的数据结构,广泛应用于计算机科学和算法中,特别是在处理区间查询和更新问题时表现出色。以下是对线段树的详细解释:
一、基本概念
线段树是一种二叉搜索树,是算法竞赛中常用的用来维护 区间信息 的数据结构。线段树可以在 ![]()
的时间复杂度内实现单点修改、区间修改、区间查询(区间求和,求区间最大值,求区间最小值)等操作。
原理其实是分治思想。它将整个区间划分成一些单元区间,具有对数级别的高度,从而保证了高效的查询和更新操作。
二、基本结构
- 根结点:代表整个区间。
- 内部结点:每个内部结点都代表一个区间,并将其划分为左右两个子区间,分别由左孩子和右孩子表示。
- 叶结点:代表单元区间,每个叶结点对应原始数据中的一个元素。
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。
三、示例应用
假设有一个长度为N的数组a,需要频繁地查询任意区间[l,r]的最小值和以及更新数组中的某个元素。使用线段树可以高效地解决这些问题。以下是一个简单的线段树实现示例(以Python代码表示):
class SegmentTree: def __init__(self, nums): self.nums = nums self.n = len(nums) # 初始化线段树,大小为4倍的原数组长度,因为线段树是完全二叉树 self.tree = [float('inf')] * (4 * self.n) self.build_tree(0, 0, self.n - 1) def build_tree(self, tree_index, l, r): # 如果到达了叶节点 if l == r: self.tree[tree_index] = self.nums[l] return # 计算左右子节点的索引 left_child = 2 * tree_index + 1 right_child = 2 * tree_index + 2 # 递归构建左右子树 mid = (l + r) // 2 self.build_tree(left_child, l, mid) self.build_tree(right_child, mid + 1, r) # 当前节点的值是其左右子节点值的最小值 self.tree[tree_index] = min(self.tree[left_child], self.tree[right_child]) def query(self, l, r): return self.query_tree(0, 0, self.n - 1, l, r) def query_tree(self, tree_index, seg_l, seg_r, query_l, query_r): # 如果查询区间完全包含了当前线段树节点代表的区间 if query_l <= seg_l and seg_r <= query_r: return self.tree[tree_index] # 如果查询区间与当前线段树节点代表的区间没有交集 if query_l > seg_r or query_r < seg_l: return float('inf') # 计算左右子节点的索引 left_child = 2 * tree_index + 1 right_child = 2 * tree_index + 2 # 递归查询左右子树,并取最小值 mid = (seg_l + seg_r) // 2 left_min = self.query_tree(left_child, seg_l, mid, query_l, query_r) right_min = self.query_tree(right_child, mid + 1, seg_r, query_l, query_r) return min(left_min, right_min) def update(self, index, value): self.update_tree(0, 0, self.n - 1, index, value) def update_tree(self, tree_index, seg_l, seg_r, index, value): # 如果到达了叶节点 if seg_l == seg_r: self.nums[index] = value self.tree[tree_index] = value return # 计算左右子节点的索引 left_child = 2 * tree_index + 1 right_child = 2 * tree_index + 2 # 递归更新左右子树 mid = (seg_l + seg_r) // 2 if index <= mid: self.update_tree(left_child, seg_l, mid, index, value) else: self.update_tree(right_child, mid + 1, seg_r, index, value) # 当前节点的值是其左右子节点值的最小值 self.tree[tree_index] = min(self.tree[left_child], self.tree[right_child]) # 示例用法
nums = [1, 3, 2, 7, 9, 11]
seg_tree = SegmentTree(nums) # 查询区间[1, 3]的最小值
print(seg_tree.query(1, 3)) # 输出: 2 # 更新索引2处的值为0
seg_tree.update(2, 0) # 再次查询区间[1, 3]的最小值
print(seg_tree.query(1, 3)) # 输出: 0相关文章:
数据结构之线段树
线段树 线段树(Segment Tree)是一种高效的数据结构,广泛应用于计算机科学和算法中,特别是在处理区间查询和更新问题时表现出色。以下是对线段树的详细解释: 一、基本概念 线段树是一种二叉搜索树,是算法竞…...

vue 快速入门
文章目录 一、插值表达式 {{}}二、Vue 指令2.1 v-text 和 v-html:2.2 v-if 和 v-show:2.3 v-on:2.4 v-bind 和 v-model:2.5 v-for: 三、生命周期四、Vue 组件库 Element五、Vue 路由 本文章适用于后端人员,…...
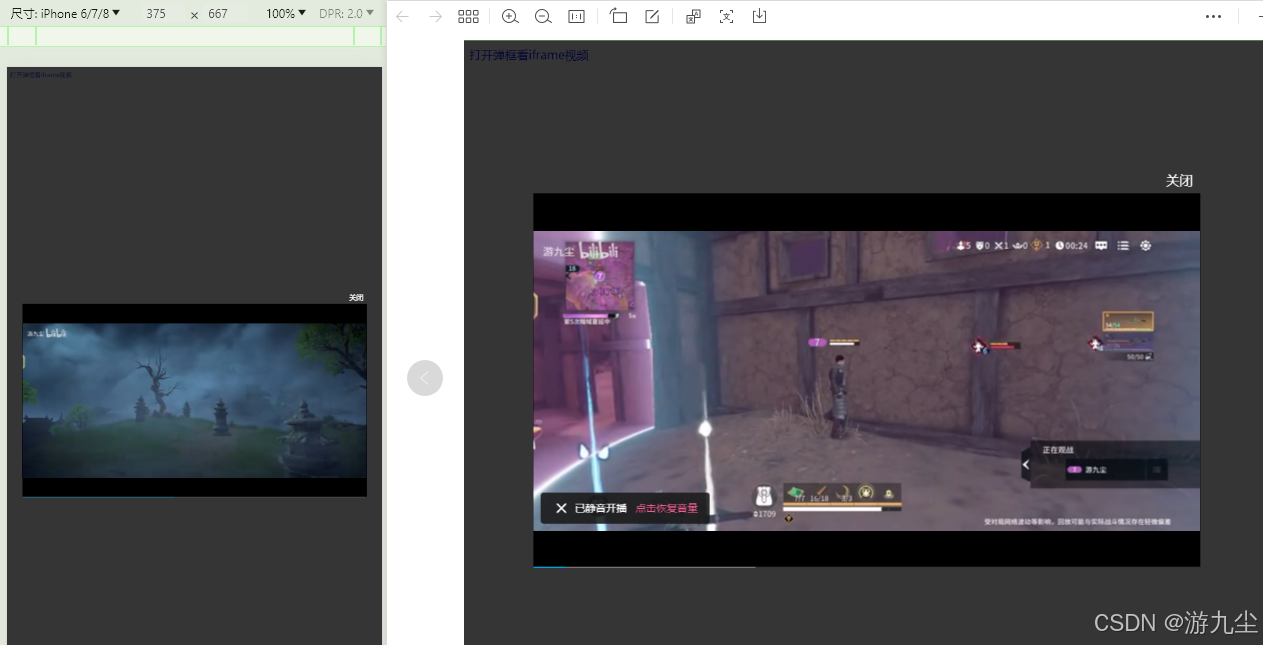
iframe视频宽度高度自适应( pc+移动都可以用,jq写法 )
注意:要引入jquery 可以直接使用弹框播放iframe 一、创建 index.html <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style>.modal {/* 默认隐藏 */display: none;position: fixed;z-i…...

Observability:OpenTelemetry Elastic 分发简介
作者:来自 Elastic Alexander Wert•Miguel Luna•Bahubali Shetti Elastic 自豪地推出了 Elastic Distributions of OpenTelemetry (EDOT),其中包含 Elastic 版本的 OpenTelemetry Collector 和多种语言 SDK,如 Python、Java、.NET 和 NodeJ…...

golang的RSA加密解密
参考:https://blog.csdn.net/lady_killer9/article/details/118026802 1.加密解密工具类PasswordUtil.go package utilimport ("crypto/rand""crypto/rsa""crypto/x509""encoding/pem""fmt""log"&qu…...

深度学习-梯度消失/爆炸产生的原因、解决方法
在深度学习模型中,梯度消失和梯度爆炸现象是限制深层神经网络有效训练的主要问题之一,这两个现象从本质上来说是由链式求导过程中梯度的缩小或增大引起的。特别是在深层网络中,若初始梯度在反向传播过程中逐层被放大或缩小,最后导…...
模式概述)
MVC(Model-View-Controller)模式概述
MVC(Model-View-Controller)是一种设计模式,最初由 Trygve Reenskaug 在 1970 年代提出,并在 Smalltalk 编程环境中得到了广泛应用。MVC 模式旨在实现用户界面和业务逻辑的分离,以增强应用程序的可维护性、可扩展性和复…...

数据结构 —— 红黑树
目录 1. 初识红黑树 1.1 红黑树的概念 1.2 红⿊树的规则 1.3 红黑树如何确保最长路径不超过最短路径的2倍 1.4 红黑树的效率:O(logN) 2. 红黑树的实现 2.1 红黑树的基础结构框架 2.2 红黑树的插⼊ 2.2.1 情况1:变色 2.2.2 情况2:单旋变色 2.2…...

《功能高分子学报》
《功能高分子学报》 中国标准连续出版物号:CN 31-1633/O6,国际标准连续出版物号:ISSN 1008-9357,邮发代号:4-629,刊期:双月刊。 《功能高分子学报》主要刊登功能高分子和其他高分子领域具有创新意义的学术…...

Linux特种文件系统--tmpfs文件系统
tmpfs类似于RamDisk(只能使用物理内存),使用虚拟内存(简称VM)子系统的页面存储文件。tmpfs完全依赖VM,遵循子系统的整体调度策略。说白了tmpfs跟普通进程差不多,使用的都是某种形式的虚拟内存&a…...

《基于STMF103的FreeRTOS内核移植》
目录 1.FreeRTOS资料下载与出处 1.1官网下载,网址:www.freertos.org 1.2在正点原子官网,任意STM32F1的开发板资料A盘里, 2.FreeRTOS移植重要文件讲解 2.1 FreeRTOS与FreeRTOS-Plus文件夹 2.2 Demo、Lincence、Source ●Demo文件…...

一七二、Vue3性能优化方式
Vue 3 的性能优化相较于 Vue 2 有了显著提升,利用新特性和改进方法可以更高效地构建和优化应用。以下是 Vue 3 的常见性能优化方法及示例。 1. 使用组合式 API (Composition API) Vue 3 引入的组合式 API,通过逻辑拆分和复用来实现更高效的代码组织和性…...

软件测试--BUG篇
博主主页: 码农派大星. 数据结构专栏:Java数据结构 数据库专栏:MySQL数据库 JavaEE专栏:JavaEE 软件测试专栏:软件测试 关注博主带你了解更多知识 目录 1. 软件测试的⽣命周期 2. BUG 1. BUG 的概念 2. 描述bug的要素 3.bug级别 4.bug的⽣命周期 5 与开发产⽣争执怎…...

Scikit-learn和Keras简介
一,Scikit-learn是一个开源的机器学习库,用于Python编程语言。它建立在NumPy、SciPy和matplotlib这些科学计算库之上,提供了简单有效的数据挖掘和数据分析工具。Scikit-learn库包含了许多用于分类、回归、聚类和降维的算法,包括支…...

python在word的页脚插入页码
1、插入简易页码 import win32com.client as win32 from win32com.client import constants import osdoc_app win32.gencache.EnsureDispatch(Word.Application)#打开word应用程序 doc_app.Visible Truedoc doc_app.Documents.Add() footer doc.Sections(1).Footers(cons…...

Java面试题十四
一、Java中的JNI(Java Native Interface)是什么?它有什么用途? Java中的JNI(Java Native Interface)是Java提供的一种编程框架,它允许Java代码与本地(Native)代码&#x…...

yarn : 无法加载文件,未对文件 进行数字签名。无法在当前系统上运行该脚本。
执行这个命令时报错:yarn --registryhttps://registry.npm.taobao.org yarn : 无法加载文件 C:\Users\Administrator\AppData\Roaming\npm\yarn.ps1。未对文件 C:\Users\Administ rator\AppData\Roaming\npm\yarn.ps1 进行数字签名。无法在当前系统上运行该脚本。有…...

Hadoop——HDFS
什么是HDFS HDFS(Hadoop Distributed File System)是Apache Hadoop的核心组件之一,是一个分布式文件系统,专门设计用于在大规模集群上存储和管理海量数据。它的设计目标是提供高吞吐量的数据访问和容错能力,以支持大数…...

计算机的一些基础知识
文章目录 编程语言 程序 所谓程序,就是 一组指令 以及 这组指令要处理的数据。狭义上来说,程序对我们来说,通常表现为一组文件。 程序 指令 指令要处理的数据。 编程语言发展 机器语言:0、1 二进制构成汇编语言:…...

学习RocketMQ(记录了个人艰难学习RocketMQ的笔记)
一、部署单点RocketMQ Docker 部署 RocketMQ (图文并茂超详细)_docker 部署rocketmq-CSDN博客 这个博主讲的很好,可食用,替大家实践了一遍 二、原理篇 为什么使用RocketMQ: 为什么选择RocketMQ | RocketMQ 关于一些原理,感觉…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
