2023 icpc杭州(M,J,D,G,H)
文章目录
- [M. V-Diagram](https://codeforces.com/gym/104976/problem/M)
- [J. Mysterious Tree](https://codeforces.com/gym/104976/problem/J)
- [D.Operator Precedence](https://codeforces.com/gym/104976/problem/D)
- [G. Snake Move](https://codeforces.com/gym/104976/problem/G)
- [H. Sugar Sweet II](https://codeforces.com/gym/104976/problem/H)
M. V-Diagram
题意:
给一个V图,求一个连续子序列平均值最大的V图
首先,要保证是V字形,最小的和左右两个是一定要保留的,然后,如果某个小的选了,那么选比它大的肯定是提高平均值的,所以把V字形的一边全选了,至于为什么不把另一边也一起选了,是因为,有可能已经选的一边数非常大,而另一边数非常小,那么会拉低平均值,同理,只选另一边,以及选择整个V字形
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=3e5+10;
int a[N];
int n;
void solve() {cin>>n;int minn=2e9;for(int i=1;i<=n;i++) cin>>a[i],minn=min(minn,a[i]);double ans=0;int idx;for(int i=1;i<=n;i++){if(a[i]==minn){idx=i;break;}}double sum=0;for(int i=1;i<=idx+1;i++) sum+=a[i];ans=max(ans,sum/(idx+1));sum=0;for(int i=n;i>=idx-1;i--) sum+=a[i];ans=max(ans,sum/(n-idx+2));sum=0;for(int i=1;i<=n;i++) sum+=a[i];ans=max(ans,sum/n);printf("%.10f\n",ans);
}
signed main() {
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}
J. Mysterious Tree
题意:
一棵树,可能是链或者菊花,每次询问一条边存在性,确定是链还是菊 花。询问次数⌈n 2⌉+3
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
void solve() {cin>>n;if(n%2==0){for(int i=1;i<=n;i+=2){cout<<"? "<<i<<' '<<i+1<<endl;cout.flush();int x;cin>>x;if(x==1){if(i==1){cout<<"? "<<1<<' '<<3<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"? "<<1<<' '<<4<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"! "<<2<<endl;cout.flush();return;}else{cout<<"! "<<1<<endl;cout.flush();return;}}else{cout<<"? "<<2<<' '<<3<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"? "<<2<<' '<<4<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"! "<<2<<endl;cout.flush();return;}}}}else{cout<<"? "<<i<<' '<<1<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"? "<<i<<' '<<2<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"! "<<2<<endl;cout.flush();return;}else{cout<<"! "<<1<<endl;cout.flush();return;}}else{cout<<"? "<<i+1<<' '<<1<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"? "<<i+1<<' '<<2<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"! "<<2<<endl;cout.flush();return;}}}}}}cout<<"! "<<1<<endl;cout.flush();}else{for(int i=1;i<=n-1;i+=2){cout<<"? "<<i<<' '<<i+1<<endl;cout.flush();int x;cin>>x;if(x==1){if(i==1){cout<<"? "<<1<<' '<<3<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"? "<<1<<' '<<4<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"! "<<2<<endl;cout.flush();return;}else{cout<<"! "<<1<<endl;cout.flush();return;}}else{cout<<"? "<<2<<' '<<3<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"? "<<2<<' '<<4<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"! "<<2<<endl;cout.flush();return;}}}}else{cout<<"? "<<i<<' '<<1<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"? "<<i<<' '<<2<<endl;cout.flush();int x;cin>>x;if(x==1){cout<<"! "<<2<<endl;cout.flush();return;}else{cout<<"! "<<1<<endl;cout.flush();return;}}else{cout<<"? "<<i+1<<' '<<1<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"? "<<i+1<<' '<<2<<endl;cout.flush();int x;cin>>x;if(x==0){cout<<"! "<<1<<endl;cout.flush();return;}else{cout<<"! "<<2<<endl;cout.flush();return;}}}}}}cout<<"? "<<n<<' '<<1<<endl;cout.flush();int x;cin>>x;cout<<"? "<<n<<' '<<2<<endl;cout.flush();int y;cin>>y;cout<<"? "<<n<<' '<<3<<endl;cout.flush();int z;cin>>z;if(x==1&&y==1&&z==1){cout<<"! "<<2<<endl;cout.flush();}else {cout<<"! "<<1<<endl;cout.flush();}}
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}
D.Operator Precedence
题意:
构造2*n个数,满足
( a 1 a_1 a1 a 2 a_2 a2)+( a 3 a_3 a3 a 4 a_4 a4)+…( a 2 n − 1 a_{2n-1} a2n−1 a 2 n a_{2n} a2n)= a 1 a_1 a1( a 2 a_2 a2+ a 3 a_3 a3)( a 4 a_4 a4+ a 5 a_5 a5)…( a 2 n − 2 a_{2n-2} a2n−2+ a 2 n − 1 a_{2n-1} a2n−1) a 2 n a_{2n} a2n
且最终结果不等于0
构造题,往往用最特殊,最简单的,自己构造,肯定简单化而不是复杂化
由于中间全部乘起来,如果存在大于2的数,那么最后会非常非常大,不可控,所以构造若干个1相乘
设序列为x -1 2 -1 2…-1 2 y
所以x * y = -x-(n-2) * 2+2 * y
令y=1,则x=-x-2 * n + 4 +2
得2 * x= 6 - 2 * n
得 x =3 - n
由于所有数都不能为0,所以特判一下n为3的情况,直接抄样例
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
int n;
void solve() {cin>>n;if(n==3){cout<<"1 -10 6 6 -10 1"<<endl;return;}cout<<3-n<<' ';for(int i=0;i<(2*n-2)/2;i++){cout<<-1<<' '<<2<<' ';}cout<<1<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) {solve();}return 0;
}
G. Snake Move
题意:
给定n×m地图上的一条长度为k的贪吃蛇。每次操作可以控制贪吃蛇 移动一步或者缩短一格蛇身。对于每个位置,求从初始状态出发最少需要多少次操作使得蛇头到达该处,平方和模 2 64 2^{64} 264
首先分析一下操作,要么蛇头移动一格,身子往前补充原来的位置,蛇尾的位置就空出来了,要么蛇头不动,直接把蛇尾的位置空出来
假设只有蛇头,那么蛇头到任何位置只要跑一个最简单的最短路就可以了,但是由于每次移动只有蛇尾能空出来,所以对于不是蛇身的位置直接跑最短路,而蛇身的位置不能只是简单的最短路,蛇的第i截是在第k-i次之后才空出来,所以我们需要要取max(k-i+1,dist+1)
注意,模 2 64 2^{64} 264就是unsigned int long long
#include<bits/stdc++.h>
#define endl '\n'
//#define int long long
using namespace std;
typedef pair<int,int>PII;
typedef pair<int,PII>PIII;
const int N=3010;
int n,m,k;
int cnt[N][N];
long long dist[N][N];
char s[N][N];
bool vis[N][N];
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
void dijkstra(int a,int b){for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dist[i][j]=1e18;}}dist[a][b]=0;priority_queue<PIII,vector<PIII>,greater<PIII>>heap;heap.push({0,{a,b}});while(heap.size()){auto t=heap.top();heap.pop();int d=t.first,x=t.second.first,y=t.second.second;if(vis[x][y]) continue;vis[x][y]=true;for(int i=0;i<4;i++){int tx=x+dx[i],ty=y+dy[i];if(tx<1||tx>n||ty<1||ty>m) continue;if(vis[tx][ty]||s[tx][ty]=='#') continue;if(dist[tx][ty]>max(d+1,cnt[tx][ty]+1)){dist[tx][ty]=max(d+1,cnt[tx][ty]+1);heap.push({dist[tx][ty],{tx,ty}});}}}
}
void solve() {cin>>n>>m>>k;int sta,stb;for(int i=1;i<=k;i++){int x,y;cin>>x>>y;cnt[x][y]=k-i;if(i==1) sta=x,stb=y;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>s[i][j];}}dijkstra(sta,stb);unsigned int long long ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(dist[i][j]==1e18) continue;ans+=dist[i][j]*dist[i][j];}}cout<<ans<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;
// cin>>t;while(t--) {solve();}return 0;
}
H. Sugar Sweet II
题意:
n 个数a1,a2…an,有 n 个事件,每个事件形如:如果 ai<bi,则 ai = ai +wi,事件随机顺序发生,问每个数的期望
首先,事件是随机发生的,那么肯定和事件发生的顺序有关,我们来分析一下
如果a[i]<a[b[i]],那么事件一定会发生,因为a[b[i]]只能增不能减,所以不管事件的顺序是怎么样的,a[i]始终小于a[b[i]],所以a[i]必定能加上w[i],也就是说a[i]的期望就是a[i]+w[i]
如果a[i]>=a[b[i]]+w[b[i]],那么事件一定不会发生,因为就算先发生a[b[i]]+w[b[i]]这一事件,a[i]也不可能小于a[b[i]],所以a[i]的期望就是a[i]
如果a[b[i]]<=a[i]<a[b[i]]+w[b[i]],那么a[i]+w[i]这一事件发生当且仅当a[b[i]]+w[b[i]]这一事件发生,具有严格的依赖关系
trick:
如果出现严格的依赖关系,可以建图
如果a[i]+w[i]这一事件发生当且仅当a[b[i]]+w[b[i]]这一事件发生,那么连一条边,b[i]->i,建好图之后,当前事件发生当且仅当它前面的事件全部发生并且顺序必须是按照建图的顺序来的,假设它前面有x-1个事件,那么随便排列,只有一种是可以的,概率就是1/x!
所以我们预处理一下深度就可以了
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=5e5+10,mod=1e9+7;
int a[N],b[N],w[N];
int fac[N],ifac[N];
int dist[N];
int n;
int qmi(int a,int b){int res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
vector<vector<int>>e(N);
void dfs(int u){for(auto v:e[u]){dist[v]=dist[u]+1;dfs(v);}
}
void solve() {cin>>n;for(int i=1;i<=n;i++) e[i].clear(),dist[i]=0;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];for(int i=1;i<=n;i++) cin>>w[i];for(int i=1;i<=n;i++){if(a[i]<a[b[i]]) dist[i]=1;else if(a[i]>=a[b[i]]+w[b[i]]) dist[i]=0;else e[b[i]].push_back(i);}for(int i=1;i<=n;i++){if(dist[i]==1){dfs(i);}}for(int i=1;i<=n;i++){if(dist[i]==0) cout<<a[i]<<' ';else if(dist[i]==1) cout<<(a[i]+w[i])%mod<<' ';else cout<<((a[i]+w[i]*ifac[dist[i]])%mod+mod)%mod<<' ';}cout<<endl;
}
signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;//预处理阶乘以及阶乘的逆元fac[0]=ifac[0]=1;//0的阶乘是1,0的阶乘的逆元也是1for(int i=1;i<N;i++) fac[i]=fac[i-1]*i%mod;//预处理阶乘ifac[N-1]=qmi(fac[N-1],mod-2);//先求出fac[N-1]的逆元,由于(n+1)!=n!*(n+1)==>n!^(-1)=(n+1)!^(-1)*(n+1),所以也可以通过递推得到阶乘的逆元for(int i=N-2;i>=1;i--) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;cin>>t;while(t--) {solve();}return 0;
}
相关文章:
)
2023 icpc杭州(M,J,D,G,H)
文章目录 [M. V-Diagram](https://codeforces.com/gym/104976/problem/M)[J. Mysterious Tree](https://codeforces.com/gym/104976/problem/J)[D.Operator Precedence](https://codeforces.com/gym/104976/problem/D)[G. Snake Move](https://codeforces.com/gym/104976/probl…...

在CentOS 7上安装Alist
在CentOS 7上安装Alist 的步骤如下: 1. 卸载旧版本 如果你之前安装过旧版本的Docker,可以先卸载它: sudo yum remove docker docker-common docker-snapshot docker-engine2. 安装依赖包 确保你的系统是最新的,并安装必要的依…...

【C/C++】memcpy函数的模拟实现
零.导言 上一篇博客我们学习了memcpy函数,不妨我们现在尝试模拟实现memcpy函数的功能。 一.实现memcpy函数的要点 memcpy函数是一种C语言内存函数,可以按字节拷贝任意类型的数组,因此我们自定义的模拟函数需要两个无类型的指针参数ÿ…...

嵌入式开发之线程互斥
目录 互斥锁初始化-pthread_mutex_init 申请锁-pthread_mutex_lock 释放锁-pthread_mutex_unlock 同步 VS 互斥 临界资源:一次只允许一个任务(进程、线程)访问的共享资源,不允许多个任务同时访问的。 临界区:访问临界区的代码 互斥机制:mutex互斥锁,任务访问临界资…...

JavaScript 变量作用域与函数调用机制:var 示例详解
JavaScript 变量作用域与函数调用机制:var 示例详解 在 JavaScript 中,作用域和闭包是理解变量生命周期和行为的核心概念。通过以下这段代码,我们将详细分析如何在不同的作用域内使用 var 关键字,并解释相关的变量访问规则 代码解…...
Linux(CentOS)安装 JDK
1、下载 JDK 官网:https://www.oracle.com/ 2、上传 JDK 文件到 CentOS,使用FinalShell远程登录工具,并且使用 root 用户登录 3、解压 JDK 创建目录 /export/server mkdir -p /export/server 解压到目录 /export/server tar -zxvf jdk-17…...

AI产品经理实战手册:策略、开发与商业化指南
通过《AI产品经理手册》,将可以了解不同类型的AI,如何将AI整合到产品或业务中,以及支持创建AI产品或将AI集成到现有产品所需的基础设施。熟悉实践管理AI产品开发流程、评估和优化AI模型,以及应对与AI产品相关的复杂伦理和法律问题…...

【大语言模型】ACL2024论文-06 探索思维链COT在多模态隐喻检测中的应用
【大语言模型】ACL2024论文-06 探索思维链COT在多模态隐喻检测中的应用 目录 文章目录 【大语言模型】ACL2024论文-06 探索思维链COT在多模态隐喻检测中的应用目录摘要研究背景问题与挑战如何解决创新点算法模型1. 知识总结模块(Knowledge Summarization Module&…...

Linux之初体验
目录 第1关:1-Linux初体验 第2关:1-Linux常用命令 第3关:1-Linux 查询命令帮助语句 第4关:2--查询命令-locate 第5关:2--查询命令-which/whereis 第6关:2--查询命令-find 第7关:3-Linux文…...

现代化水电管理:Spring Boot在大学城的实践
2相关技术 2.1 MYSQL数据库 MySQL是一个真正的多用户、多线程SQL数据库服务器。 是基于SQL的客户/服务器模式的关系数据库管理系统,它的有点有有功能强大、使用简单、管理方便、安全可靠性高、运行速度快、多线程、跨平台性、完全网络化、稳定性等,非常…...

黑马官网2024最新前端就业课V8.5笔记---HTML篇
Html 定义 HTML 超文本标记语言——HyperText Markup Language。 标签语法 标签成对出现,中间包裹内容<>里面放英文字母(标签名)结束标签比开始标签多 /拓展 : 双标签:成对出现的标签 单标签:只有开…...
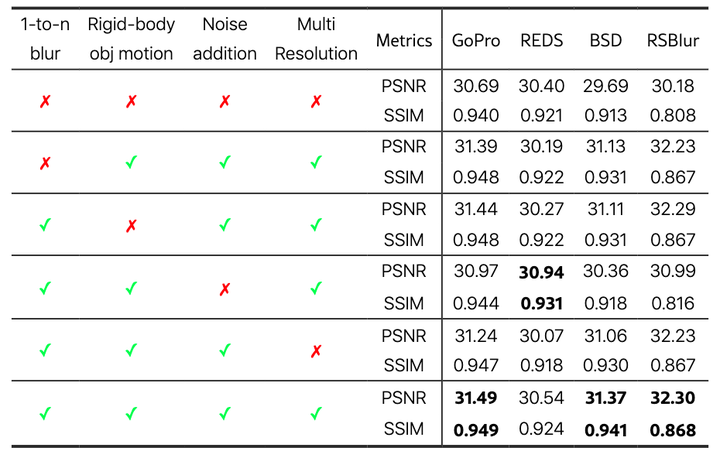
GS-Blur数据集:首个基于3D场景合成的156,209对多样化真实感模糊图像数据集。
2024-10-31,由韩国首尔国立大学的研究团队创建的GS-Blur数据集,通过3D场景重建和相机视角移动合成了多样化的真实感模糊图像,为图像去模糊领域提供了一个大规模、高覆盖度的新工具,显著提升了去模糊算法在真实世界场景中的泛化能力…...

Linux下Java的多种方式安装
Linux下Java的多种方式安装 博客: www.lstar.icu 开源地址 Gitee 地址: https://gitee.com/lxwise/iris-blog_parent Github 地址: https://github.com/lxwise/iris-blog_parent 序言 Java是一门面向对象的编程语言,不仅吸收了…...

Android Studio:connect time out
参考:Android Studio:connect time out_android studio connection timed out-CSDN博客...

A014-基于Spring Boot的家电销售展示平台设计与实现
🙊作者简介:在校研究生,拥有计算机专业的研究生开发团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹 赠送计算机毕业设计600…...

数学期望和联合概率密度
数学期望的定义 数学期望是描述随机变量平均趋势的一个重要统计量。根据随机变量的类型(离散或连续),数学期望的定义有所不同。 离散型随机变量的数学期望: 若离散型随机变量 X X X取值为 x 1 , x 2 , … , x n , … x_1,x_2,\do…...

萤石私有化设备视频平台EasyCVR视频融合平台如何构建农业综合监控监管系统?
现代农业的迅速发展中,集成监控管理系统已成为提高农业生产效率和优化管理的关键工具。萤石私有化设备视频平台EasyCVR,作为一个具有高度可扩展性、灵活的视频处理能力和便捷的部署方式的视频监控解决方案,为农业监控系统的建设提供了坚实的技…...

【MongoDB】Windows/Docker 下载安装,MongoDB Compass的基本使用、NoSQL、MongoDB的基础概念及基础用法(超详细)
文章目录 Windows下载MongoDB Compass使用NoSQL的基本概念MongoDB常用术语MongoDB与RDBMS区别MongoDB的CRUD 更多相关内容可查看 Docker安装MongoDB可查看:Docker-安装MongoDB Windows下载 官网下载地址:https://www.mongodb.com/try/download/communi…...

微信小程序-自定义导航栏
一.自定义导航栏 1.JSON文件中配置"navigationStyle": “custom” "navigationStyle": "custom"2.给导航栏设置轮播图 <swiper class"custom-swiper" indicator-dots autoplay interval"2000"> <swiper-item>…...

vue中强制更新视图
vue3 中强制更新视图 方式 通过 $forceUpdate 与 vue2 相似 import {getCurrentInstance} from vueconst internalInstance getCurrentInstance() //操作数据后更新视图 internalInstance.ctx.$forceUpdate()通过 key 值改变更新 <compName :key"key" />co…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
