【NOIP提高组】计算系数
【NOIP提高组】计算系数
- C语言实现
- C++实现
- Java实现
- Python实现
| 💐The Begin💐点点关注,收藏不迷路💐 |
给定一个多项式 (ax + by)^k ,请求出多项式展开后 x^n y^m 项的系数。
输入
共一行,包含 5 个整数,分别为 a,b,k,n,m,每两个整数之间用一个空格隔开。
输出
输出共 1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对 10007 取 模后的结果。
样例输入
1 1 3 1 2
样例输出
3
提示
【数据范围】 对于 30%的数据,有 0≤k≤10; 对于 50%的数据,有 a = 1,b = 1; 对于 100%的数据,有 0≤k≤1,000,0≤n, m≤k,且 n + m = k,0≤a,b≤1,000,000。
C语言实现
#include <stdio.h>
#include <stdlib.h>// 定义常量
#define N 1010
#define MOD 10007// 二维数组用于存储组合数
int c[N][N];// 输入参数
int a, b, k, n, m;// 快速幂函数,用于计算a的b次幂对MOD取模的结果
int qmi(int a, int b) {a %= MOD;int res = 1;while (b) {if (b & 1) {res = res * a % MOD;}b >>= 1;a = a * a % MOD;}return res;
}int main() {// 读取输入参数scanf("%d %d %d %d %d", &a, &b, &k, &n, &m);// 预处理组合数for (int i = 0; i <= k; i++) {for (int j = 0; j <= i; j++) {if (j == 0) {c[i][j] = 1;} else {c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;}}}// 根据二项式定理计算并输出结果int coefficient = c[k][n] * qmi(a, n) % MOD * qmi(b, m) % MOD;printf("%d\n", coefficient);return 0;
}
C++实现
#include <iostream>
#include <algorithm>// 定义常量
const int N = 1010;
const int MOD = 10007;// 二维数组用于存储组合数
int c[N][N];// 输入参数
int a, b, k, n, m;// 快速幂函数,用于计算a的b次幂对MOD取模的结果
int qmi(int a, int b) {a %= MOD;int res = 1;while (b) {if (b & 1) {res = res * a % MOD;}b >>= 1;a = a * a % MOD;}return res;
}int main() {// 读取输入参数std::cin >> a >> b >> k >> n >> m;// 预处理组合数for (int i = 0; i <= k; i++) {for (int j = 0; j <= i; j++) {if (j == 0) {c[i][j] = 1;} else {c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;}}}// 根据二项式定理计算并输出结果int coefficient = c[k][n] * qmi(a, n) % MOD * qmi(b, m) % MOD;std::cout << coefficient << std::endl;return 0;
}
Java实现
import java.util.Scanner;public class Main {// 定义常量static final int N = 1010;static final int MOD = 10007;// 二维数组用于存储组合数static int[][] c = new int[N][N];// 输入参数static int a, b, k, n, m;// 快速幂函数,用于计算a的b次幂对MOD取模的结果static int qmi(int a, int b) {a %= MOD;int res = 1;while (b!= 0) {if ((b & 1)!= 0) {res = res * a % MOD;}b >>= 1;a = a * a % MOD;}return res;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);// 读取输入参数a = scanner.nextInt();b = scanner.nextInt();k = scanner.nextInt();n = scanner.nextInt();m = scanner.nextInt();// 预处理组合数for (int i = 0; i <= k; i++) {for (int j = 0; j <= i; j++) {if (j == 0) {c[i][j] = 1;} else {c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;}}}// 根据二项式定理计算并输出结果int coefficient = c[k][n] * qmi(a, n) % MOD * qmi(b, m) % MOD;System.out.println(coefficient);}
}
Python实现
# 定义常量
N = 1010
MOD = 10007# 输入参数
a, b, k, n, m = map(int, input().split())# 二维列表用于存储组合数(初始化为全0)
c = [[0] * (N) for _ in range(N)]# 快速幂函数,用于计算a的b次幂对MOD取模的结果
def qmi(a, b):a %= MODres = 1while b:if b & 1:res = res * a % MODb >>= 1a = a * a % MODreturn res# 预处理组合数
for i in range(k + 1):for j in range(i + 1):if j == 0:c[i][j] = 1else:c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD# 根据二项式定理计算并输出结果
coefficient = c[k][n] * qmi(a, n) % MOD * qmi(b, m) % MOD
print(coefficient)

| 💐The End💐点点关注,收藏不迷路💐 |
相关文章:

【NOIP提高组】计算系数
【NOIP提高组】计算系数 C语言实现C实现Java实现Python实现 💐The Begin💐点点关注,收藏不迷路💐 给定一个多项式 (ax by)^k ,请求出多项式展开后 x^n y^m 项的系数。 输入 共一行,包含 5 个整数&#x…...

IDEA部署AI代写插件
前言 Hello大家好,当下是AI盛行的时代,好多好多东西在AI大模型的趋势下都变得非常的简单。 比如之前想画一幅风景画得先去采风,然后写实什么的,现在你只需描述出你想要的效果AI就能够根据你的描述在几分钟之内画出一幅你想要的风景…...

【阅读记录-章节1】Build a Large Language Model (From Scratch)
目录 1. Understanding large language models1.1 What is an LLM?补充介绍人工智能、机器学习和深度学习的关系机器学习 vs 深度学习传统机器学习 vs 深度学习(以垃圾邮件分类为例) 1.2 Applications of LLMs1.3 Stages of building and using LLMs1.4…...

微服务day08
Elasticsearch 需要安装elasticsearch和Kibana,应为Kibana中有一套控制台可以方便的进行操作。 安装elasticsearch 使用docker命令安装: docker run -d \ --name es \-e "ES_JAVA_OPTS-Xms512m -Xmx512m" \ //设置他的运行内存空间&#x…...

JAVA接入WebScoket行情接口
Java脚好用的库很多,开发效率一点不输Python。如果是日内策略,需要更实时的行情数据,不然策略滑点太大,容易跑偏结果。 之前爬行情网站提供的level1行情接口,实测平均更新延迟达到了6秒,超过10只股票并发请…...

使用Axios函数库进行网络请求的使用指南
目录 前言1. 什么是Axios2. Axios的引入方式2.1 通过CDN直接引入2.2 在模块化项目中引入 3. 使用Axios发送请求3.1 GET请求3.2 POST请求 4. Axios请求方式别名5. 使用Axios创建实例5.1 创建Axios实例5.2 使用实例发送请求 6. 使用async/await简化异步请求6.1 获取所有文章数据6…...

Vue2+ElementUI:用计算属性实现搜索框功能
前言: 本文代码使用vue2element UI。 输入框搜索的功能,可以在前端通过计算属性过滤实现,也可以调用后端写好的接口。本文介绍的是通过计算属性对表格数据实时过滤,后附完整代码,代码中提供的是死数据,可…...

抖音热门素材去哪找?优质抖音视频素材网站推荐!
是不是和我一样,刷抖音刷到停不下来?越来越多的朋友希望在抖音上创作出爆款视频,但苦于没有好素材。今天就来推荐几个超级实用的抖音视频素材网站,让你的视频内容立刻变得高大上!这篇满是干货,直接上重点&a…...

spring-cache concurrentHashMap 自定义过期时间
1.自定义实现缓存构建工厂 import java.util.concurrent.ConcurrentHashMap; import java.util.concurrent.ConcurrentMap;import lombok.Getter; import lombok.Setter; import org.springframework.beans.factory.BeanNameAware; import org.springframework.beans.factory.…...

解析传统及深度学习目标检测方法的原理与具体应用之道
深度学习目标检测算法 常用的深度学习的目标检测算法及其原理和具体应用方法: R-CNN(Region-based Convolutional Neural Networks)系列1: 原理: 候选区域生成:R-CNN 首先使用传统的方法(如 Se…...

shell数组
文章目录 🍊自我介绍🍊shell数组概述🍊Shell数组使用方法数组的定义直接定义单元素定义 元素的获取获取单个元素获取全部元素 获取数组长度获取整个数组长度获取单个元素的长度 操作数组增加删除 关联数组 🍊 你的点赞评论就是对博…...

高斯混合模型回归(Gaussian Mixture Model Regression,GMM回归)
高斯混合模型(GMM)是一种概率模型,它假设数据是由多个高斯分布的混合组成的。在高斯混合回归中,聚类与回归被结合成一个联合模型: 聚类部分 — 使用高斯混合模型进行聚类,识别数据的不同簇。回归部分 — 对…...

【3D Slicer】的小白入门使用指南八
3D Slicer DMRI(Diffusion MRI)-扩散磁共振认识和使用 0、简介 大脑解剖 ● 白质约占大脑的 45% ● 有髓神经纤维(大约10微米轴突直径) 白质探索 朱尔斯约瑟夫德杰林(Jules Joseph Dejerine,《神经中心解剖学》(巴黎,1890-1901):基于髓磷脂染色标本的神经解剖图谱)…...

【流量分析】常见webshell流量分析
免责声明:本文仅作分享! 对于常见的webshell工具,就要知攻善防;后门脚本的执行导致webshell的连接,对于默认的脚本要了解,才能更清晰,更方便应对。 (这里仅针对部分后门代码进行流量…...

基于树莓派的边缘端 AI 目标检测、目标跟踪、姿态估计 视频分析推理 加速方案:Hailo with ultralytics YOLOv8 YOLOv11
文件大纲 加速原理硬件安装软件安装基本设置系统升级docker 方案Demo 测试目标检测姿态估计视频分析参考文献前序树莓派文章hailo加速原理 Hailo 发布的 Raspberry Pi AI kit 加速原理,有几篇文章介绍的不错 https://ubuntu.com/blog/hackers-guide-to-the-raspberry-pi-ai-ki…...

Java在算法竞赛中的常用方法
在算法竞赛中,Java以其强大的标准库和高效的性能成为了众多参赛者的首选语言。本文将详细介绍Java在算法竞赛中的常用集合、字符串处理、进制转换、大数处理以及StringBuilder的使用技巧,帮助你在竞赛中更加得心应手。 常用集合 Java的集合框架提供了多…...
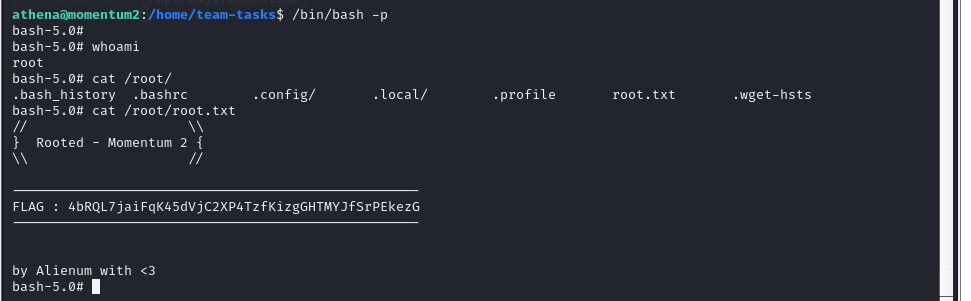
Vulnhub靶场案例渗透[10]- Momentum2
文章目录 一、靶场搭建1. 靶场描述2. 下载靶机环境3. 靶场搭建 二、渗透靶场1. 确定靶机IP2. 探测靶场开放端口及对应服务3. 扫描网络目录结构4. 代码审计5. 反弹shell6. 提权 一、靶场搭建 1. 靶场描述 - Difficulty : medium - Keywords : curl, bash, code reviewThis wor…...

Spark RDD中常用聚合算子源码层面的对比分析
在 Spark RDD 中,groupByKey、reduceByKey、foldByKey 和 aggregateByKey 是常用的聚合算子,适用于按键进行数据分组和聚合。它们的实现方式各不相同,涉及底层调用的函数也有区别。以下是对这些算子在源码层面的分析,以及每个算子…...

计算机网络 (6)物理层的基本概念
前言 计算机网络物理层是OSI模型(开放式系统互联模型)中的第一层,也是七层中的最底层,它涉及到计算机网络中数据的物理传输。 一、物理层的主要任务和功能 物理层的主要任务是处理物理传输介质上的原始比特流,确保数据…...
)
快速上手:Docker 安装详细教程(适用于 Windows、macOS、Linux)
### 快速上手:Docker 安装详细教程(适用于 Windows、macOS、Linux) --- Docker 是一款开源容器化平台,广泛应用于开发、测试和部署。本文将为您提供分步骤的 Docker 安装教程,涵盖 Windows、macOS 和 Linux 系统。 …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
