Leetcode 寻找峰值

为了实现时间复杂度为 O ( log n ) O(\log n) O(logn),可以使用二分查找法:
解题思路:
- 峰值的特性是:当前元素大于左右相邻元素。
- 使用二分法:
- 如果
nums[mid] > nums[mid + 1],说明峰值在左侧或当前mid位置(包括mid),因此将right = mid。 - 否则峰值在右侧,因此将
left = mid + 1。
- 如果
- 不断收缩区间,直到
left == right,此时即找到峰值。
时间复杂度:
- 时间复杂度:(O(\log n)),因为每次迭代都将搜索范围减半。
- 空间复杂度:(O(1)),不需要额外的空间。
java 实现
class Solution {public int findPeakElement(int[] nums) {int left = 0, right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;// 如果中点比右侧元素大,说明峰值在左侧(包括mid)if (nums[mid] > nums[mid + 1]) {right = mid;} else { // 否则峰值在右侧left = mid + 1;}}// 最终left和right会相遇,此时即为峰值位置return left;}
}
数组即便不是有序的,为什么仍然二分查找仍然可以找到峰值?
这是因为这道题的二分查找并不依赖于数组是否有序,而是利用了“峰值”的定义和数组的局部特性。
关键点
-
题目定义的峰值条件:
- 峰值是指某个元素严格大于其左右邻居的元素。
- 如果一个元素
nums[mid] > nums[mid + 1],那么在mid或者其左侧一定存在一个峰值。 - 如果
nums[mid] < nums[mid + 1],那么在mid的右侧一定存在一个峰值。
-
为什么可以二分?
二分查找的核心在于:- 每次选择一个中间点
mid,并根据某个条件判断下一个搜索范围。 - 在这道题中,“峰值”可以通过比较
nums[mid]和nums[mid + 1]来判断范围:- 如果
nums[mid] > nums[mid + 1]:- 峰值在左侧或就是
mid,因为mid本身比右边的大(局部性质),可以舍弃右侧部分。
- 峰值在左侧或就是
- 如果
nums[mid] < nums[mid + 1]:- 峰值一定在右侧,因为右边存在一个更大的值,最终会到达一个下降点形成峰值。
- 如果
这利用了“递增到下降”的局部特性来缩小搜索范围。
- 每次选择一个中间点
-
数学直观解释:
- 假设数组中不存在连续相等的数字(即没有平缓区域),并且在数组两端可以假想有值为负无穷的元素(题目已假设
nums[-1] = nums[n] = -∞)。 - 在数组中总能找到一个峰值元素,原因是:
- 如果数组中存在一个“上升”趋势,例如
nums[i] < nums[i+1],那么在右侧一定有一个峰值。 - 如果数组中存在一个“下降”趋势,例如
nums[i] > nums[i+1],那么左侧也一定存在一个峰值。
- 如果数组中存在一个“上升”趋势,例如
这种趋势保证了每次二分缩小范围后,最终一定会收敛到某个峰值点。
- 假设数组中不存在连续相等的数字(即没有平缓区域),并且在数组两端可以假想有值为负无穷的元素(题目已假设
-
非有序数组的适用性:
题目并没有要求数组有序。因为峰值是局部性质(仅与相邻元素有关),只需要每次确定搜索方向,而不是依赖整体有序性。二分查找法的效率仍然得以保证。
举例说明
以数组 nums = [1, 2, 1, 3, 5, 6, 4] 为例:
- 初始:
left = 0, right = 6,取中间点mid = 3,nums[mid] = 3。- 比较
nums[mid]和nums[mid + 1],3 < 5,说明右侧有峰值,更新left = mid + 1。
- 第二轮:
left = 4, right = 6,取中间点mid = 5,nums[mid] = 6。- 比较
nums[mid]和nums[mid + 1],6 > 4,说明左侧有峰值,更新right = mid。
- 第三轮:
left = 4, right = 5,取中间点mid = 4,nums[mid] = 5。- 比较
nums[mid]和nums[mid + 1],5 < 6,说明右侧有峰值,更新left = mid + 1。
- 最终:
left = right = 5,返回5,此时峰值为6。
总结
二分查找法在这道题中能用,是因为:
- 峰值的定义是局部性质,不依赖数组整体有序性。
- 每次比较中点和其右侧元素,可以有效缩小搜索范围。
- 这种方法本质上是利用数组的递增和递减趋势来确定峰值位置。
相关文章:

Leetcode 寻找峰值
为了实现时间复杂度为 O ( log n ) O(\log n) O(logn),可以使用二分查找法: 解题思路: 峰值的特性是:当前元素大于左右相邻元素。使用二分法: 如果 nums[mid] > nums[mid 1],说明峰值在左侧或当前…...
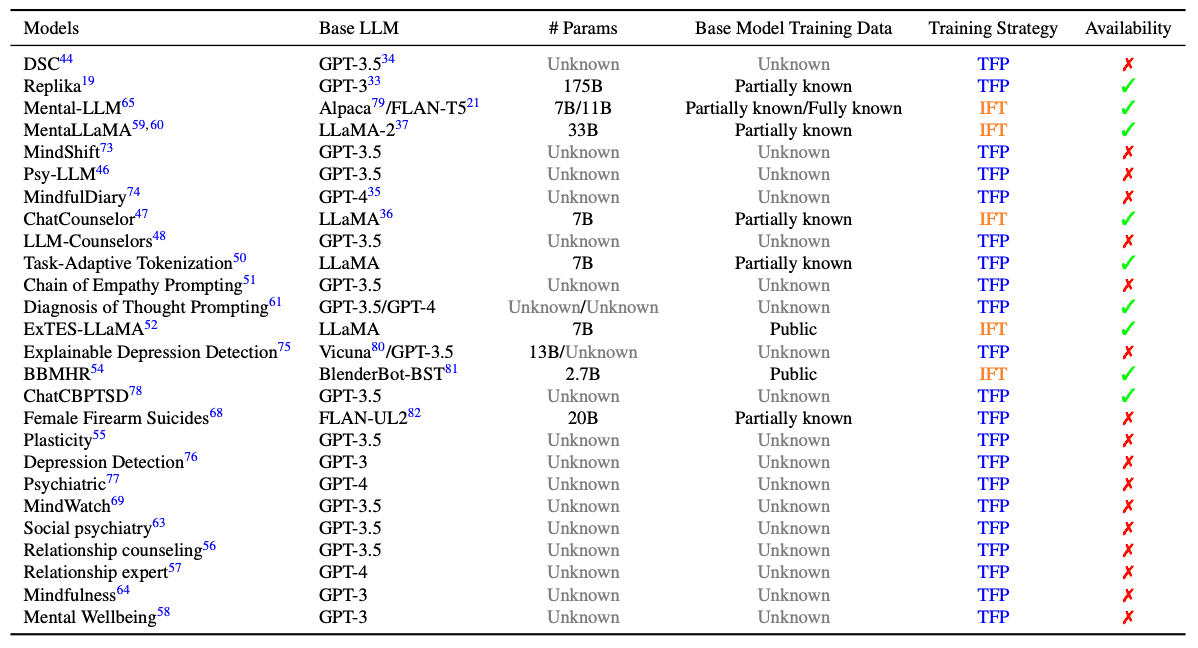
探索大规模语言模型(LLM)在心理健康护理领域中的应用与潜力
概述 心理健康是公共卫生最重要的领域之一。根据美国国家精神卫生研究所(NIMH)的数据,到 2021 年,22.8% 的美国成年人将患上某种形式的精神疾病。在全球范围内,精神疾病占非致命性疾病负担的 30%,并被世界…...

Infisical开源密钥管理平台实战指南
1. 引言 在现代软件开发中,安全地管理环境变量和敏感信息已成为一个关键挑战。Infisical作为一个开源的密钥管理平台,为这一问题提供了强大而灵活的解决方案。本指南将深入探讨Infisical的功能,并通过实际操作步骤,帮助读者全面了解和使用这个工具。 2. Infisical概述 I…...

AI大模型:重塑软件开发流程与模式
人工智能技术的飞速发展,尤其是AI大模型的兴起,正以前所未有的速度和深度影响着各行各业,其中软件开发领域尤为显著。AI大模型,如GPT系列、BERT、Claude等通过其强大的自然语言处理能力、代码理解和生成能力,正在从根本…...

AMD(Xilinx) FPGA配置Flash大小选择
目录 1 FPGA配置Flash大小的决定因素2 为什么选择的Flash容量大小为最小保证能够完成整个FPGA的配置呢? 1 FPGA配置Flash大小的决定因素 在进行FPGA硬件设计时,选择合适的配置Flash是我们进行硬件设计必须考虑的,那么配置Flash大小的选择由什…...
基于Java Springboot图书借阅系统
一、作品包含 源码数据库设计文档万字PPT全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA/eclipse 数据…...

DDRPHY数字IC后端设计实现系列专题之数字后端floorplanpowerplan设计
3.2.3 特殊单元的布局 布图阶段除了布置 I/O 单元和宏单元,在 28nm 制程工艺时,还需要处理两种特 殊的物理单元,Endcap 和 Tapcell。 DDRPHY数字IC后端设计实现系列专题之后端设计导入,IO Ring设计 (1)拐…...

【Mysql】Mysql函数(上)
1、概述 在Mysql中,为了提高代码重用性和隐藏实现细节,Mysql提供了很多函数。函数可以理解为封装好的模块代码。 2、分类 在Mysql中,函数非常多,主要可以分为以下几类: (1)聚合函数 …...

Java连接MySQL(测试build path功能)
Java连接MySQL(测试build path功能) 实验说明下载MySQL的驱动jar包连接测试的Java代码 实验说明 要测试该情况,需要先安装好MySQL的环境,其实也可以通过测试最后提示的输出来判断build path是否成功,因为如果不成功会直…...

卡尔曼滤波器
卡尔曼滤波器概述 卡尔曼滤波器(Kalman Filter)是一种递归的最优估计方法,广泛应用于信号处理、控制理论、导航定位等领域。它基于线性动态系统模型,通过观测数据不断更新系统的状态估计,从而使得估计值能够在噪声干扰…...

基于BERT的情感分析
基于BERT的情感分析 1. 项目背景 情感分析(Sentiment Analysis)是自然语言处理的重要应用之一,用于判断文本的情感倾向,如正面、负面或中性。随着深度学习的发展,预训练语言模型如BERT在各种自然语言处理任务中取得了…...

推荐15个2024最新精选wordpress模板
以下是推荐的15个2024年最新精选WordPress模板,轻量级且SEO优化良好,适合需要高性能网站的用户。中文wordpress模板适合搭建企业官网使用。英文wordpress模板,适合B2C网站搭建,功能强大且兼容性好,是许多专业外贸网站的…...

AWTK-WIDGET-WEB-VIEW 实现笔记 (2) - Windows
在 Windows 平台上的实现,相对比较顺利,将一个窗口嵌入到另外一个窗口是比较容易的事情。 1. 创建窗口 这里有点需要注意: 父窗口的大小变化时,子窗口也要跟着变化,否则 webview 显示不出来。创建时窗口的大小先设置…...

Linux四剑客及正则表达式
正则表达式 基础正则(使用四剑客命令时无需加任何参数即可使用) ^ # 匹配以某一内容开头 如:^grep匹配所有以grep开头的行。 $ # 匹配以某一内容结尾 如:grep$ 匹配所有以grep结尾的行。 ^$ # 匹配空行。 . # 匹配…...
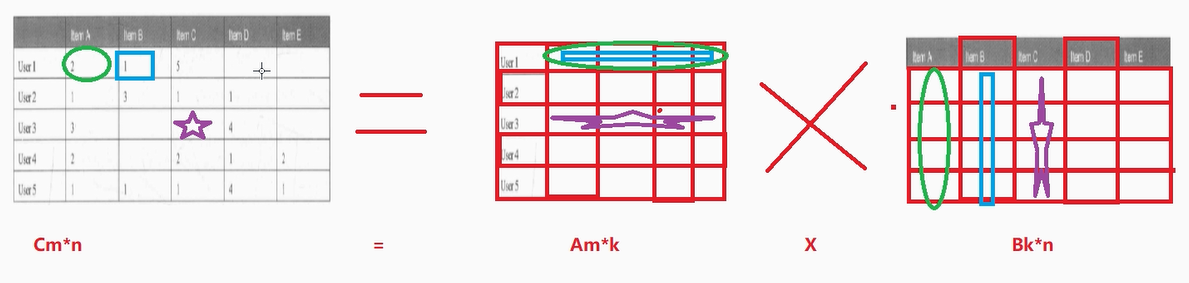
ALS 推荐算法案例演示(python)
数学知识补充:矩阵 总结来说: Am*k X Bk*n Cm*n ----至于乘法的规则,是数学问题, 知道可以乘即可,不需要我们自己计算 反过来 Cm*n Am*k X Bk*n ----至于矩阵如何拆分/如何分解,是数学问题,知道可以拆/可以分解即可 ALS 推荐算法案例:电影推…...

labview中连接sql server数据库查询语句
当使用数据库查询功能时,我们需要用到数据库的查询语句,这里已调用sql server为例,我们需要按照时间来查询,这里在正常调用数据库查询语句时,我们需要在前面给他加一个限制条件这里用到了,数据库的查询语句…...

leetcode_二叉树最大深度
对二叉树的理解 对递归调用的理解 对内存分配的理解 基础数据结构(C版本) - 飞书云文档 每次函数的调用 都会进行一次新的栈内存分配 所以lmax和rmax的值不会混在一起 /*** Definition for a binary tree node.* struct TreeNode {* int val;* …...

Elasticsearch 重建索引 数据迁移
Elasticsearch 重建索引 数据迁移 处理流程创建临时索引数据迁移重建索引写在最后 大家都知道,es的索引创建完成之后就不可以再修改了,包括你想更改字段属性或者是分词方式等。那么随着业务数据量的发展,可能会出现需要修改索引,或…...

2411rust,异步函数
原文 Rust异步工作组很高兴地宣布,在实现在特征中使用异步 fn的目标方面取得了重大进度.将在下周发布稳定的Rust1.75版,会包括特征中支持impl Trait注解和async fn. 稳定化 自从RFC#1522在Rust1.26中稳定下来以来,Rust就允许用户按函数的返回类型(一般叫"RPIT")编…...

前端网络性能优化问题
DNS预解析 DNS 解析也是需要时间的,可以通过预解析的⽅式来预先获得域名所对应的 IP。 <link rel"dns-prefetch" href"//abcd.cn"> 缓存 强缓存 在缓存期间不需要请求, state code 为 200 可以通过两种响应头实现&#…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
