泛微E9与金蝶云星空的集成方案:实现审批流程与财务管理的无缝对接
泛微E9与金蝶云星空的集成方案:实现审批流程与财务管理的无缝对接
背景介绍:
在企业日常运营中,泛微OA-E9和金蝶云星空是两个关键的系统。泛微OA-E9是一款广受企业青睐的办公自动化软件,它通过流程管理、文档管理、协同办公等模块,助力企业提升办公效率。金蝶云星空则以其灵活的业务架构和财务管理功能,支持企业的运营管理和财务统一化管理。

集成目标:
通过泛微OA-E9发起的审批流程,将审批结果和意见自动回传至金蝶云星空,实现内部办公与财务管理的一体化,特别是在报销申请和付款申请等场景中。
集成步骤:
- 系统连接:
确保泛微E9和金蝶云星空之间的数据传输和通信。这需要获取并配置两个系统的连接参数,并进行基础测试以确保连接性。
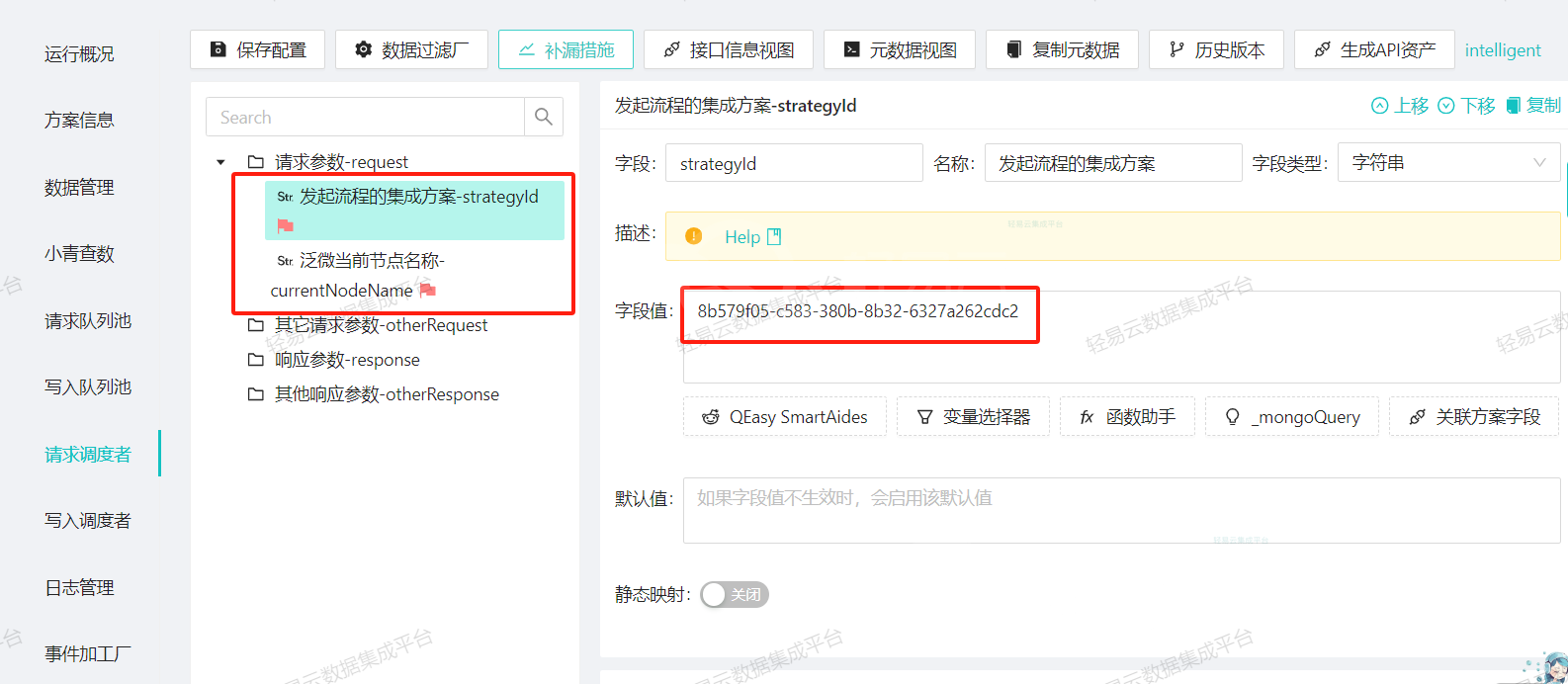
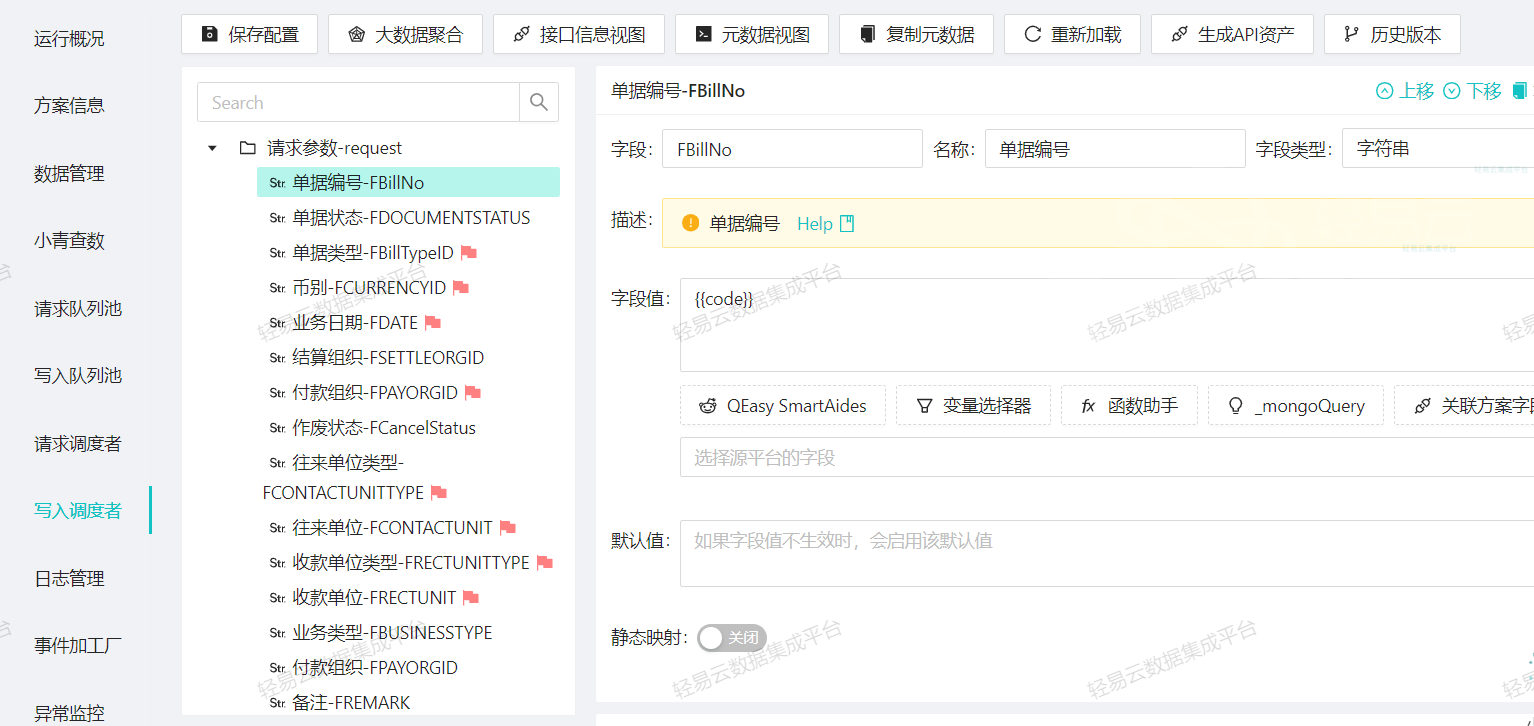
- 数据映射与转换规则:
根据企业需求,定义金蝶与泛微E9之间的数据对接规则。这包括确定数据传输的方向、生成的财务单据类型、数据逻辑处理、审批意见和附件的传输等,以确保集成后的单据符合管理要求。- 泛微查询流程接口配置: 需要配置发起流程的表单ID、流程节点以及返回参数。
- 参数映射关系处理: 配置写入参数,确保数据准确映射。
-
定时执行方案:
在泛微OA系统中,用户可以通过以下步骤设置定时执行方案:-
选择方案: 从可用方案列表中选择需要定时执行的方案。
-
设置时间和频率: 指定执行的具体日期和时间,或设定循环周期及执行次数。
-
配置其他参数: 如接收人、附件、执行条件等。
-
启用定时任务: 完成设置后启用定时任务,确保方案按计划自动执行。
定时执行方案有助于减少手动操作,提高工作效率和准确性,确保业务活动按时进行。
-
集成成果:
泛微OA-E9与金蝶云星空的集成实现了业务单据的自动同步、客户和供应商数据的实时更新、多层级部门数据的精确处理、审批结果和意见的及时回传,以及合同和报销审批流程的无缝对接,从而提升了企业的决策效率,降低了运营成本,并优化了资源配置,实现了内部办公与财务管理的一体化,增强了企业的整体管理效能。
系统集成过程中可能会遇到字段解析、表单流程处理、数据写入格式逻辑转化等技术难点。如需深入了解这些挑战,欢迎随时联系我们。

相关文章:

泛微E9与金蝶云星空的集成方案:实现审批流程与财务管理的无缝对接
泛微E9与金蝶云星空的集成方案:实现审批流程与财务管理的无缝对接 背景介绍: 在企业日常运营中,泛微OA-E9和金蝶云星空是两个关键的系统。泛微OA-E9是一款广受企业青睐的办公自动化软件,它通过流程管理、文档管理、协同办公等模…...

理解设计模式与 UML 类图:构建稳健软件架构的基石
在软件开发的广阔天地里,设计模式与 UML(统一建模语言)类图犹如两座灯塔,为开发者照亮前行的道路,指引着我们构建出高质量、可维护且易于扩展的软件系统。今天,就让我们一同深入探索单一职责、开闭原则、简…...

FastAPI重载不生效?解决PyCharm中Uvicorn无法重载/重载缓慢的终极方法!
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 重载缓慢 📒📝 问题概述🚨 相关原因📝 解决方案一📝 解决方案二📝 解决方案三📝 解决方案四⚓️ 相关链接 ⚓️📖 介绍 📖 在使用FastAPI开发时,reload=True 本应让你在修改代码后自动重启服务,提升开发效率…...
最新子比主题zibll8.0开心版源码 无加密无后门
Zibll子比主题专为博客、自媒体及资讯类网站精心打造,以其简约而不失高雅的设计风格,为网站增添独特魅力与视觉美感。 8.0更新内容: 新增发帖选择板块、话题、标签时支持搜索,同时优化了选择栏目,更加方便快捷 新增小工具文章列表…...

【数据分析】认清、明确
1、什么是数据分析。 - 通过对大量的数据进行科学的分析。 - 得出结论,提出建议,辅助公司企业的决策。2、数据分析分为几步。 - 1.明确目的! - 2.收集数据!自己的数据! 自动化采集的数据! - 3.数据处理! - 4.数据分析!数据分析(业务)数据挖掘(代码算法…...

工业生产安全-安全帽第二篇-用java语言看看opencv实现的目标检测使用过程
一.背景 公司是非煤采矿业,核心业务是采选,大型设备多,安全风险因素多。当下政府重视安全,头部技术企业的安全解决方案先进但价格不低,作为民营企业对安全投入的成本很敏感。利用我本身所学,准备搭建公司的…...

人工智能(AI)与机器学习(ML)基础知识
目录 1. 人工智能与机器学习的核心概念 什么是人工智能(AI)? 什么是机器学习(ML)? 什么是深度学习(DL)? 2. 机器学习的三大类型 (1)监督式学…...
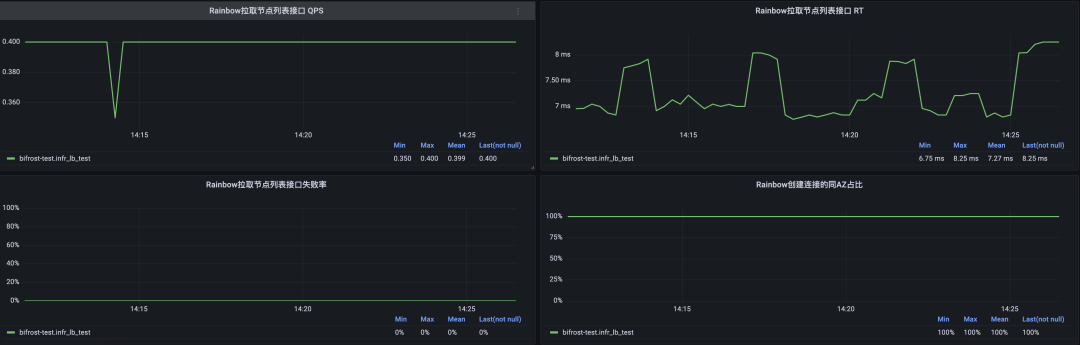
得物彩虹桥架构演进之路-负载均衡篇
文 / 新一 一、前言 一年一更的彩虹桥系列又来了,在前面两期我们分享了在稳定性和性能2个层面的一些演进&优化思路。近期我们针对彩虹桥 Proxy 负载均衡层面的架构做了一次升级,目前新架构已经部署完成,生产环境正在逐步升级中…...
Jmeter中的断言(四)
13--XPath断言 功能特点 数据验证:验证 XML 响应数据是否包含或不包含特定的字段或值。支持 XPath 表达式:使用 XPath 表达式定位和验证 XML 数据中的字段。灵活配置:可以设置多个断言条件,满足复杂的测试需求。 配置步骤 添加…...
)
vue2 src_Todolist编辑($nextTick)
main.js //引入Vue import Vue from "vue"; //引入App import App from ./App;//关闭Vue的生产提示 Vue.config.productionTip false;new Vue({el: #app,render: h > h(App),beforeCreate() {//事件总线Vue.prototype.$bus this;} });App.vue <template>…...

driver.js实现页面操作指引
概述 在访问某些网站的时候,第一次进去你会发现有个操作指引,本文引用driver.js,教你在你的页面也加入这般高大上的操作指引。 实现效果 实现 driver.js简介 driver.js是一个功能强大且高度可定制的基于原生JavaScript开发的新用户引导库…...

ffmpeg区域颜色覆盖
ffmpeg去除水印(遮盖指定区域)的几种办法_ffmpeg去水印-CSDN博客 ffmpeg -i a.mp4 -vf "drawboxx1560:y30:w310:h100:tfill" b.mp4 drawbox在视频帧上绘制一个矩形: x和y:矩形左上角的坐标。默认值是0。 w和h:矩形的宽度和高度。…...

【Python TensorFlow】进阶指南(续篇三)
在前几篇文章中,我们探讨了TensorFlow的高级功能,包括模型优化、分布式训练、模型解释等多个方面。本文将进一步深入探讨一些更具体和实用的主题,如模型持续优化的具体方法、异步训练的实际应用、在线学习的实现细节、模型服务化的最佳实践、…...

QT 实现仿制 网络调试器(未实现连接唯一性) QT5.12.3环境 C++实现
网络调试助手: 提前准备:在编写代码前,要在.pro工程文件中,添加network模块。 服务端: 代码: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QtWidgets> #inclu…...

【英特尔IA-32架构软件开发者开发手册第3卷:系统编程指南】2001年版翻译,2-31
文件下载与邀请翻译者 学习英特尔开发手册,最好手里这个手册文件。原版是PDF文件。点击下方链接了解下载方法。 讲解下载英特尔开发手册的文章 翻译英特尔开发手册,会是一件耗时费力的工作。如果有愿意和我一起来做这件事的,那么ÿ…...

面试题---深入源码理解MQ长轮询优化机制
引言 在分布式系统中,消息队列(MQ)作为一种重要的中间件,广泛应用于解耦、异步处理、流量削峰等场景。其中,延时消息和定时消息作为MQ的高级功能,能够进一步满足复杂的业务需求。为了实现这些功能…...

stable diffusion生成模型
1、stable diffusion Stable Diffusion 是一种扩散模型,基于对图像的逐步去噪过程训练和生成。它的核心包括以下几个步骤: 扩散过程(Diffusion Process)在训练时,向真实图像逐步添加噪声,最终将其变为纯随机噪声。这是一个正向过程,目的是学习如何将复杂的图像分解成随…...

分治法的魅力:高效解决复杂问题的利器
文章目录 分治法 (Divide and Conquer) 综合解析一、基本原理二、应用场景及详细分析1. 排序算法快速排序 (Quicksort)归并排序 (Mergesort) 2. 大整数运算大整数乘法 3. 几何问题最近点对问题 4. 字符串匹配KMP算法的优化版 三、优点四、局限性五、分治法与动态规划的对比六、…...

Spring IOC实战指南:从零到一的构建过程
Spring 优点: 方便解耦,简化开发。将所有对象创建和依赖关系维护交给 Spring 管理(IOC 的作用)AOP 切面编程的支持。方便的实现对程序进行权限的拦截、运行监控等功能(可扩展性)声明式事务的支持。只需通过配置就可以完成对事务的管理,无需手…...
)
3.langchain中的prompt模板 (few shot examples in chat models)
本教程将介绍如何使用LangChain库和智谱清言的 GLM-4-Plus 模型来理解和推理一个自定义的运算符(例如使用鹦鹉表情符号🦜)。我们将通过一系列示例来训练模型,使其能够理解和推断该运算符的含义。 环境准备 首先,确保…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
