Python操作neo4j库py2neo使用(一)
Python操作neo4j库py2neo使用(一)
安装(只用于测试)
docker-compose .yml 文件
version: '3.8'
services:neo4j:image: neo4j:5.6.0-enterprise #商业版镜像hostname: neo4jcontainer_name: neo4jports:- "7474:7474"- "7687:7687"volumes:- ./neo4j/data:/data- ./neo4j/logs:/logs- ./neo4j/conf:/var/lib/neo4j/conf- ./neo4j/import:/var/lib/neo4j/importenvironment:NEO4J_AUTH: neo4j/neo4j@123 # 登录的账号密码NEO4J_ACCEPT_LICENSE_AGREEMENT: yes # 开启商业版license
启动方式
在 docker-compose .yml 文件的同目录下
docker-compose up -d
py2neo连接及创建数据库
1、安装
pip install py2neo
2、连接数据库
# 连接指定数据库,name为库名,不指定则默认连接neo4j
from py2neo import Graph
graph = Graph("bolt://xx.xx.xx.xx:7687", auth=(user, pwd), name=graph_name)# 连接数据库服务
from py2neo import GraphService
graph_service = GraphService("bolt://xx.xx.xx.xx:7687", auth=(user, pwd))
# 可根据数据库名获取指定的数据
graph = graph_service[graph_name]
3、创建数据库(社区版不支持创建多个数据库,只允许使用默认的neo4j)
# 只有商业版支持多库创建
# 连接数据库服务
from py2neo import GraphService
graph_service = GraphService("bolt://xx.xx.xx.xx:7687", auth=(user, pwd))
# 获取system数据库
graph = graph_service['system']
# 创建指定数据库,注意neo4j的数据库名不支持'-'和'_'
graph.run(f'create database {graph_name}')
相关文章:
)
Python操作neo4j库py2neo使用(一)
Python操作neo4j库py2neo使用(一) 安装(只用于测试) docker-compose .yml 文件 version: 3.8 services:neo4j:image: neo4j:5.6.0-enterprise #商业版镜像hostname: neo4jcontainer_name: neo4jports:- "7474:7474"-…...

Oracle - 多区间按权重取值逻辑 ,分时区-多层级-取配置方案(二)
Oracle - 多区间按权重取值逻辑 ,分时区-多层级-取配置方案https://blog.csdn.net/shijianduan1/article/details/133386281 某业务配置表,按配置的时间区间及组织层级取方案,形成报表展示出所有部门方案的取值; 例如࿰…...

leetcode刷题记录(四十二)——101. 对称二叉树
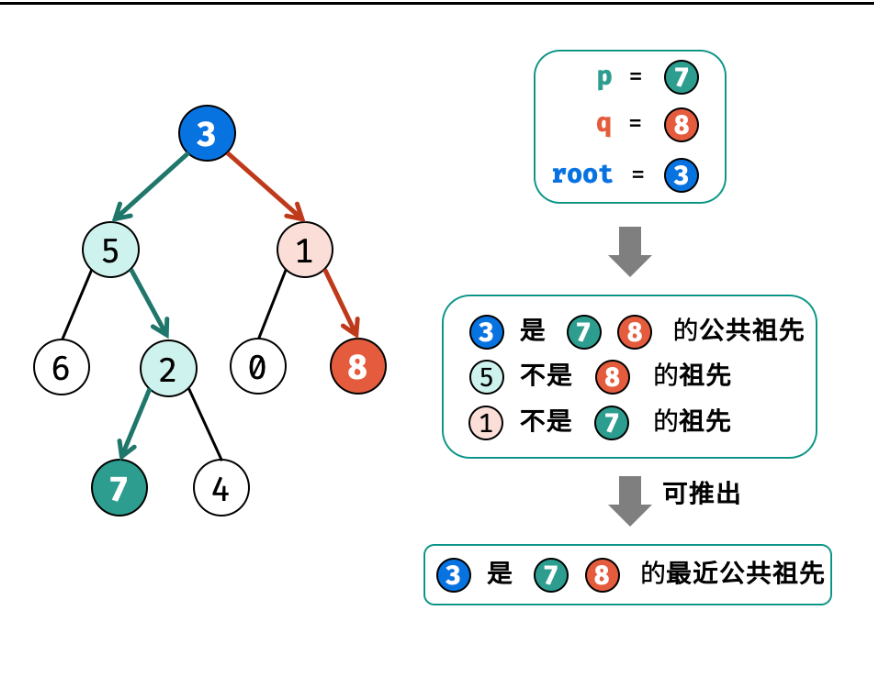
(一)问题描述 . - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。https://leetcode.cn/problems/symmetric-tree/description/给你…...

AutoDL安装docker问题
在AutoDL上租了卡,安装docker遇到一些问题: 1.执行 sudo docker run hello-world 报错 docker: Cannot connect to the Docker daemon at unix:///var/run/docker.sock. Is the docker daemon running? 解决方法 先查看docker有没有启动,…...
)
C++头文件大全(要是还有请帮忙)
以下是 C 中常见的各类头文件分类列举(但实际远不止这些,随着标准库扩充及第三方库使用会有更多): 输入 / 输出流相关头文件 <iostream>:用于标准输入输出,定义了 cin、cout 等对象。<fstream>…...

深度学习实战人脸识别
文章目录 前言一、人脸识别一般过程二、人脸检测主流算法1. MTCNN2. RetinaFace3. CenterFace4. BlazeFace5. YOLO6. SSD7. CascadeCNN 三、人脸识别主流算法1.deepface2.FaceNet3.ArcFace4.VGGFace5.DeepID 四、人脸识别系统实现0.安装教程与资源说明1. 界面采用PyQt5框架2.人…...

oracle排查长时间没提交的事务造成的阻塞案例
一 问题描述 开发同事反馈生产环境某个接口慢,一个普通的按主键更新的update竟然需要5分钟,而我手动执行秒返回,猜测是发生了阻塞,需要排查出阻塞源。 有时,一个事务里会包含多个sql,有的还包含上传附件等…...

React第七节 组件三大属性之 refs 的用法注意事项
1、定义 React 中refs 是允许我们操作DOM 访问组件实例的一种方案。开发人员可以直接使用 refs 访问操作DOM,而不用自身的数据状态,这种方案在实际开发过程中是有必要的,但是不建议通篇使用refs操作DOM,如果是这样,那…...

工程企业需要什么样的物资管理系统?为什么需要物资管理系统?
一、背景与意义 在工程项目的建设中,无论是高楼大厦的拔地而起,还是高速公路的绵延铺展,物资都是最基础的要素之一。从钢筋水泥到施工机械,任何一种物资的管理不善都可能导致项目延误、成本超支,甚至质量问题。然而&a…...

基于网页的大语言模型聊天机器人
代码功能 用户交互界面: 包括聊天历史显示区域和输入框,用户可以输入消息并发送。 消息发送和显示: 用户输入消息后点击“Send”按钮或按下回车键即可发送。 消息发送后显示在聊天记录中,并通过异步请求与后端 AI 模型通信&am…...
)
深入理解索引(一)
1.引言 在数据库和数据结构中,索引(Index)是一种用于提高数据检索速度的重要机制。本文将详细深入介绍索引。 2. 索引的分类 2.1 B - 树索引(B - Tree Index) 2.1.1 结构细节 树状结构:B - 树索引是一…...

动态规划子数组系列一>最长湍流子数组
1.题目: 解析: 代码: public int maxTurbulenceSize(int[] arr) {int n arr.length;int[] f new int[n];int[] g new int[n];for(int i 0; i < n; i)f[i] g[i] 1;int ret 1;for(int i 1; i < n-1; i,m. l.kmddsfsdafsd){int…...

MATLAB矩阵元素的修改及删除
利用等号赋值来进行修改 A ( m , n ) c A(m,n)c A(m,n)c将将矩阵第 m m m行第 n n n列的元素改为 c c c,如果 m m m或 n n n超出原来的行或列,则会自动补充行或列,目标元素改为要求的,其余为 0 0 0 A ( m ) c A(m)c A(m)c将索引…...

对 TypeScript 中函数如何更好的理解及使用?与 JavaScript 函数有哪些区别?
TypeScript 中函数的理解 在 TypeScript 中,函数本质上与 JavaScript 中的函数类似,但是它增强了类型系统的支持,使得我们可以对函数的参数和返回值进行更严格的类型检查。这样可以有效减少类型错误,提高代码的可维护性和可读性。…...

ubuntu搭建k8s环境详细教程
在Ubuntu上搭建Kubernetes(K8s)环境可以通过多种方式实现,下面是一个详细的教程,使用kubeadm工具来搭建Kubernetes集群。这个教程将涵盖从准备工作到安装和配置Kubernetes的所有步骤。 环境准备 操作系统:确保你使用的…...

ubuntu安装Eclipse
版本 ubuntu16.04 64bitEclipse 2019-12 (太高容易崩溃)下载:wget https://archive.eclipse.org/technology/epp/downloads/release/2019-12/R/eclipse-java-2019-12-R-linux-gtk-x86_64.tar.gzjdk安装 将jdk1.8.0_211-linux-x64.tar.gz解压到…...

C#里怎么样使用线程暂停?
C#里怎么样使用线程暂停? 如果一个线程没有任务在处理,并且又不进行暂停, 这时候,这个线程就会把当前这个CPU占满,即是所谓的死循环。 因此我们设计线程时,一定要知道线程在什么时候没有工作处理时, 就需要进入等待状态,不能再进行下去,否则会导致死循环, 只是耗费…...

畅听FM 3.0.0 | 很有果味的电台软件,超多FM电台,支持播放本地音乐
畅听FM是一款简洁且富有设计感的电台软件,支持收听超多FM电台,还支持播放本地音乐,甚至可以用网址创建音乐源。3.0新版本主要改进了对Android 4.x系统的支持,使得老旧电视和车机也能安装使用,并且新增了横屏显示功能&a…...
力扣面试经典 150(上)
文章目录 数组/字符串1. 合并两个有序数组2. 移除元素3. 删除有序数组中的重复项4. 删除有序数组的重复项II5. 多数元素6. 轮转数组7. 买卖股票的最佳时机8. 买卖股票的最佳时机II9. 跳跃游戏10. 跳跃游戏II11. H 指数12. O(1)时间插入、删除和获取随机元素13. 除自身以外数组的…...

鸿蒙开发-音视频
Media Kit 特点 一般场合的音视频处理,可以直接使用系统集成的Video组件,不过外观和功能自定义程度低Media kit:轻量媒体引擎,系统资源占用低支持音视频播放/录制,pipeline灵活拼装,插件化扩展source/demu…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
