Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素

那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。
例如要查询一个名字是否在这所学校里。
要枚举的话时间复杂度是O(n),但如果使用哈希表的话, 只需要O(1)就可以做到。
我们只需要初始化把这所学校里学生的名字都存在哈希表里,在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。
将学生姓名映射到哈希表上就涉及到了hash function ,也就是哈希函数。
242.有效的字母异位词
题目:给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。力扣题目链接
思路:定义一个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历 字符串s的时候,只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数,统计出来了。
那看一下如何检查字符串t中是否出现了这些字符,同样在遍历字符串t的时候,对t中出现的字符映射哈希表索引上的数值再做-1的操作。
那么最后检查一下,record数组如果有的元素不为零0,说明字符串s和t一定是谁多了字符或者谁少了字符,return false。
最后如果record数组所有元素都为零0,说明字符串s和t是字母异位词,return true。
时间复杂度为O(n),空间上因为定义是的一个常量大小的辅助数组,所以空间复杂度为O(1)。
class Solution {
public:bool isAnagram(string s, string t) {int record[26] = {0};for (int i = 0; i < s.size(); i++){record[s[i] - 'a']++;}for (int i = 0; i < t.size(); i++){record[t[i] - 'a']--;}for (int i = 0; i < 26; i++){if(record[i] != 0){return false;}}return true;}
};349. 两个数组的交集
题目:给定两个数组,编写一个函数来计算它们的交集。力扣题目链接
思路:注意题目特意说明:输出结果中的每个元素一定是唯一的,也就是说输出的结果的去重的, 同时可以不考虑输出结果的顺序
std::set和std::multiset底层实现都是红黑树,std::unordered_set的底层实现是哈希表, 使用unordered_set 读写效率是最高的,并不需要对数据进行排序,而且还不要让数据重复,所以选择unordered_set。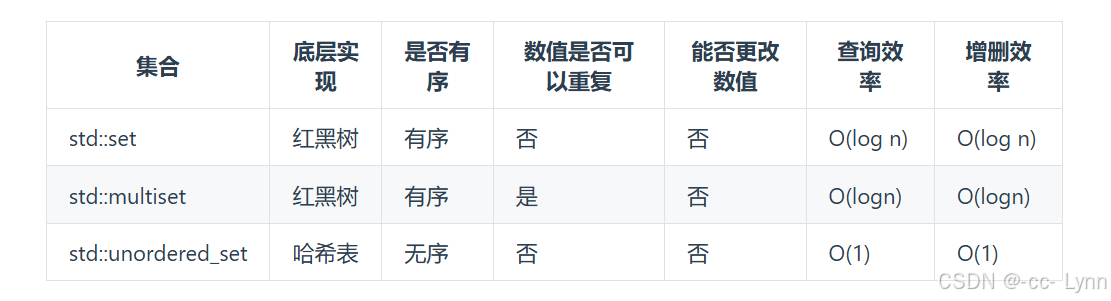
class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> result_set; // 存放结果,之所以用set是为了给结果集去重unordered_set<int> nums_set(nums1.begin(), nums1.end());for (int num : nums2) {// 发现nums2的元素 在nums_set里又出现过if (nums_set.find(num) != nums_set.end()) {result_set.insert(num);}}return vector<int>(result_set.begin(), result_set.end());}
};unordered_set<int> nums_set(nums1.begin(), nums1.end()); 解释:
这行代码将
nums1中的所有元素插入到nums_set中。nums1.begin()和nums1.end()分别是nums1向量的起始迭代器和结束迭代器,表示整个nums1向量的范围。
for (int num : nums2) 解释:
是 C++ 中的一种范围基于的循环(range-based for loop)语法。这种语法用于遍历容器或数组中的每个元素,而无需显式地使用迭代器或索引。它使代码更加简洁和易读。
具体来说,
for (int num : nums2)的含义是:
int num:声明一个变量num,其类型为int。在每次循环迭代中,num会依次取nums2中的每个元素的值。nums2:要遍历的容器或数组。在这个例子中,nums2是一个std::vector<int>类型的向量。因此,
for (int num : nums2)的完整意思是:对于nums2中的每个元素,将该元素的值赋给num,然后执行循环体内的代码。
在 C++ 中,
unordered_set(以及set、map等关联容器)提供了一个成员函数find,用于查找容器中是否存在某个特定的键。find函数的返回值是一个迭代器,指向找到的元素;如果未找到该元素,则返回一个特殊的迭代器,通常称为“结束迭代器”(end iterator),即end()。
第202题. 快乐数
题目:
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
思路:题目中说了会 无限循环,那么也就是说求和的过程中,sum会重复出现,这对解题很重要!【对哈希表的算法我也不大会,只能说是多积累吧】
class Solution {
public:int getSum(int n) {int sum = 0;while(n){sum += (n % 10) * (n % 10);n /= 10;}return sum;}bool isHappy(int n) {unordered_set<int> set;while(1){int sum = getSum(n);if(sum == 1){return true;}if(set.find(sum) != set.end()){return false;}else{set.insert(sum);}n = sum;}}
};相关文章:

Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。 例如要查询一个名字是否在这所学校里。 要枚举的话时间复杂度是O(n),但如果使用哈希…...
windows实现VNC连接ubuntu22.04服务器
最近弄了一个700块钱的mini主机,刷了ubuntu22.04系统,然后想要在笔记本上通过VNC连接,这样就有了一个linux的开发环境。最后实现的过程为: 安装vnc服务器 安装 VNC 服务器软件: sudo apt update sudo apt install t…...

中国电信星辰大模型:软件工厂与文生视频技术的深度解析
在科技日新月异的今天,人工智能(AI)技术正以惊人的速度改变着我们的生活和工作方式。作为这一领域的领军企业之一,中国电信凭借其强大的研发实力和深厚的技术积累,推出了星辰大模型,旨在为用户带来更加智能、高效、便捷的服务体验。本文将重点介绍中国电信星辰大模型中的…...

项目实战:基于Vue3实现一个小相册
相册的示例效果图 注意看注释... 要实现图片的相册效果,图片命名可以像{img1.jpg,img2.jpg,img3.jpg}类似于这种的命名方式。 CSS部分: <style>/* 伪元素选择器,用于在具有clear_ele类的元素内部的末尾添加一个新的元素 */.clear_ele:…...

macOS安装nvm node
macOS安装nvm macOS安装nvm创建 nvm 工作目录配置环境变量使用 nvm查看可用的 Node.js 版本安装特定版本 macOS安装nvm brew install nvm创建 nvm 工作目录 mkdir ~/.nvm配置环境变量 vim ~/.zshrc# nvm export NVM_DIR"$HOME/.nvm" [ -s "/opt/homebrew/opt…...

解决整合Django与Jinja2兼容性的问题
提问 解决整合Django与Jinja2时遇到了一些兼容性问题。已经按照常规步骤在我的settings.py中配置了Jinja2作为模板引擎,同时保留了Django默认的模板设置。然而尝试同时使用Django和Jinja2时,系统报错提示我没有指定模板。如果我尝试移除Django的默认模板…...

Elasticsearch面试内容整理-高级特性
Elasticsearch 提供了一系列高级特性,这些特性可以极大地增强其搜索、分析和管理能力,使得它在大数据场景中表现出色。以下是 Elasticsearch 的一些重要高级特性: 近实时搜索(Near Real-Time Search) Elasticsearch 的一个关键特性是 近实时搜索(NRT),这意味着数据写入…...

linux通过手工删除文件卸载oracle 11g rac的具体步骤
在linux操作系统中,有些时候我们自己学习和测试会临时搭建的oracle rac。事情完成后,我们想回收资源,需要去卸载oracle rac。为了快速卸载oracle rac,今天我们介绍下如何通过手工删除文件的方式来完成工作(操作都需要在…...
【ArcGISPro】根据yaml构建原始Pro的conda环境
使用场景 我们不小心把原始arcgispro-py3的conda环境破坏了,我们就可以使用以下方法进行修复 查找文件 在arcgis目录下找到yaml文件 如果没找到请复制以下内容到新的yaml文件 channels: - esri - defaults dependencies: - anyio=4.2.0=py311haa95532_0 - appdirs=1.4.4=p…...
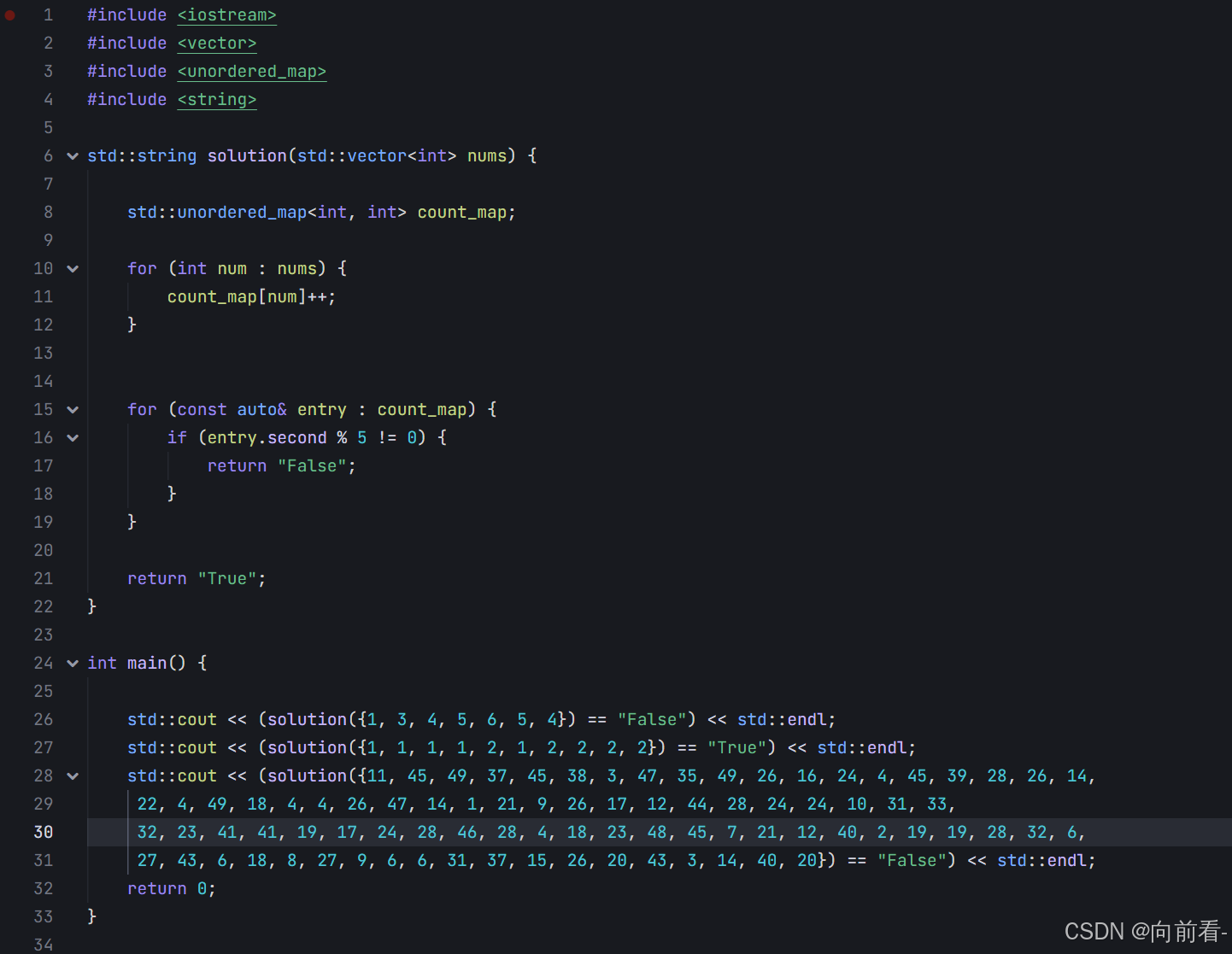
刷题笔记15
问题描述 小M和小F在玩飞行棋。游戏结束后,他们需要将桌上的飞行棋棋子分组整理好。现在有 N 个棋子,每个棋子上有一个数字序号。小M的目标是将这些棋子分成 M 组,每组恰好5个,并且组内棋子的序号相同。小M希望知道是否可以按照这…...
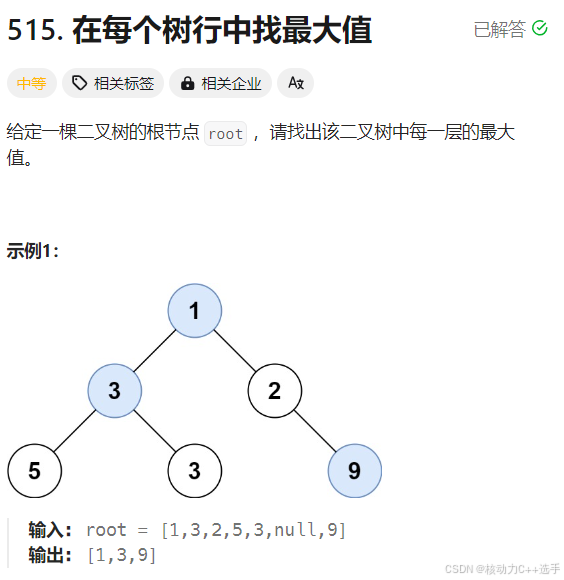
【LeetCode热题100】队列+宽搜
这篇博客是关于队列宽搜的几道题,主要包括N叉树的层序遍历、二叉树的锯齿形层序遍历、二叉树最大宽度、在每个数行中找最大值。 class Solution { public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;if(!root) …...

【阵列信号处理】相干信号和非相干信号生成
文章目录 一、总结二、知识点相干(coherent)和非相干(incoherent)信号相干信号生成代码 相关信号(correlated signal)相关信号生成代码 正交信号定义 本文记录博主的科研日记。如果对博主的其他文章感兴趣&…...

React 组件生命周期
React 组件生命周期 React 组件生命周期是React框架中一个核心概念,它描述了一个组件从创建到销毁的过程。理解组件生命周期对于高效开发React应用至关重要,因为它允许开发者在一个组件的不同阶段执行特定的逻辑。本文将详细介绍React组件的生命周期方法,并解释它们在组件的…...
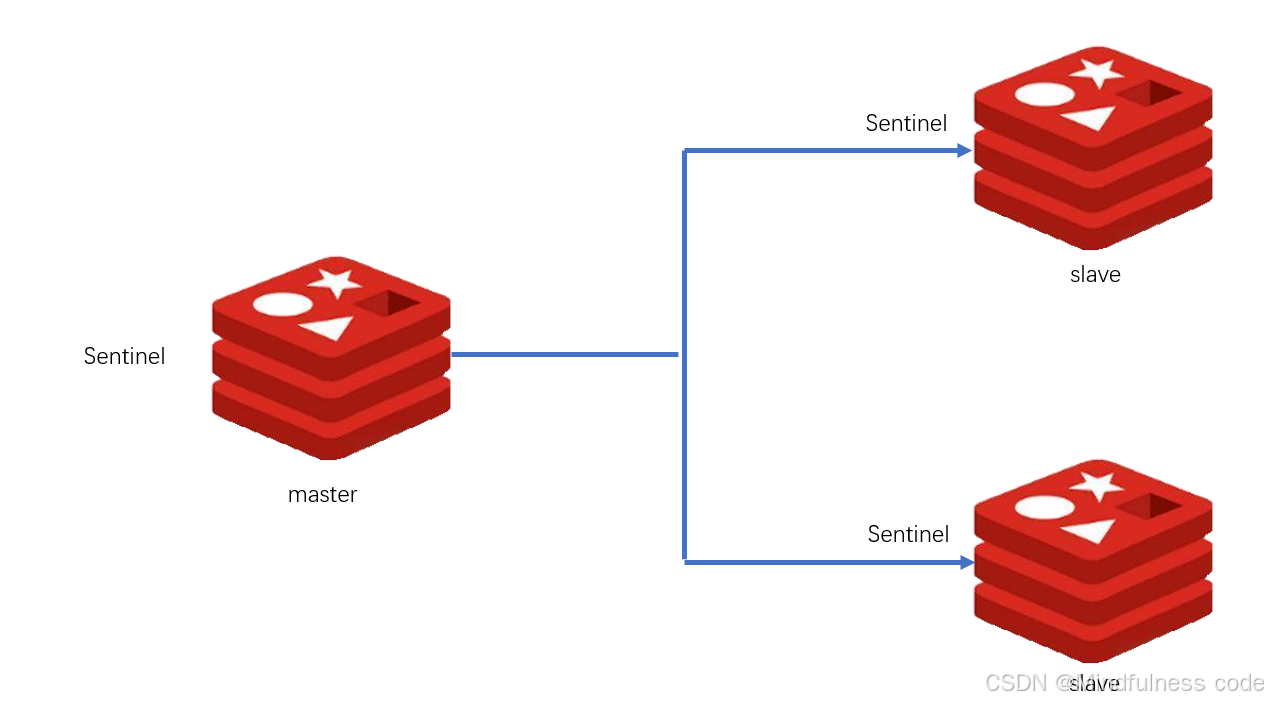
Kylin Server V10 下基于Sentinel(哨兵)实现Redis高可用集群
一、什么是哨兵模式 Redis Sentinel 是一个分布式系统,为 Redis 提供高可用性解决方案。可以在一个架构中运行多个 Sentinel 进程(progress)这些进程使用流言协议(gossip protocols)来接收关于主服务器是否下线信息,并使用投票协议(agreement protocols)来决定是否执行…...
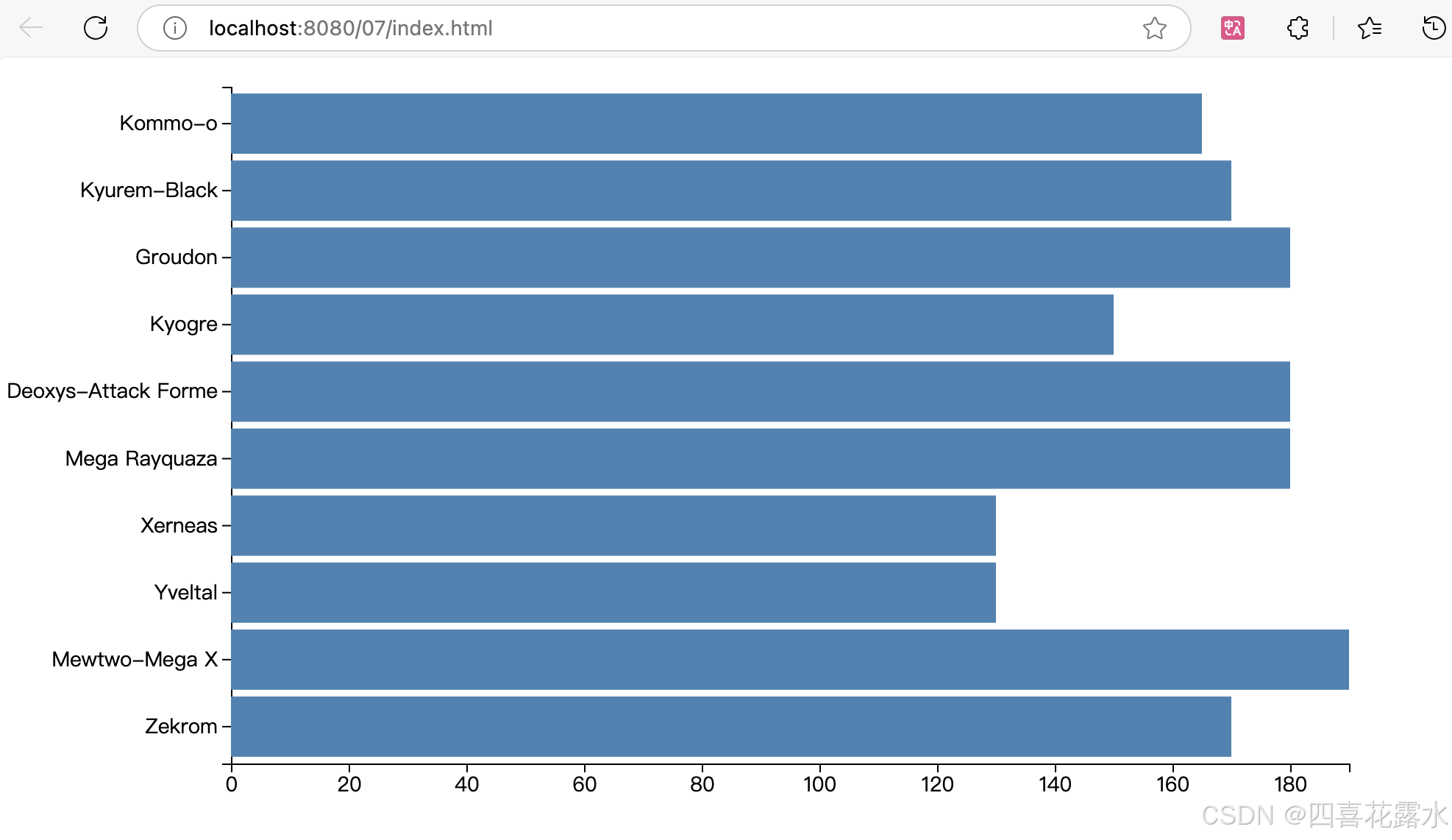
07-Making a Bar Chart with D3.js and SVG
课程链接 Curran的课程,通过 D3.js 的 scaleLinear, max, scaleBand, axisLeft, axisBottom,根据 .csv 文件生成一个横向柱状图。 【注】如果想造csv数据,可以使用通义千问,关于LinearScale与BandScale不懂的地方也可以在通义千…...

硅谷甄选前端项目环境配置笔记
此教程来自于尚硅谷 文章目录 **此教程来自于尚硅谷**硅谷甄选运营平台一、搭建后台管理系统模板1.1项目初始化1.1.1环境准备1.1.2初始化项目 1.2项目配置一、eslint配置1.1vue3环境代码校验插件1.2修改.eslintrc.cjs配置文件1.3.eslintignore忽略文件1.4运行脚本 二、配置**pr…...

6.7机器学习期末复习题
空间 样本空间 就是属性的所有可能情况,包括了一切可能出现或不可能出现的所有样本情况 版本空间&假设空间 假设空间就是在样本空间的基础上,给所有属性都加了一个通配符,表示任意即可;以及加上了一个空集,表示…...

1123--日期类
目录 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作...
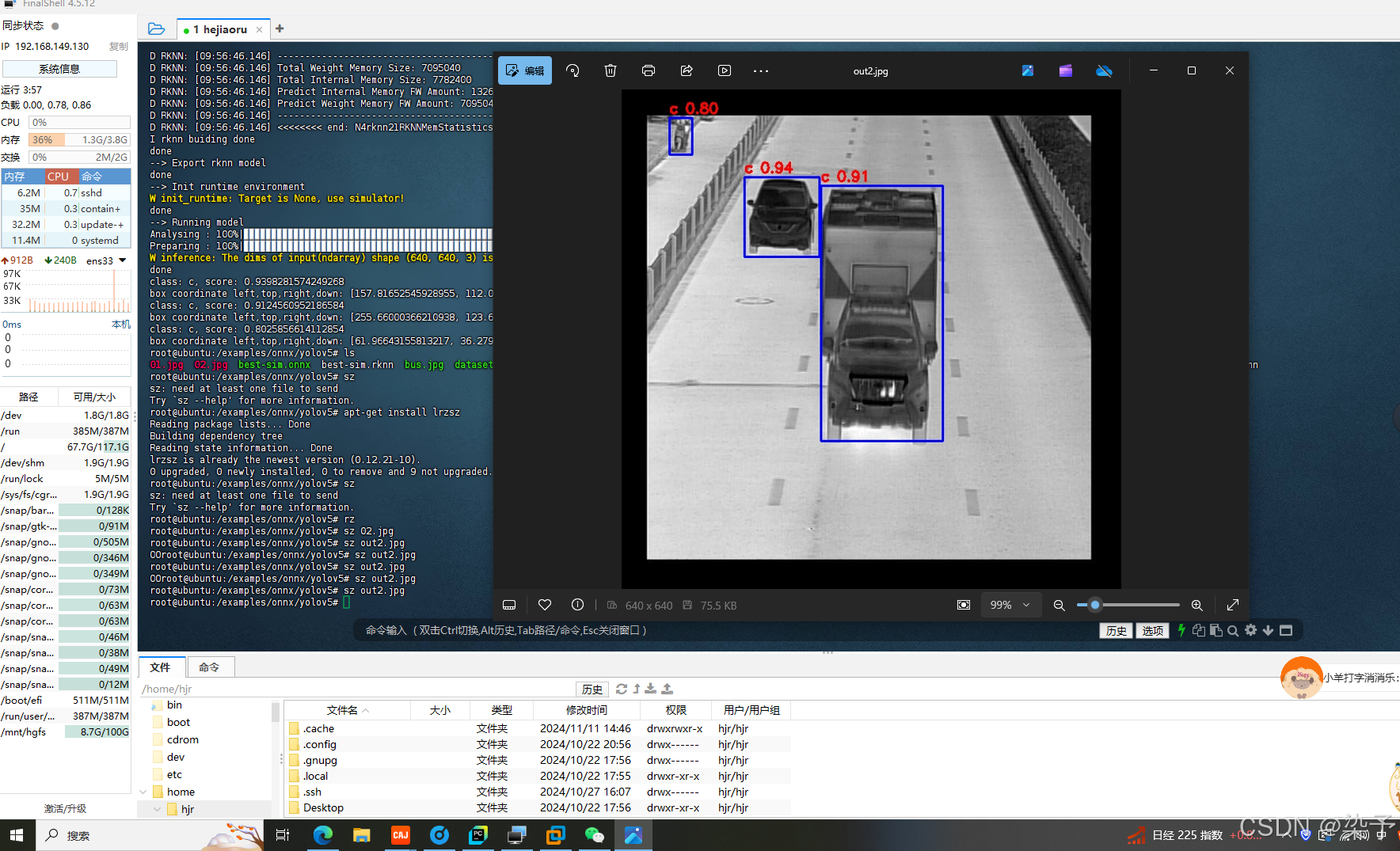
YOLOV5 /onnx模型转换成rknn
上两篇文章讲述了pytorch模型下best.pt转换成onnx模型,以及将onnx进行简化成为best-sim.onnx, 接下来这篇文章讲述如何将onnx模型转换成rknn模型,转换成该模型是为了在rk3568上运行 1.创建share文件夹 文件夹包含以下文件best-sim.onnx,rknn-tookit2-…...
Echarts+VUE饼图的使用(基础使用、多个饼图功能、单组饼图对应颜色使用)
安装:npm install echarts --save 配置:main.js // 引入echarts import * as echarts from echarts Vue.prototype.$echarts echarts一、基础饼图(直接拷贝就能出效果) <div class"big-box" ref"demoEhart"><…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
