每日一练:【动态规划算法】斐波那契数列模型之第 N 个泰波那契数(easy)
1. 第 N 个泰波那契数(easy)
1. 题目链接:1137. 第 N 个泰波那契数
2. 题目描述

3.题目分析
这题我们要求第n个泰波那契Tn的值,很明显的使用动态规划算法。
4.动态规划算法流程
1. 状态表示:
根据题目的要求及公式直接定义出状态表示:我们以第i个位置为结尾,dp表第i个位置的值表示第i个泰波那契的值。
2. 状态转移方程:
根据公式我们确定dp[i]的值或者状态通过状态表示方程表示是dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
3. dp表初始化:
从我们的递推公式可以看出, dp[i] 在i = 0 以及 i = 1 的时候是没有办法进行推导的,因
为 dp[-2] 或 dp[-1] 不是一个有效的数据。因此我们需要在填表之前,将 0, 1, 2 位置的值初始化。题目中已经告诉我们 dp[0] = 0, dp[1] = dp[2] = 1 ,我们按照题目的值初始化
4. 填表顺序:
要求dp[i]的值就要先确定dp[i - 1]、 dp[i - 2]、dp[i - 3]的值,因此dp表的填表顺序就是从左往右
5. 返回值:
题目要求第n个数的值,我们就应该返回 dp[n] 的值。
5.算法代码
class Solution {
public:int tribonacci(int n) {vector<int> dp(n + 1);if(n == 0) return 0;//对于n为0,1,2的特殊情况,我们需要处理一下防止越界if(n == 1 || n == 2) return 1;dp[0] = 0,dp[1] = 1,dp[2] = 1;for(int i = 3;i <= n;i++){dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];}return dp[n];}
};6.滚动数组优化:
我们发现在求解上述问题的过程中,我们只需要知道该位置前三的位置的值相加就行,因此开辟O(n)的空间消耗完全没有必要,我们使用滚动数组来进行优化(滚动数组只是一种形象的说法,并不一定是数组)
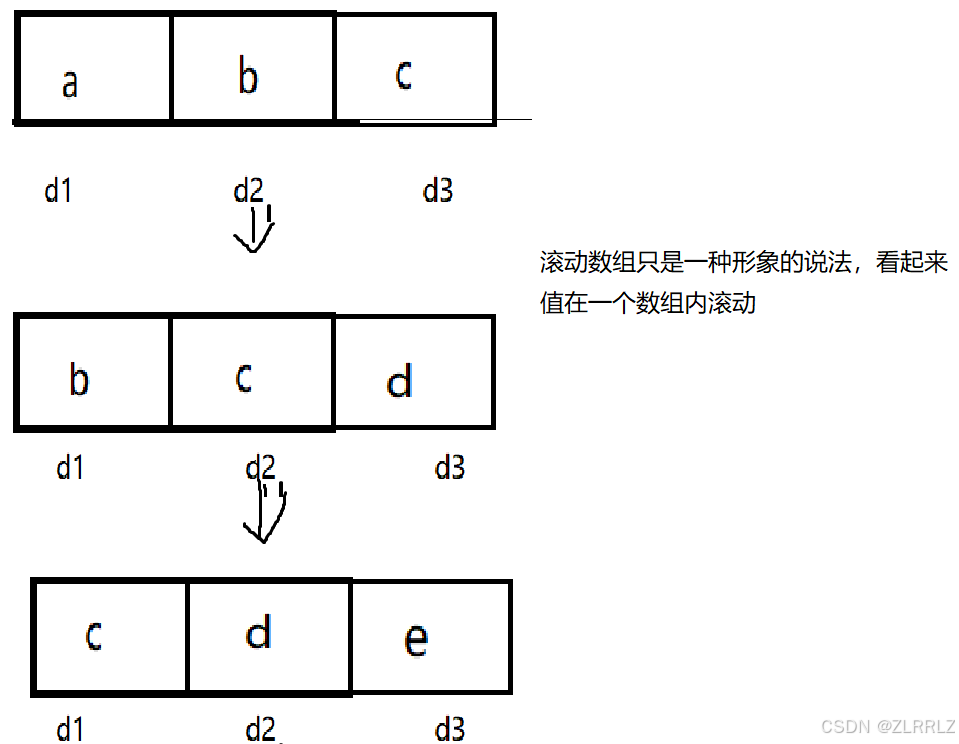
算法代码展示
class Solution {
public:int tribonacci(int n) {int a = 0,b = 1,c = 1,d = 0;if(n == 0) return 0;if(n == 1 || n == 2) return 1;for(int i = 3;i <= n;i++){d = a + b + c;a = b;b = c;c = d;}return d;}
};相关文章:

每日一练:【动态规划算法】斐波那契数列模型之第 N 个泰波那契数(easy)
1. 第 N 个泰波那契数(easy) 1. 题目链接:1137. 第 N 个泰波那契数 2. 题目描述 3.题目分析 这题我们要求第n个泰波那契Tn的值,很明显的使用动态规划算法。 4.动态规划算法流程 1. 状态表示: 根据题目的要求及公…...
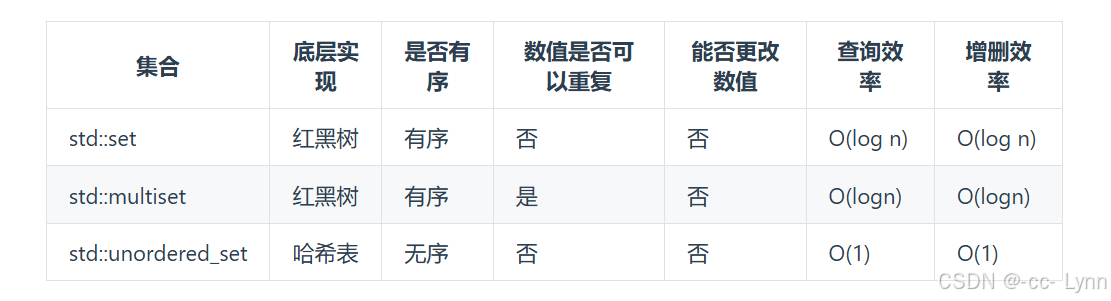
Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。 例如要查询一个名字是否在这所学校里。 要枚举的话时间复杂度是O(n),但如果使用哈希…...
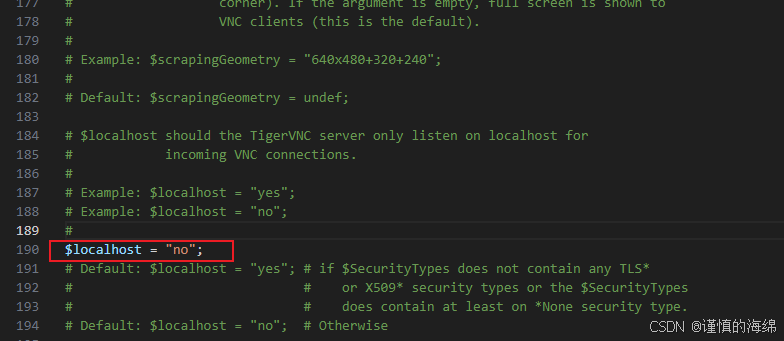
windows实现VNC连接ubuntu22.04服务器
最近弄了一个700块钱的mini主机,刷了ubuntu22.04系统,然后想要在笔记本上通过VNC连接,这样就有了一个linux的开发环境。最后实现的过程为: 安装vnc服务器 安装 VNC 服务器软件: sudo apt update sudo apt install t…...

中国电信星辰大模型:软件工厂与文生视频技术的深度解析
在科技日新月异的今天,人工智能(AI)技术正以惊人的速度改变着我们的生活和工作方式。作为这一领域的领军企业之一,中国电信凭借其强大的研发实力和深厚的技术积累,推出了星辰大模型,旨在为用户带来更加智能、高效、便捷的服务体验。本文将重点介绍中国电信星辰大模型中的…...

项目实战:基于Vue3实现一个小相册
相册的示例效果图 注意看注释... 要实现图片的相册效果,图片命名可以像{img1.jpg,img2.jpg,img3.jpg}类似于这种的命名方式。 CSS部分: <style>/* 伪元素选择器,用于在具有clear_ele类的元素内部的末尾添加一个新的元素 */.clear_ele:…...

macOS安装nvm node
macOS安装nvm macOS安装nvm创建 nvm 工作目录配置环境变量使用 nvm查看可用的 Node.js 版本安装特定版本 macOS安装nvm brew install nvm创建 nvm 工作目录 mkdir ~/.nvm配置环境变量 vim ~/.zshrc# nvm export NVM_DIR"$HOME/.nvm" [ -s "/opt/homebrew/opt…...

解决整合Django与Jinja2兼容性的问题
提问 解决整合Django与Jinja2时遇到了一些兼容性问题。已经按照常规步骤在我的settings.py中配置了Jinja2作为模板引擎,同时保留了Django默认的模板设置。然而尝试同时使用Django和Jinja2时,系统报错提示我没有指定模板。如果我尝试移除Django的默认模板…...

Elasticsearch面试内容整理-高级特性
Elasticsearch 提供了一系列高级特性,这些特性可以极大地增强其搜索、分析和管理能力,使得它在大数据场景中表现出色。以下是 Elasticsearch 的一些重要高级特性: 近实时搜索(Near Real-Time Search) Elasticsearch 的一个关键特性是 近实时搜索(NRT),这意味着数据写入…...

linux通过手工删除文件卸载oracle 11g rac的具体步骤
在linux操作系统中,有些时候我们自己学习和测试会临时搭建的oracle rac。事情完成后,我们想回收资源,需要去卸载oracle rac。为了快速卸载oracle rac,今天我们介绍下如何通过手工删除文件的方式来完成工作(操作都需要在…...
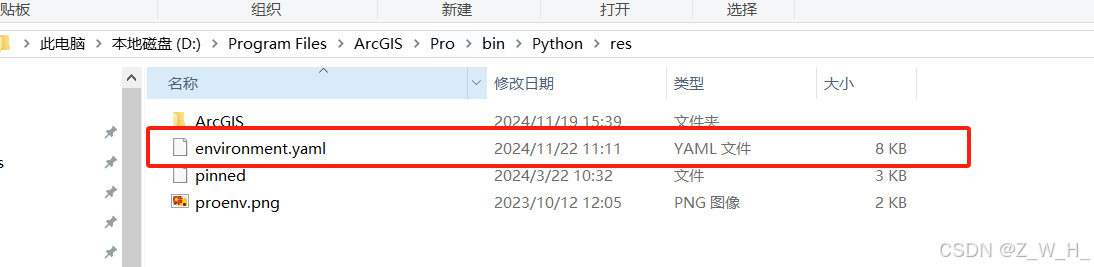
【ArcGISPro】根据yaml构建原始Pro的conda环境
使用场景 我们不小心把原始arcgispro-py3的conda环境破坏了,我们就可以使用以下方法进行修复 查找文件 在arcgis目录下找到yaml文件 如果没找到请复制以下内容到新的yaml文件 channels: - esri - defaults dependencies: - anyio=4.2.0=py311haa95532_0 - appdirs=1.4.4=p…...
刷题笔记15
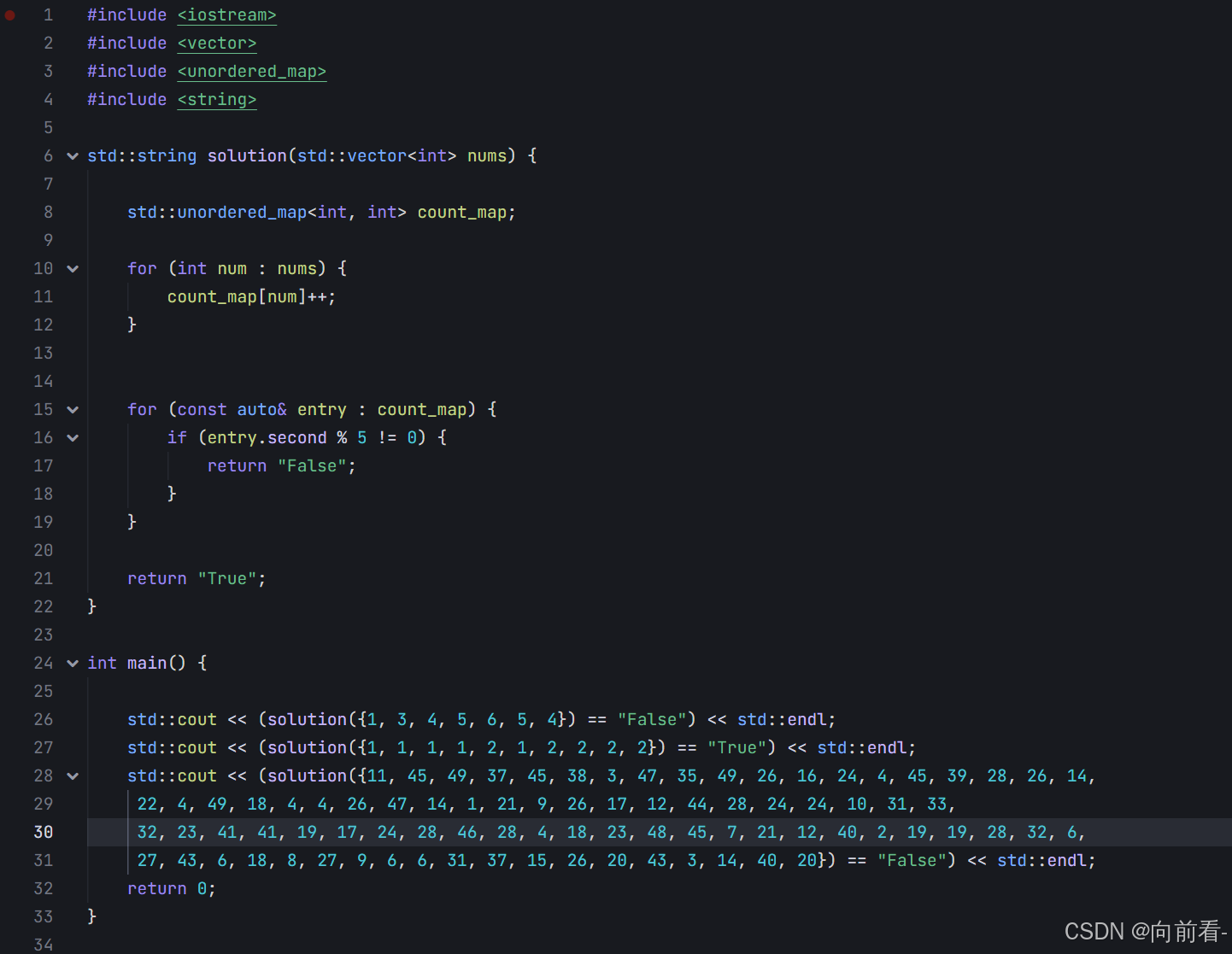
问题描述 小M和小F在玩飞行棋。游戏结束后,他们需要将桌上的飞行棋棋子分组整理好。现在有 N 个棋子,每个棋子上有一个数字序号。小M的目标是将这些棋子分成 M 组,每组恰好5个,并且组内棋子的序号相同。小M希望知道是否可以按照这…...
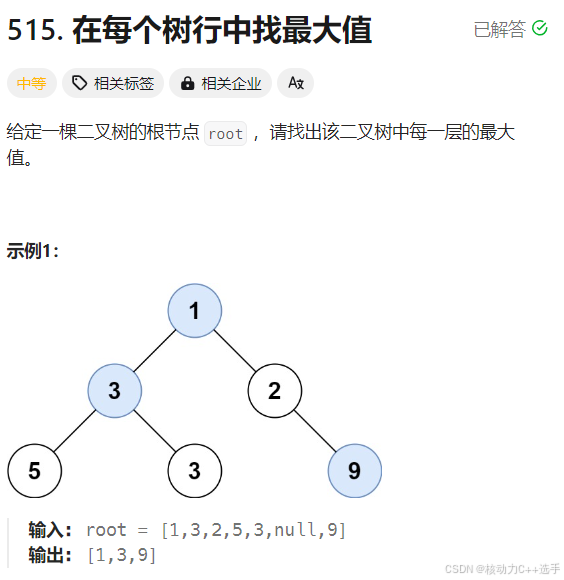
【LeetCode热题100】队列+宽搜
这篇博客是关于队列宽搜的几道题,主要包括N叉树的层序遍历、二叉树的锯齿形层序遍历、二叉树最大宽度、在每个数行中找最大值。 class Solution { public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;if(!root) …...

【阵列信号处理】相干信号和非相干信号生成
文章目录 一、总结二、知识点相干(coherent)和非相干(incoherent)信号相干信号生成代码 相关信号(correlated signal)相关信号生成代码 正交信号定义 本文记录博主的科研日记。如果对博主的其他文章感兴趣&…...

React 组件生命周期
React 组件生命周期 React 组件生命周期是React框架中一个核心概念,它描述了一个组件从创建到销毁的过程。理解组件生命周期对于高效开发React应用至关重要,因为它允许开发者在一个组件的不同阶段执行特定的逻辑。本文将详细介绍React组件的生命周期方法,并解释它们在组件的…...
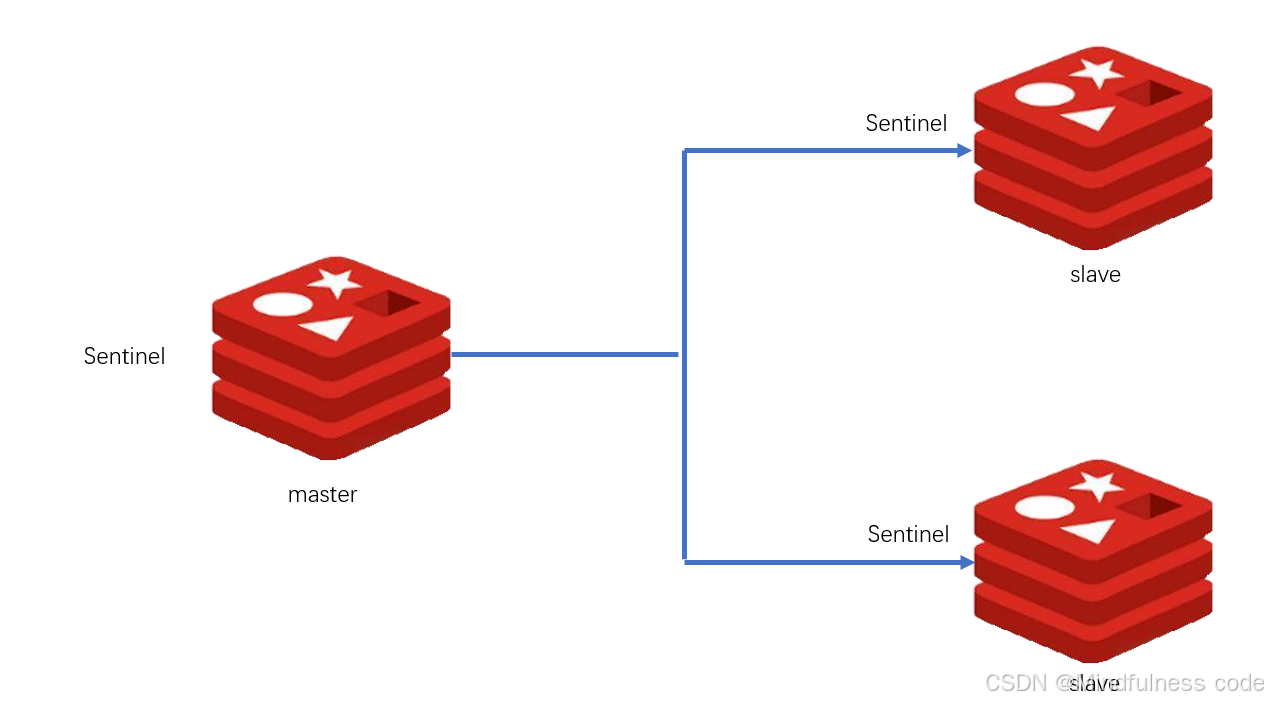
Kylin Server V10 下基于Sentinel(哨兵)实现Redis高可用集群
一、什么是哨兵模式 Redis Sentinel 是一个分布式系统,为 Redis 提供高可用性解决方案。可以在一个架构中运行多个 Sentinel 进程(progress)这些进程使用流言协议(gossip protocols)来接收关于主服务器是否下线信息,并使用投票协议(agreement protocols)来决定是否执行…...
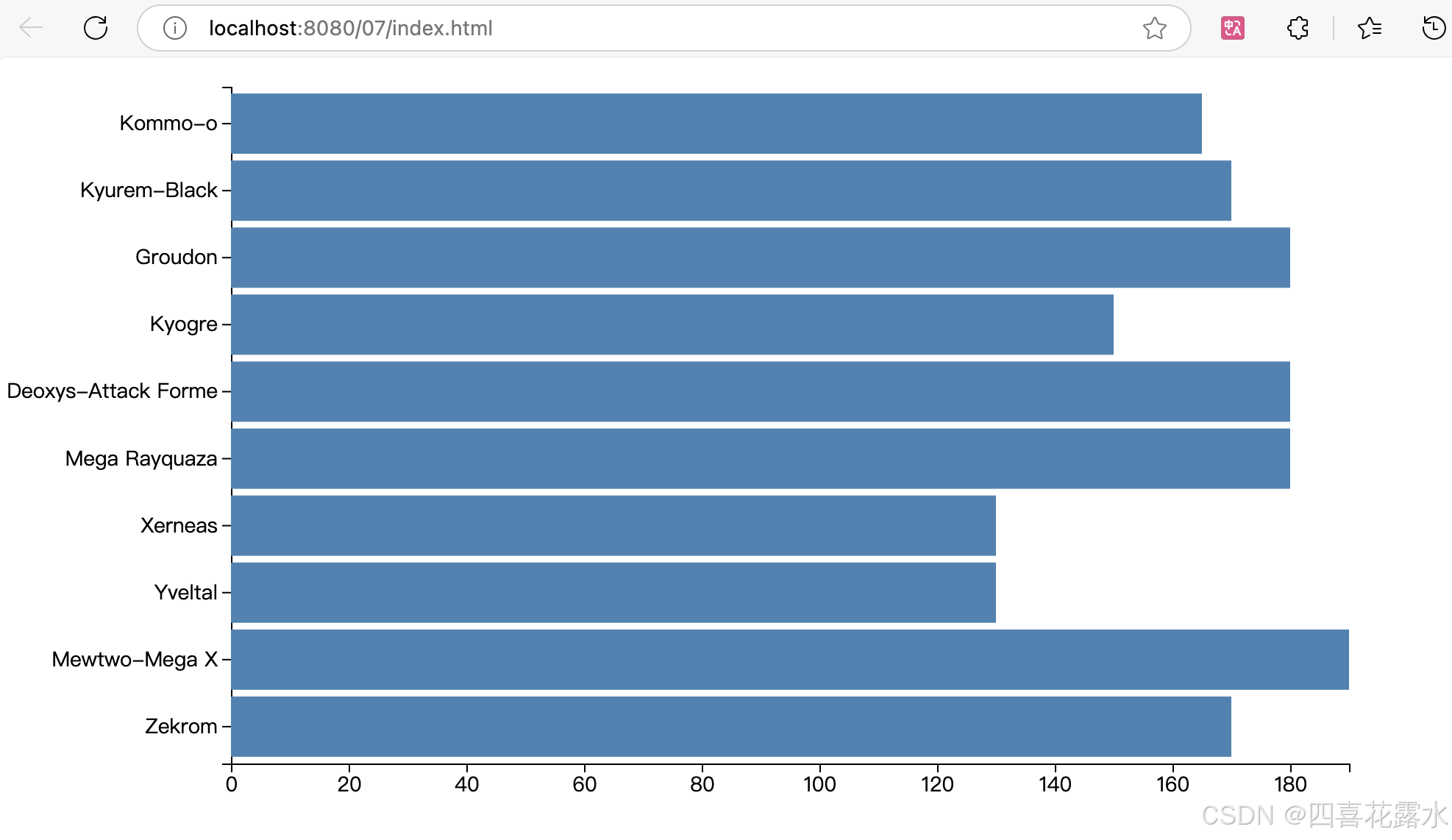
07-Making a Bar Chart with D3.js and SVG
课程链接 Curran的课程,通过 D3.js 的 scaleLinear, max, scaleBand, axisLeft, axisBottom,根据 .csv 文件生成一个横向柱状图。 【注】如果想造csv数据,可以使用通义千问,关于LinearScale与BandScale不懂的地方也可以在通义千…...

硅谷甄选前端项目环境配置笔记
此教程来自于尚硅谷 文章目录 **此教程来自于尚硅谷**硅谷甄选运营平台一、搭建后台管理系统模板1.1项目初始化1.1.1环境准备1.1.2初始化项目 1.2项目配置一、eslint配置1.1vue3环境代码校验插件1.2修改.eslintrc.cjs配置文件1.3.eslintignore忽略文件1.4运行脚本 二、配置**pr…...

6.7机器学习期末复习题
空间 样本空间 就是属性的所有可能情况,包括了一切可能出现或不可能出现的所有样本情况 版本空间&假设空间 假设空间就是在样本空间的基础上,给所有属性都加了一个通配符,表示任意即可;以及加上了一个空集,表示…...

1123--日期类
目录 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作...
YOLOV5 /onnx模型转换成rknn
上两篇文章讲述了pytorch模型下best.pt转换成onnx模型,以及将onnx进行简化成为best-sim.onnx, 接下来这篇文章讲述如何将onnx模型转换成rknn模型,转换成该模型是为了在rk3568上运行 1.创建share文件夹 文件夹包含以下文件best-sim.onnx,rknn-tookit2-…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...
