图论最短路(floyed+ford)
Floyd 算法简介
Floyd 算法(也称为 Floyd-Warshall 算法)是一种动态规划算法,用于解决所有节点对之间的最短路径问题。它可以同时处理加权有向图和无向图,包括存在负权边的情况(只要没有负权环)。
核心思想
Floyd 算法的基本思想是利用动态规划,通过逐步引入中间节点优化路径,最终得到每对节点之间的最短路径。
假设图的节点编号为 1,2,…,n,dist[i][j] 表示节点 i 到节点 j 的当前最短路径长度,算法通过以下递推公式更新 dist[i][j]:
dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j])其中:
- i:起点
- j:终点
- k:中间节点
含义:判断是否通过节点 k 可以使 i 到 j 的路径更短,如果更短,则更新。
算法流程
-
初始化距离矩阵
dist:- 如果 i=j,
dist[i][j] = 0(自身到自身的距离为 0)。 - 如果 i≠j 且存在边 (i,j),
dist[i][j] = data(边的权值)。 - 如果 i≠j 且不存在边 (i,j),
dist[i][j] = INT_MAX(表示无穷大,路径不存在)。
- 如果 i=j,
-
动态规划:
- 依次引入节点 k(k=1,2,…,n)作为中间节点,更新所有节点对之间的最短路径。
- 按公式更新 dist[i][j]。
-
检查结果:
- 遍历
dist矩阵,获得任意两点之间的最短路径。 - 如果对角线上的
dist[i][i] < 0,说明存在负权环。
- 遍历
代码
#include <bits/stdc++.h>
using namespace std;
int dis[110][110],n,m,a,b,want1,want2;
int main()
{cout<<"请输入点数,边数"<<endl;cin>>n>>m;cout<<"输入a点到b点的距离"<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dis[i][j]=100000;}}for(int i=1;i<=m;i++){cin>>a>>b;cin>>dis[a][b];dis[b][a]=dis[a][b];}cout<<"输入想查找的两个点的编号"<<endl; cin>>want1>>want2;for(int k=1;k<=n;++k){for(int i=1;i<=n;++i){for(int j=1;j<=n;++j){if(dis[i][j]>dis[i][k]+dis[k][j]){dis[i][j]=dis[i][k]+dis[k][j]; }}}}cout<<want1<<"->"<<want2<<"最短的距离为"<<dis[want1][want2];return 0;
}Ford 算法简介
Ford 算法(通常指 Bellman-Ford 算法)是一种用于计算单源最短路径的经典算法。它可以在加权有向图中找到从一个源点到所有其他节点的最短路径,支持负权边,并且能够检测负权环。
算法思想
Bellman-Ford 算法的核心思想是通过松弛操作(Relaxation),逐步更新最短路径估计值。它基于以下性质:
- 如果存在从节点 u 到节点 v 的边 (u,v,w),并且通过这条边可以缩短路径,那么更新路径长度:
dist[v]=min(dist[v],dist[u]+w)
算法执行 n−1 次松弛操作(n 为节点数),确保找到从源点到所有节点的最短路径(若无负权环)。
算法流程
-
初始化:
- 将源点的距离设为 0(
dist[src] = 0)。 - 其他节点的初始距离设为无穷大(
dist[i] = \infty)。
- 将源点的距离设为 0(
-
松弛所有边:
- 重复 n−1 次(最多需要 n−1 次遍历,因为最短路径最多包含 n−1 条边)。
- 对图中每条边 (u,v,w),尝试更新节点 vvv 的距离。
-
检查负权环:
- 再次遍历所有边。如果发现还能继续松弛,说明存在负权环。
代码
#include <bits/stdc++.h>
using namespace std;
int d[110],n,m,s=1,k;
struct Theedge
{int start,end,data;
}edge[110];
int main()
{cin>>n>>m>>s>>k;for(int i=1;i<=m;i++){cin>>edge[i].start>>edge[i].end>>edge[i].data;}for(int i=1;i<=n;i++){d[i]=100000;}d[s]=0;for(int i=1;i<=n-1;i++){for(int j=1;j<=m;j++){int x=edge[j].start;int y=edge[j].end;int z=edge[j].data;d[y]=min(d[y],d[x]+z);d[x]=min(d[x],d[y]+z);}}cout<<d[k];return 0;
}
相关文章:
)
图论最短路(floyed+ford)
Floyd 算法简介 Floyd 算法(也称为 Floyd-Warshall 算法)是一种动态规划算法,用于解决所有节点对之间的最短路径问题。它可以同时处理加权有向图和无向图,包括存在负权边的情况(只要没有负权环)。 核心思…...

BERT的中文问答系统39
实现当用户在GUI中输入问题(例如“刘邦”)且输出的答案被标记为不正确时,自动从百度百科中搜索相关内容并显示在GUI中的功能,我们需要对现有的代码进行一些修改。以下是完整的代码,包括对XihuaChatbotGUI类的修改以及新…...

从 Mac 远程控制 Windows:一站式配置与实践指南20241123
引言:跨平台操作的需求与挑战 随着办公场景的多样化,跨平台操作成为现代开发者和 IT 人员的刚需。从 Mac 系统远程控制 Windows,尤其是在同一局域网下,是一种高效解决方案。不仅能够灵活管理资源,还可以通过命令行简化…...
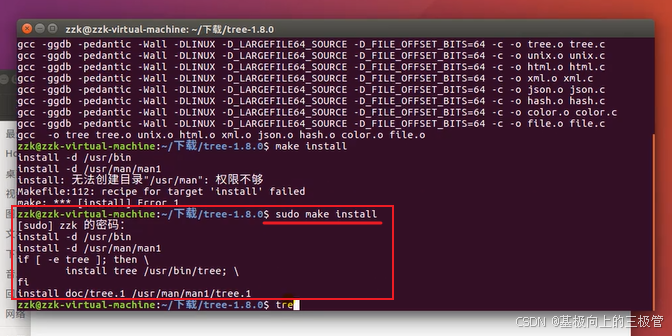
【Linux学习】【Ubuntu入门】1-5 ubuntu软件安装
1.使用sudo apt-get install vim:安装vim编辑器。 参考安装 安装时可能会遇到的问题 2.deb软件安装命令sudo dpkg -i xxx.deb 下载软件安装包时下载Linux版本,在Ubuntu中双击deb文件或者输入命令sudo dpkg -i xxx.deb,xxx.deb为安装包名称…...

如何自动下载和更新冰狐智能辅助?
冰狐智能辅助的版本更新非常快,如果设备多的话每次手工更新会非常麻烦,现在分享一种免费的自动下载和安装冰狐智能辅助的方法。 一、安装迅雷浏览器 安装迅雷浏览器1.19.0.4280版本,浏览器用于打开冰狐的官网,以便于从官网下载a…...

动态渲染页面爬取
我们可以直接使用模拟浏览器运行的方式来实现,这样就可以做到在浏览器中看到是什么样,抓取的源码就是什么样,也就是可见即可爬。这样我们就不用再去管网页内部的 JavaScript 用了什么算法渲染页面,不用管网页后台的 Ajax 接口到底…...

C++适配器模式之可插入适配器的实现模式和方法
可插入适配器与Adaptee的窄接口 在C适配器模式中,可插入适配器(Pluggable Adapter)是指适配器类的设计允许在运行时动态地插入不同的Adaptee对象,从而使适配器具有灵活性和可扩展性。这种设计使得适配器不仅限于适配一个特定的Ad…...
每日一练:【动态规划算法】斐波那契数列模型之第 N 个泰波那契数(easy)
1. 第 N 个泰波那契数(easy) 1. 题目链接:1137. 第 N 个泰波那契数 2. 题目描述 3.题目分析 这题我们要求第n个泰波那契Tn的值,很明显的使用动态规划算法。 4.动态规划算法流程 1. 状态表示: 根据题目的要求及公…...
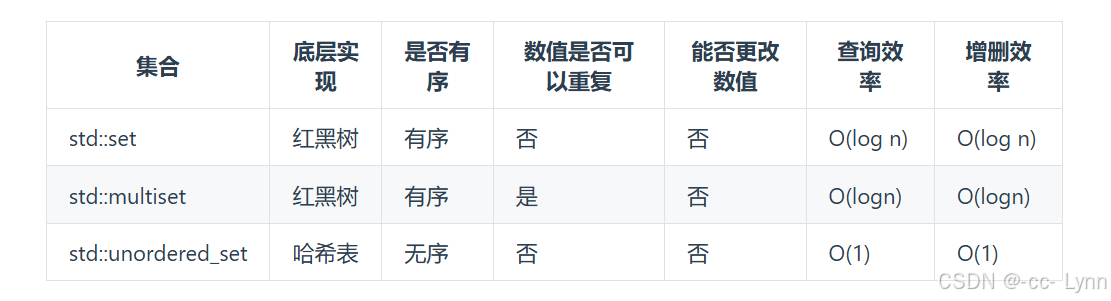
Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。 例如要查询一个名字是否在这所学校里。 要枚举的话时间复杂度是O(n),但如果使用哈希…...
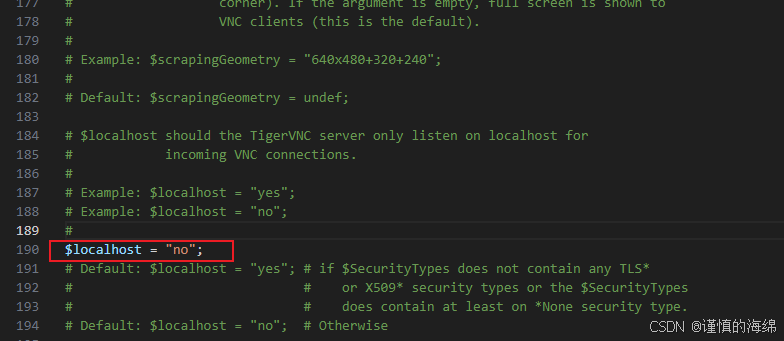
windows实现VNC连接ubuntu22.04服务器
最近弄了一个700块钱的mini主机,刷了ubuntu22.04系统,然后想要在笔记本上通过VNC连接,这样就有了一个linux的开发环境。最后实现的过程为: 安装vnc服务器 安装 VNC 服务器软件: sudo apt update sudo apt install t…...

中国电信星辰大模型:软件工厂与文生视频技术的深度解析
在科技日新月异的今天,人工智能(AI)技术正以惊人的速度改变着我们的生活和工作方式。作为这一领域的领军企业之一,中国电信凭借其强大的研发实力和深厚的技术积累,推出了星辰大模型,旨在为用户带来更加智能、高效、便捷的服务体验。本文将重点介绍中国电信星辰大模型中的…...

项目实战:基于Vue3实现一个小相册
相册的示例效果图 注意看注释... 要实现图片的相册效果,图片命名可以像{img1.jpg,img2.jpg,img3.jpg}类似于这种的命名方式。 CSS部分: <style>/* 伪元素选择器,用于在具有clear_ele类的元素内部的末尾添加一个新的元素 */.clear_ele:…...

macOS安装nvm node
macOS安装nvm macOS安装nvm创建 nvm 工作目录配置环境变量使用 nvm查看可用的 Node.js 版本安装特定版本 macOS安装nvm brew install nvm创建 nvm 工作目录 mkdir ~/.nvm配置环境变量 vim ~/.zshrc# nvm export NVM_DIR"$HOME/.nvm" [ -s "/opt/homebrew/opt…...

解决整合Django与Jinja2兼容性的问题
提问 解决整合Django与Jinja2时遇到了一些兼容性问题。已经按照常规步骤在我的settings.py中配置了Jinja2作为模板引擎,同时保留了Django默认的模板设置。然而尝试同时使用Django和Jinja2时,系统报错提示我没有指定模板。如果我尝试移除Django的默认模板…...

Elasticsearch面试内容整理-高级特性
Elasticsearch 提供了一系列高级特性,这些特性可以极大地增强其搜索、分析和管理能力,使得它在大数据场景中表现出色。以下是 Elasticsearch 的一些重要高级特性: 近实时搜索(Near Real-Time Search) Elasticsearch 的一个关键特性是 近实时搜索(NRT),这意味着数据写入…...

linux通过手工删除文件卸载oracle 11g rac的具体步骤
在linux操作系统中,有些时候我们自己学习和测试会临时搭建的oracle rac。事情完成后,我们想回收资源,需要去卸载oracle rac。为了快速卸载oracle rac,今天我们介绍下如何通过手工删除文件的方式来完成工作(操作都需要在…...
【ArcGISPro】根据yaml构建原始Pro的conda环境
使用场景 我们不小心把原始arcgispro-py3的conda环境破坏了,我们就可以使用以下方法进行修复 查找文件 在arcgis目录下找到yaml文件 如果没找到请复制以下内容到新的yaml文件 channels: - esri - defaults dependencies: - anyio=4.2.0=py311haa95532_0 - appdirs=1.4.4=p…...
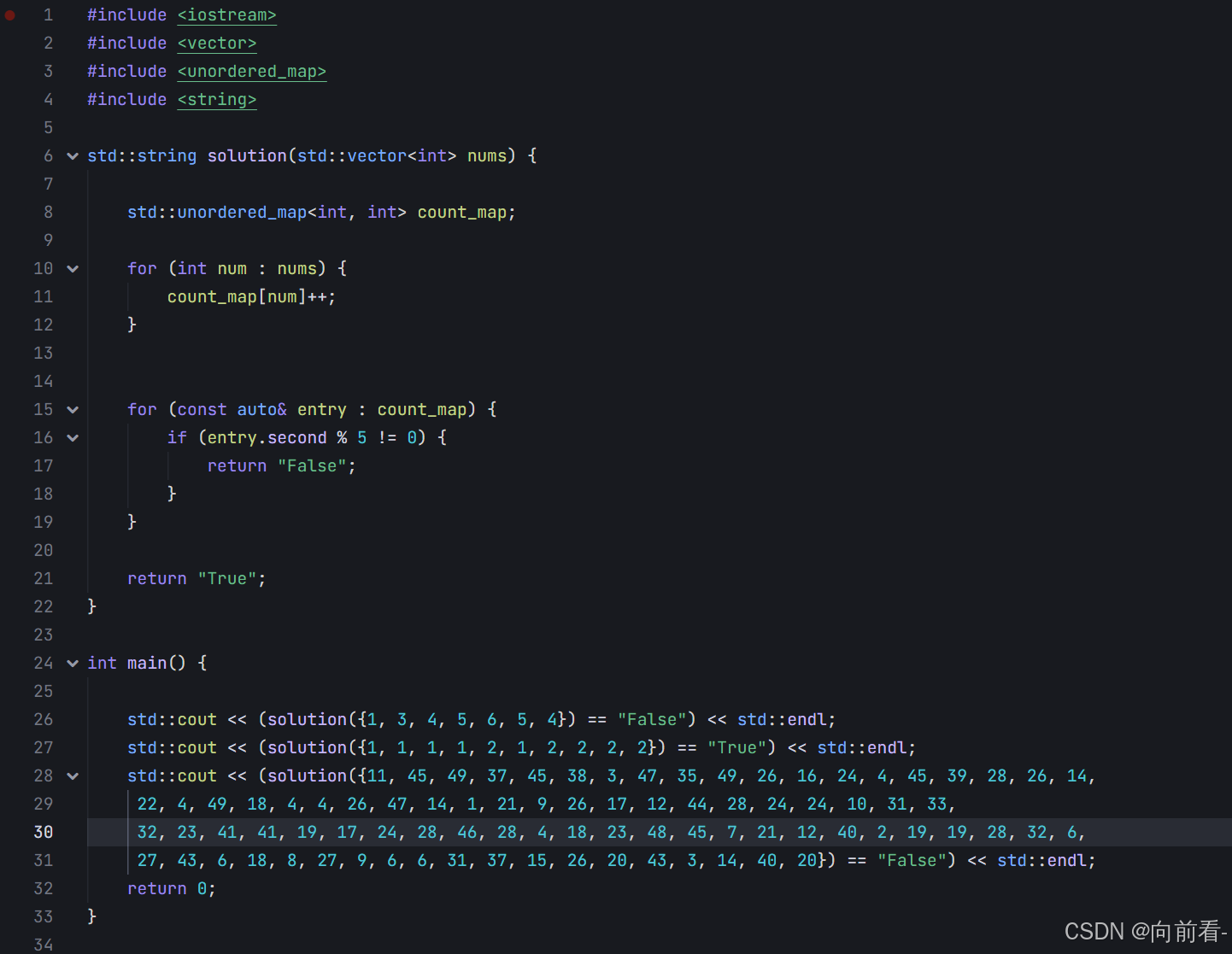
刷题笔记15
问题描述 小M和小F在玩飞行棋。游戏结束后,他们需要将桌上的飞行棋棋子分组整理好。现在有 N 个棋子,每个棋子上有一个数字序号。小M的目标是将这些棋子分成 M 组,每组恰好5个,并且组内棋子的序号相同。小M希望知道是否可以按照这…...
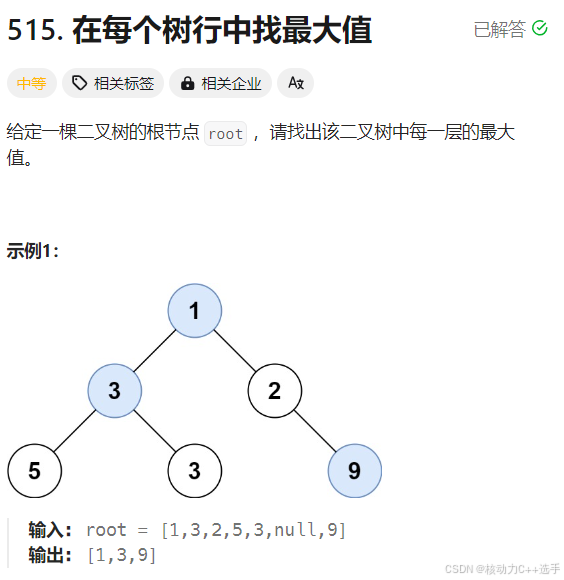
【LeetCode热题100】队列+宽搜
这篇博客是关于队列宽搜的几道题,主要包括N叉树的层序遍历、二叉树的锯齿形层序遍历、二叉树最大宽度、在每个数行中找最大值。 class Solution { public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;if(!root) …...

【阵列信号处理】相干信号和非相干信号生成
文章目录 一、总结二、知识点相干(coherent)和非相干(incoherent)信号相干信号生成代码 相关信号(correlated signal)相关信号生成代码 正交信号定义 本文记录博主的科研日记。如果对博主的其他文章感兴趣&…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
