C++知识点总结(58):序列型动态规划
动态规划Ⅰ
- 一、基础
- 1. 意义
- 2. 序列 dp 解法
- 二、例题
- 1. 最大子段和
- 2. 删数最大子段和(数据强度:pro max)
- 3. 最长上升子序列(数据强度:pro max)
- 4. 3 或 5 的倍数序列
- 5. 数码约数序列
一、基础
1. 意义
动态规划(dynamic programming,简称 dp),将一个目标大问题“大事化小,小事化了”,分成很多的子问题,得出子问题的解后得到目标大问题的解。动态规划相当于地狱难度的递推。
2. 序列 dp 解法
序列型动态规划分为几种常见的问题:
- 取连续的子段(串)
dp[i]表示以 i i i 为结尾
- 取子序列(不要求连续)
dp[i]表示以 i i i 为结尾dp[i]表示 0 ∼ i 0\sim i 0∼i 中 …dp[i]长度为 i i i 序列结尾的性质
- 分段
dp[i]表示以 i i i 为结尾
二、例题
1. 最大子段和
题目描述
给出数组 a a a,如果我们取连续且非空的一段,那么这段的和最大是多少?
输入描述
第 1 1 1 行,是一个正整数 n n n,数组 a a a 的长度。
第 2 2 2 行,用空格隔开的 n n n 个整数,依次是 a [ 1 ] ∼ a [ n ] a[1]\sim a[n] a[1]∼a[n] 的值。
输出描述
1 1 1 个整数,为所求的最大的和
样例1
输入
6 1 -6 5 -4 2 4输出
7
提示
【样例解释】
取 5 , − 4 , 2 , 4 5,−4,2,4 5,−4,2,4 可以得到最大的和 7 7 7。
【数据范围】
对于 60 % 60\% 60% 的数据, n ≤ 100 n≤100 n≤100。
对于 80 % 80\% 80% 的数据, n ≤ 5000 n≤5000 n≤5000。
对于 100 % 100\% 100% 的数据, n ≤ 100000 n≤100000 n≤100000。
【问题类型】 取子段
【问题解法】 dp[i] 表示以 a[i] 为结尾的最大子段和是多少
【模板技巧】 如果前面都是负数,我不跟它们同流合污(a[i]);如果前面大的,那就加入它们,做一个更大的数(dp[i-1]+a[i])
【参考答案】
#include<bits/stdc++.h>
using namespace std;
int n,maxn=-1e8;
int a[100005];
int dp[100005];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];dp[1]=a[1];for(int i=2;i<=n;i++){dp[i]=max(a[i],dp[i-1]+a[i]);maxn=max(maxn,dp[i]);}cout<<maxn;return 0;
}
2. 删数最大子段和(数据强度:pro max)
给出一个数组 a[],删除一个元素后,求它的最大子段和。(子段是指数组中连续的一段元素)删除的元素可以由你自由选择,但是不能不删除任何元素,输出你能得到的最大的子段和。
思路:要删掉 a[i] 的时候会产生两个切口,第一个是以 a[i-1] 为结尾,第二个是以 a[i+1] 为开头。以 a[i-1] 为结尾取一个非常大的子段,以 a[i+1] 为开头取一个非常大的子段,将它们组合在一起,就可以完成本题。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e6+8;
const int NEGINF=-1e18;
int n,ans=NEGINF;
int a[MAXN],dpl[MAXN],dpr[MAXN];
/*
* dpl[i]:以i为右端点的最大子段和
* dpr[i]:以i为左端点的最大子段和
*/
signed main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)dpl[i]=max(dpl[i-1]+a[i],a[i]);for(int i=n;i>=1;i--)dpr[i]=max(dpr[i+1]+a[i],a[i]);for(int i=1;i<=n;i++)ans=max({ans,dpl[i-1],dpr[i+1],dpl[i-1]+dpr[i+1]});//选择左边/右边/左边和右边cout<<ans;return 0;
}
3. 最长上升子序列(数据强度:pro max)
求出数组 a[] 的最长上升子序列⻓度。
参考答案:
#include<bits/stdc++.h>
using namespace std;
int n,sz;
int a[5005];
int dp[5005];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){if(sz==0||a[i]>dp[sz])sz++,dp[sz]=a[i];else{int p=lower_bound(dp+1,dp+sz+1,a[i])-dp;dp[p]=a[i];}}cout<<sz;return 0;
}
4. 3 或 5 的倍数序列
给出一个序列 a[],要求你从中找出一个子序列,满足子序列中任意相邻两数之和是 3 3 3 或 5 5 5 的倍数。
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e3+8;
const int MOD=1e9+7;
int n,a[MAXN],dp[MAXN];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int ans=0;for(int i=1;i<=n;i++){for(int j=1;j<i;j++)if((a[i]+a[j])%3==0||(a[i]+a[j])%5==0)dp[i]=(dp[i]+dp[j]+1)%MOD;ans=(ans+dp[i])%MOD;}cout<<ans;return 0;
}
5. 数码约数序列
给出一个序列 a[],要求你从中找出一个子序列,满足子序列中任意相邻两数,前一个数的末位数码是后一个数的首位数码的约数。
例如 302 , 817 , 739000 302,817,739000 302,817,739000 是一个满足要求的序列,因为 302 302 302 的末位 2 2 2 是 807 807 807 的首位 8 8 8 的约数; 817 817 817 的末位 7 7 7 是 739000 739000 739000 的首位 7 7 7 的约数。 但是 70 , 1 70,1 70,1 就不满足要求,因为 0 0 0 不是 1 1 1 的约数。
问所有满足要求的子序列中,总和最大的序列的和是多少?(单独一个数也算满足要求的序列)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+8;
long long n,dp[MAXN][10];
int main(){cin>>n;for(int i=1,a,fst,lst;i<=n;i++){cin>>a,fst=a,lst=a%10;while(fst>=10)fst/=10;for(int j=0;j<=9;j++)dp[i][j]=dp[i-1][j];for(int j=1;j<=fst;j++)if(fst%j==0)dp[i][lst]=max(dp[i][lst],dp[i-1][j]+a);}long long ans=0;for(int i=0;i<=9;i++)ans=max(ans,dp[n][i]);cout<<ans;return 0;
}
相关文章:
:序列型动态规划)
C++知识点总结(58):序列型动态规划
动态规划Ⅰ 一、基础1. 意义2. 序列 dp 解法 二、例题1. 最大子段和2. 删数最大子段和(数据强度:pro max)3. 最长上升子序列(数据强度:pro max)4. 3 或 5 的倍数序列5. 数码约数序列 一、基础 1. 意义 动…...
使用)
go interface(接口)使用
在 Go 语言中,接口(interface)是一种抽象类型,它定义了一组方法,但是不实现这些方法。接口指定了一个对象的行为,而不关心对象的具体实现。接口使得代码更加灵活和可扩展。 定义接口 接口使用 type 关键字…...

【docker】docker commit 命令 将当前容器的状态保存为一个新的镜像
在Docker容器中安装了许多软件,并希望将当前容器的状态保存为一个新的镜像,可以使用docker commit命令来创建一个新的镜像。以下是如何操作的步骤: 找到容器ID或名称: 首先,需要找到想要保存的容器的ID或名称。可以使用…...

使用 Java 中的 `String.format` 方法格式化字符串
前言 在编程过程中,我们经常需要创建格式化的字符串来满足特定的需求,比如生成用户友好的消息、构建报告或是输出调试信息。Java 提供了一个强大的工具——String.format 方法,它可以帮助我们轻松地完成这些任务。 String.format 方法简介 …...
)
图论最短路(floyed+ford)
Floyd 算法简介 Floyd 算法(也称为 Floyd-Warshall 算法)是一种动态规划算法,用于解决所有节点对之间的最短路径问题。它可以同时处理加权有向图和无向图,包括存在负权边的情况(只要没有负权环)。 核心思…...

BERT的中文问答系统39
实现当用户在GUI中输入问题(例如“刘邦”)且输出的答案被标记为不正确时,自动从百度百科中搜索相关内容并显示在GUI中的功能,我们需要对现有的代码进行一些修改。以下是完整的代码,包括对XihuaChatbotGUI类的修改以及新…...

从 Mac 远程控制 Windows:一站式配置与实践指南20241123
引言:跨平台操作的需求与挑战 随着办公场景的多样化,跨平台操作成为现代开发者和 IT 人员的刚需。从 Mac 系统远程控制 Windows,尤其是在同一局域网下,是一种高效解决方案。不仅能够灵活管理资源,还可以通过命令行简化…...
【Linux学习】【Ubuntu入门】1-5 ubuntu软件安装
1.使用sudo apt-get install vim:安装vim编辑器。 参考安装 安装时可能会遇到的问题 2.deb软件安装命令sudo dpkg -i xxx.deb 下载软件安装包时下载Linux版本,在Ubuntu中双击deb文件或者输入命令sudo dpkg -i xxx.deb,xxx.deb为安装包名称…...

如何自动下载和更新冰狐智能辅助?
冰狐智能辅助的版本更新非常快,如果设备多的话每次手工更新会非常麻烦,现在分享一种免费的自动下载和安装冰狐智能辅助的方法。 一、安装迅雷浏览器 安装迅雷浏览器1.19.0.4280版本,浏览器用于打开冰狐的官网,以便于从官网下载a…...

动态渲染页面爬取
我们可以直接使用模拟浏览器运行的方式来实现,这样就可以做到在浏览器中看到是什么样,抓取的源码就是什么样,也就是可见即可爬。这样我们就不用再去管网页内部的 JavaScript 用了什么算法渲染页面,不用管网页后台的 Ajax 接口到底…...

C++适配器模式之可插入适配器的实现模式和方法
可插入适配器与Adaptee的窄接口 在C适配器模式中,可插入适配器(Pluggable Adapter)是指适配器类的设计允许在运行时动态地插入不同的Adaptee对象,从而使适配器具有灵活性和可扩展性。这种设计使得适配器不仅限于适配一个特定的Ad…...
每日一练:【动态规划算法】斐波那契数列模型之第 N 个泰波那契数(easy)
1. 第 N 个泰波那契数(easy) 1. 题目链接:1137. 第 N 个泰波那契数 2. 题目描述 3.题目分析 这题我们要求第n个泰波那契Tn的值,很明显的使用动态规划算法。 4.动态规划算法流程 1. 状态表示: 根据题目的要求及公…...
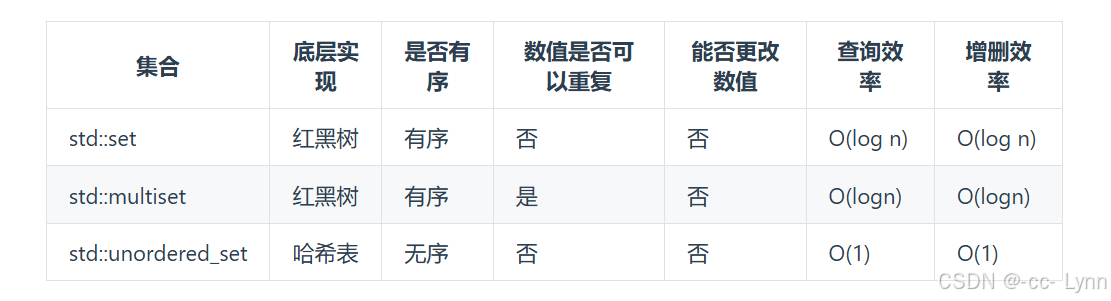
Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。 例如要查询一个名字是否在这所学校里。 要枚举的话时间复杂度是O(n),但如果使用哈希…...
windows实现VNC连接ubuntu22.04服务器
最近弄了一个700块钱的mini主机,刷了ubuntu22.04系统,然后想要在笔记本上通过VNC连接,这样就有了一个linux的开发环境。最后实现的过程为: 安装vnc服务器 安装 VNC 服务器软件: sudo apt update sudo apt install t…...

中国电信星辰大模型:软件工厂与文生视频技术的深度解析
在科技日新月异的今天,人工智能(AI)技术正以惊人的速度改变着我们的生活和工作方式。作为这一领域的领军企业之一,中国电信凭借其强大的研发实力和深厚的技术积累,推出了星辰大模型,旨在为用户带来更加智能、高效、便捷的服务体验。本文将重点介绍中国电信星辰大模型中的…...

项目实战:基于Vue3实现一个小相册
相册的示例效果图 注意看注释... 要实现图片的相册效果,图片命名可以像{img1.jpg,img2.jpg,img3.jpg}类似于这种的命名方式。 CSS部分: <style>/* 伪元素选择器,用于在具有clear_ele类的元素内部的末尾添加一个新的元素 */.clear_ele:…...

macOS安装nvm node
macOS安装nvm macOS安装nvm创建 nvm 工作目录配置环境变量使用 nvm查看可用的 Node.js 版本安装特定版本 macOS安装nvm brew install nvm创建 nvm 工作目录 mkdir ~/.nvm配置环境变量 vim ~/.zshrc# nvm export NVM_DIR"$HOME/.nvm" [ -s "/opt/homebrew/opt…...

解决整合Django与Jinja2兼容性的问题
提问 解决整合Django与Jinja2时遇到了一些兼容性问题。已经按照常规步骤在我的settings.py中配置了Jinja2作为模板引擎,同时保留了Django默认的模板设置。然而尝试同时使用Django和Jinja2时,系统报错提示我没有指定模板。如果我尝试移除Django的默认模板…...

Elasticsearch面试内容整理-高级特性
Elasticsearch 提供了一系列高级特性,这些特性可以极大地增强其搜索、分析和管理能力,使得它在大数据场景中表现出色。以下是 Elasticsearch 的一些重要高级特性: 近实时搜索(Near Real-Time Search) Elasticsearch 的一个关键特性是 近实时搜索(NRT),这意味着数据写入…...

linux通过手工删除文件卸载oracle 11g rac的具体步骤
在linux操作系统中,有些时候我们自己学习和测试会临时搭建的oracle rac。事情完成后,我们想回收资源,需要去卸载oracle rac。为了快速卸载oracle rac,今天我们介绍下如何通过手工删除文件的方式来完成工作(操作都需要在…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
