学习日记_20241123_聚类方法(高斯混合模型)续
前言
提醒:
文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。
其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展及意见建议,欢迎评论区讨论交流。
文章目录
- 前言
- 续:
- 手动实现
- 代码分析
- def __init__(self, n_components, max_iter=100, tol=1e-6)
- def initialize_parameters(self, X)
- def e_step(self, X)
- def m_step(self, X)
- 数学背景
- fit(self, X)
- predict(self, X)
续:
学习日记_20241117_聚类方法(高斯混合模型)
手动实现
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normalclass GaussianMixtureModel:def __init__(self, n_components, max_iter=100, tol=1e-6):self.n_components = n_componentsself.max_iter = max_iterself.tol = toldef initialize_parameters(self, X):n_samples, n_features = X.shapeself.weights = np.ones(self.n_components) / self.n_componentsself.means = X[np.random.choice(n_samples, self.n_components, replace=False)]self.covariances = np.array([np.cov(X, rowvar=False)] * self.n_components)def e_step(self, X):n_samples = X.shape[0]self.responsibilities = np.zeros((n_samples, self.n_components))for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])self.responsibilities[:, k] = self.weights[k] * pdf.pdf(X)self.responsibilities /= self.responsibilities.sum(axis=1, keepdims=True)def m_step(self, X):n_samples, n_features = X.shapeeffective_n = self.responsibilities.sum(axis=0)self.means = np.dot(self.responsibilities.T, X) / effective_n[:, np.newaxis]self.covariances = np.zeros((self.n_components, n_features, n_features))for k in range(self.n_components):X_centered = X - self.means[k]self.covariances[k] = (self.responsibilities[:, k][:, np.newaxis] * X_centered).T @ X_centeredself.covariances[k] /= effective_n[k]self.weights = effective_n / n_samplesdef fit(self, X):self.initialize_parameters(X)log_likelihood_old = 0for iteration in range(self.max_iter):self.e_step(X)self.m_step(X)log_likelihood = 0for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])log_likelihood += np.sum(self.responsibilities[:, k] * np.log(self.weights[k] * pdf.pdf(X) + 1e-10))if np.abs(log_likelihood - log_likelihood_old) < self.tol:print(f"Converged at iteration {iteration}")breaklog_likelihood_old = log_likelihooddef predict(self, X):n_samples = X.shape[0]likelihoods = np.zeros((n_samples, self.n_components))for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])likelihoods[:, k] = self.weights[k] * pdf.pdf(X)return np.argmax(likelihoods, axis=1)# 可视化结果
def plot_results(X, labels, means, covariances):plt.figure(figsize=(8, 6))unique_labels = np.unique(labels)colors = ['r', 'g', 'b', 'c', 'm', 'y']for i, label in enumerate(unique_labels):plt.scatter(X[labels == label, 0], X[labels == label, 1], s=20, color=colors[i % len(colors)], label=f"Cluster {label + 1}")# 绘制高斯分布的等高线mean = means[label]cov = covariances[label]x, y = np.meshgrid(np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 100),np.linspace(X[:, 1].min() - 1, X[:, 1].max() + 1, 100))pos = np.dstack((x, y))rv = multivariate_normal(mean, cov)plt.contour(x, y, rv.pdf(pos), levels=5, colors=colors[i % len(colors)], alpha=0.5)plt.title("Gaussian Mixture Model Clustering")plt.xlabel("Feature 1")plt.ylabel("Feature 2")plt.legend()plt.show()# 测试
if __name__ == "__main__":np.random.seed(42)X1 = np.random.normal(0, 1, (100, 2))X2 = np.random.normal(5, 1, (100, 2))X3 = np.random.normal(10, 1, (100, 2))X = np.vstack((X1, X2, X3))plt.scatter(X[:, 0], X[:, 1])plt.title("Original Data")plt.xlabel("Feature 1")plt.ylabel("Feature 2")gmm = GaussianMixtureModel(n_components=3)gmm.fit(X)labels = gmm.predict(X)plot_results(X, labels, gmm.means, gmm.covariances)
数据与结果为:

代码分析
def init(self, n_components, max_iter=100, tol=1e-6)
class GaussianMixtureModel:def __init__(self, n_components, max_iter=100, tol=1e-6):self.n_components = n_components self.max_iter = max_iter self.tol = tol
n_components:高斯混合模型中的组件数,即聚类的数量。max_iter:最大迭代次数,防止算法不收敛时无限循环。tol:收敛的容忍度,用于判断算法是否收敛。
def initialize_parameters(self, X)
def initialize_parameters(self, X):n_samples, n_features = X.shapeself.weights = np.ones(self.n_components) / self.n_componentsself.means = X[np.random.choice(n_samples, self.n_components, replace=False)]self.covariances = np.array([np.cov(X, rowvar=False)] * self.n_components)
self.weights = np.ones(self.n_components) / self.n_components
设 K K K 为高斯混合模型中的组件数(即n_components)则每个组件的初始权重 π k \pi_k πk 为: π k = 1 K \pi_k = \frac{1}{K} πk=K1,其中 k k k 的取值范围是 1 1 1 到 K K K。self.weights为一个长度为n_components的数组:
π 1 = π 2 = ⋯ = π K = 1 K \pi_1 = \pi_2 = \cdots = \pi_K = \frac{1}{K} π1=π2=⋯=πK=K1
self.means = X[np.random.choice(n_samples, self.n_components, replace=False)]
设 X X X 为数据集,其中包含 n n n 个样本(即n_samples),每个样本是一个特征向量。设 K K K 为高斯混合模型中的组件数(即n_components)。
从数据集 X X X 中随机选择 K K K 个不重复的样本作为初始均值向量。用数学表达式表示就是:
μ k = X i k \mu_k = X_{i_k} μk=Xik
其中:
- μ k \mu_k μk 是第 k k k 个组件的初始均值向量。
- X i k X_{i_k} Xik 是数据集 X X X 中的第 i k i_k ik 个样本。
- i k i_k ik 是从集合 { 1 , 2 , … , n } \{1, 2, \ldots, n\} {1,2,…,n} 中随机选择的不重复的 K K K 个整数。
具体地,可以表示为:
μ 1 , μ 2 , … , μ K = X i 1 , X i 2 , … , X i K \mu_1, \mu_2, \ldots, \mu_K = X_{i_1}, X_{i_2}, \ldots, X_{i_K} μ1,μ2,…,μK=Xi1,Xi2,…,XiK
其中 { i 1 , i 2 , … , i K } \{i_1, i_2, \ldots, i_K\} {i1,i2,…,iK} 是从 { 1 , 2 , … , n } \{1, 2, \ldots, n\} {1,2,…,n} 中随机选择的不重复的 K K K 个整数。
在代码中,np.random.choice(n_samples, self.n_components, replace=False)实现了从 n n n 个样本中随机选择 K K K 个不重复的样本索>引,然后通过这些索引从数据集 X X X 中提取相应的样本作为初始均值向量。
self.covariances = np.array([np.cov(X, rowvar=False)] * self.n_components)
这行代码的目的是初始化高斯混合模型(Gaussian Mixture Model,GMM)中每个组件的协方差矩阵。让我们逐步分析这行代码:
np.cov(X, rowvar=False): 这个函数计算输入数据X的协方差矩阵。参数rowvar=False表示每一列代表一个变量,而每一行代表一个观测值。这是在多维数据中常见的设置,其中每一维(或特征)存储在单独的列中。[np.cov(X, rowvar=False)] * self.n_components: 这部分代码创建了一个列表,其中包含self.n_components个相同的协方差矩阵。self.n_components是GMM中的组件数。np.array(...): 最后,这个列表被转换成一个NumPy数组,使得self.covariances成为一个二维数组,其中每个元素都是一个协方差矩阵。
def e_step(self, X)
def e_step(self, X):n_samples = X.shape[0]self.responsibilities = np.zeros((n_samples, self.n_components))for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])self.responsibilities[:, k] = self.weights[k] * pdf.pdf(X)self.responsibilities /= self.responsibilities.sum(axis=1, keepdims=True)
self.responsibilities = np.zeros((n_samples, self.n_components))
这行代码在高斯混合模型(Gaussian Mixture Model, GMM)中用于初始化一个责任矩阵(responsibility matrix)。
(n_samples, self.n_components)指定了数组的形状,其中n_samples是输入数据集中样本的数量,self.n_components是模型中高斯成分的数量。- 责任矩阵
self.responsibilities的每一行对应于一个样本,而每一列对应于一个高斯成分。- 矩阵中的每个元素
self.responsibilities[i, j]表示样本i属于高斯成分j的责任值(即概率)。它衡量了样本i在当前模型参数下属于成分j的可能性。
这段代码是高斯混合模型(Gaussian Mixture Model, GMM)中 E 步骤(Expectation Step)的一部分。它的主要作用是计算每个样本属于每个高斯成分的责任值(responsibility),并进行归一化处理。我们来逐行分析这段代码的含义:
for k in range(self.n_components):这里的循环遍历所有的高斯成分
k,self.n_components是高斯成分的数量。
pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])使用scipy.stats.multivariate_normal
创建一个多元高斯分布对象self.means[k],协方差矩阵为self.covariances[k]。这表示当前成分k的概率密度函数(PDF)。
self.responsibilities[:, k] = self.weights[k] * pdf.pdf(X)
- 这一行计算每个样本在高斯成分
k下的责任值,并将其存储在责任矩阵self.responsibilities的第k列中。self.weights[k]是成分k的混合权重,表示该成分在总体中占的比例。pdf.pdf(X)计算所有输入样本X在成分k下的概率密度值。self.weights[k] * pdf.pdf(X)计算每个样本在成分k下的加权概率密度(即责任值)。
self.responsibilities /= self.responsibilities.sum(axis=1, keepdims=True)
- 这行代码对责任矩阵进行归一化处理,使得每个样本在所有成分上的责任值之和为 1。
self.responsibilities.sum(axis=1, keepdims=True)计算每个样本在所有成分上的总责任值。- 将责任矩阵每一行的值除以该行的总和,确保每个样本的责任值在所有成分之间是一个概率分布。
def m_step(self, X)
def m_step(self, X):n_samples, n_features = X.shapeeffective_n = self.responsibilities.sum(axis=0)self.means = np.dot(self.responsibilities.T, X) / effective_n[:, np.newaxis]self.covariances = np.zeros((self.n_components, n_features, n_features))for k in range(self.n_components):X_centered = X - self.means[k]self.covariances[k] = (self.responsibilities[:, k][:, np.newaxis] * X_centered).T @ X_centeredself.covariances[k] /= effective_n[k]self.weights = effective_n / n_samples
effective_n = self.responsibilities.sum(axis=0)
这行代码的作用是计算每个高斯成分的有效样本数量(effective number of samples),并将其存储在变量effective_n中。我们来详细分析这一行代码的含义。
self.responsibilities:
- 这是之前提到的责任矩阵,形状为
(n_samples, n_components),其中每一行对应一个样本,每一列对应一个高斯成分。矩阵中的每个值表示样本对某个成分的责任。self.responsibilities.sum(axis=0):
sum(axis=0)表示对责任矩阵的列进行求和。- 这将返回一个一维数组,长度等于高斯成分的数量(
n_components)。- 数组中的每个元素
effective_n[k]表示第k个高斯成分的有效样本数量,即所有样本在该成分上的责任值之和。
- 有效样本数量:有效样本数量反映了每个高斯成分在当前模型下的“重要性”或“权重”。如果某个成分的有效样本数量很小,说明这个成分对当前数据的解释能力较弱。
self.means = np.dot(self.responsibilities.T, X) / effective_n[:, np.newaxis]
这行代码用于更新高斯混合模型中每个高斯成分的均值(means)。让我们逐步分析这行代码及其背后的逻辑。
self.responsibilities.T:
self.responsibilities是一个形状为(n_samples, n_components)的矩阵,表示每个样本对每个高斯成分的责任值。self.responsibilities.T是将责任矩阵进行转置,得到一个形状为(n_components, n_samples)的矩阵。np.dot(self.responsibilities.T, X):
X是输入数据矩阵,形状为(n_samples, n_features),表示n_samples个样本的特征。- 执行矩阵乘法
np.dot(self.responsibilities.T, X)将会产生一个形状为(n_components, n_features)的矩阵。- 这里,每一行对应一个高斯成分,表示该成分加权后的特征总和。具体来说,这些特征是根据每个样本在该成分上的责任值加权后的结果。
effective_n[:, np.newaxis]:
effective_n是一个一维数组,表示每个高斯成分的有效样本数量(我们在之前的讨论中提到过)。- 使用
np.newaxis将effective_n转换为形状为(n_components, 1)的列向量,这样可以在后续的除法运算中进行广播。- 最后的除法:
- 将加权特征总和除以每个成分的有效样本数量,得到加权均值。
- 这一步的结果将更新
self.means,即每个高斯成分的新均值。数学背景
在高斯混合模型中,均值的更新可以用以下公式表示:
μ k = ∑ i = 1 N γ i k x i ∑ i = 1 N γ i k \mu_k = \frac{\sum_{i=1}^{N} \gamma_{ik} x_i}{\sum_{i=1}^{N} \gamma_{ik}} μk=∑i=1Nγik∑i=1Nγikxi
其中:
- μ k \mu_k μk是第 k k k个高斯成分的均值。
- γ i k \gamma_{ik} γik是样本 i i i对成分 k k k的责任值。
- x i x_i xi 是样本 i i i的特征向量。
这行代码正是这个公式的实现形式,通过矩阵运算来有效地更新每个成分的均值。
这段代码的目的是为高斯混合模型中的每个高斯成分计算协方差矩阵,并更新权重。
self.covariances = np.zeros((self.n_components, n_features, n_features))
这一行初始化每个高斯成分的协方差矩阵为零矩阵,形状为(n_components, n_features, n_features),即为每个成分分配一个 n features × n features n_{\text{features}} \times n_{\text{features}} nfeatures×nfeatures 的协方差矩阵。for k in range(self.n_components):
这个循环遍历每一个高斯成分,从 0 到self.n_components - 1。X_centered = X - self.means[k]
这行代码计算每个样本相对于当前成分均值的偏差。X_centered是一个包含所有样本的矩阵,其中每个样本的特征值都减去了该成分的均值。self.covariances[k] = (self.responsibilities[:, k][:, np.newaxis] * X_centered).T @ X_centered
这里计算协方差矩阵的主要部分:
self.responsibilities[:, k][:, np.newaxis]:提取第 k k k 个成分的责任值,并将其转换为列向量。* X_centered:将责任值与居中后的数据相乘,以加权样本。(.T @ X_centered):进行矩阵乘法,计算加权样本的外积,从而得到一个 n features × n features n_{\text{features}} \times n_{\text{features}} nfeatures×nfeatures 的矩阵。- 协方差计算
- 计算得到的结果表示了当前成分的加权协方差矩阵,但为了得到正确的协方差矩阵,还需要将其除以该成分的有效样本数量。
self.covariances[k] /= effective_n[k]
- 将加权结果除以
effective_n[k],得到第 k k k 个高斯成分的协方差矩阵。
- 权重更新
self.weights = effective_n / n_samples
- 最后一行代码用于计算每个高斯成分的权重。权重的计算是将每个成分的有效样本数量除以总样本数量
n_samples,从而得到每个成分在整个模型中的比重。
fit(self, X)
def fit(self, X):self.initialize_parameters(X)log_likelihood_old = 0for iteration in range(self.max_iter):self.e_step(X)self.m_step(X)log_likelihood = 0for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])log_likelihood += np.sum(self.responsibilities[:, k] * np.log(self.weights[k] * pdf.pdf(X) + 1e-10))if np.abs(log_likelihood - log_likelihood_old) < self.tol:print(f"Converged at iteration {iteration}")breaklog_likelihood_old = log_likelihood
这段代码实现了高斯混合模型(GMM)中的
fit方法。它通过期望最大化(EM)算法来拟合模型,计算对数似然(log likelihood)。
- 初始化参数:
Initialize μ k , Σ k , and π k for all components k \text{Initialize } \mu_k, \Sigma_k, \text{ and } \pi_k \text{ for all components } k Initialize μk,Σk, and πk for all components k- E步(期望步):
在E步中,计算每个数据点对每个成分的责任(即每个组件生成该数据点的概率):
r n k = π k ⋅ N ( x n ∣ μ k , Σ k ) ∑ j = 1 K π j ⋅ N ( x n ∣ μ j , Σ j ) r_{nk} = \frac{\pi_k \cdot \mathcal{N}(x_n | \mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \cdot \mathcal{N}(x_n | \mu_j, \Sigma_j)} rnk=∑j=1Kπj⋅N(xn∣μj,Σj)πk⋅N(xn∣μk,Σk)
其中, r n k r_{nk} rnk 是数据点 x n x_n xn 对于成分 k k k 的责任值, N ( x n ∣ μ k , Σ k ) \mathcal{N}(x_n | \mu_k, \Sigma_k) N(xn∣μk,Σk) 是多元正态分布的概率密度函数。- M步(最大化步):
在M步中,更新模型参数,即均值、协方差和权重:
- 更新均值:
μ k = 1 N k ∑ n = 1 N r n k x n \mu_k = \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} x_n μk=Nk1n=1∑Nrnkxn- 更新协方差:
Σ k = 1 N k ∑ n = 1 N r n k ( x n − μ k ) ( x n − μ k ) T \Sigma_k = \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (x_n - \mu_k)(x_n - \mu_k)^T Σk=Nk1n=1∑Nrnk(xn−μk)(xn−μk)T- 更新权重:
π k = N k N \pi_k = \frac{N_k}{N} πk=NNk
其中, N k = ∑ n = 1 N r n k N_k = \sum_{n=1}^{N} r_{nk} Nk=∑n=1Nrnk 是属于成分 k k k 的有效样本数量。
- 对数似然计算:
对数似然是整个数据集 X X X 在模型下的对数概率:
log L = ∑ n = 1 N log ( ∑ k = 1 K π k ⋅ N ( x n ∣ μ k , Σ k ) ) \log L = \sum_{n=1}^{N} \log \left( \sum_{k=1}^{K} \pi_k \cdot \mathcal{N}(x_n | \mu_k, \Sigma_k) \right) logL=n=1∑Nlog(k=1∑Kπk⋅N(xn∣μk,Σk))
由于在计算中添加了一个小的常数 1 e − 10 1e-10 1e−10 以避免对数计算中的数值问题,完整的表达式为:
log L ≈ ∑ n = 1 N ∑ k = 1 K r n k log ( π k ⋅ N ( x n ∣ μ k , Σ k ) + 1 e − 10 ) \log L \approx \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \log \left( \pi_k \cdot \mathcal{N}(x_n | \mu_k, \Sigma_k) + 1e-10 \right) logL≈n=1∑Nk=1∑Krnklog(πk⋅N(xn∣μk,Σk)+1e−10)- 收敛检查:
收敛条件是检查当前对数似然与上一轮的对数似然之差是否小于容忍度 tol \text{tol} tol:
∣ log L − log L old ∣ < tol |\log L - \log L_{\text{old}}| < \text{tol} ∣logL−logLold∣<tol
predict(self, X)
def predict(self, X):n_samples = X.shape[0]likelihoods = np.zeros((n_samples, self.n_components))for k in range(self.n_components):pdf = multivariate_normal(mean=self.means[k], cov=self.covariances[k])likelihoods[:, k] = self.weights[k] * pdf.pdf(X)return np.argmax(likelihoods, axis=1)
这段代码实现了高斯混合模型(GMM)中的
predict方法,目的是根据已拟合的模型来预测给定数据点 X X X 的每个样本属于哪个组件。
- 输入数据:
- X X X 是一个 n × d n \times d n×d 的矩阵,其中 n n n 是样本数量, d d d 是特征维数。
- 初始化似然数组:
- 创建一个 n × K n \times K n×K 的矩阵
likelihoods,其中 K K K 是组件的数量。这个矩阵将用于存储每个样本在每个组件下的似然值。
likelihoods = [ 0 0 … 0 0 0 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … 0 ] ( n × K ) \text{likelihoods} = \begin{bmatrix} 0 & 0 & \ldots & 0 \\ 0 & 0 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 0 \end{bmatrix} \quad (n \times K) likelihoods= 00⋮000⋮0……⋱…00⋮0 (n×K)- 计算每个组件的似然:
- 对于每个组件 k k k,计算数据点 X X X 在该组件下的加权似然值:
likelihoods [ : , k ] = π k ⋅ N ( X ∣ μ k , Σ k ) \text{likelihoods}[:, k] = \pi_k \cdot \mathcal{N}(X | \mu_k, \Sigma_k) likelihoods[:,k]=πk⋅N(X∣μk,Σk)
其中:- π k \pi_k πk 是组件 k k k 的权重(混合系数)。
- N ( X ∣ μ k , Σ k ) \mathcal{N}(X | \mu_k, \Sigma_k) N(X∣μk,Σk) 是多元正态分布在组件 k k k 下的概率密度函数。
- 确定预测标签:
- 对于每个样本,选择具有最大似然值的组件,返回其索引作为预测类别:
predictions = arg max k ( likelihoods [ : , k ] ) \text{predictions} = \arg\max_{k}(\text{likelihoods}[:, k]) predictions=argkmax(likelihoods[:,k])
这意味着,对于每个样本 $ n $,其最终预测标签为:
y ^ n = arg max k ( π k ⋅ N ( x n ∣ μ k , Σ k ) ) \hat{y}_n = \arg\max_{k} \left( \pi_k \cdot \mathcal{N}(x_n | \mu_k, \Sigma_k) \right) y^n=argkmax(πk⋅N(xn∣μk,Σk))- 返回预测结果:
- 结果是一个长度为 n n n 的数组,包含每个样本的预测组件索引。
总结起来,
predict方法通过计算每个样本在每个高斯组件下的加权似然,将样本分配给最可能的组件,从而完成聚类或分类任务。
相关文章:

学习日记_20241123_聚类方法(高斯混合模型)续
前言 提醒: 文章内容为方便作者自己后日复习与查阅而进行的书写与发布,其中引用内容都会使用链接表明出处(如有侵权问题,请及时联系)。 其中内容多为一次书写,缺少检查与订正,如有问题或其他拓展…...

SpringMVC——简介及入门
SpringMVC简介 看到SpringMVC这个名字,我们会发现其中包含Spring,那么SpringMVC和Spring之间有怎样的关系呢? SpringMVC隶属于Spring,是Spring技术中的一部分。 那么SpringMVC是用来做什么的呢? 回想web阶段&#x…...

文件操作完成后,为什么要关闭文件
原因包括: 释放系统资源:打开文件时,操作系统会分配资源,如文件描述符或句柄,用于管理文件访问。如果文件保持打开状态,这些资源就不会被释放,可能导致资源耗尽。 确保数据完整性:写…...

vue3+echarts+ant design vue实现进度环形图
1、代码 <div> <!-- 目标环形图 --><div id"main" class"chart_box"> </div><div class"text_target">目标</div> </div>// 目标环形图 const onEcharts () > {// 基于准备好的dom,初…...

使用argo workflow 实现springboot 项目的CI、CD
文章目录 基础镜像制作基础镜像设置镜像源并安装工具git下载和安装 Maven设置环境变量设置工作目录默认命令最终dockerfile 制作ci argo workflow 模版volumeClaimTemplatestemplatesvolumes完整workflow文件 制作cd argo workflow 模版Workflow 结构Templates 定义创建 Kubern…...
:序列型动态规划)
C++知识点总结(58):序列型动态规划
动态规划Ⅰ 一、基础1. 意义2. 序列 dp 解法 二、例题1. 最大子段和2. 删数最大子段和(数据强度:pro max)3. 最长上升子序列(数据强度:pro max)4. 3 或 5 的倍数序列5. 数码约数序列 一、基础 1. 意义 动…...
使用)
go interface(接口)使用
在 Go 语言中,接口(interface)是一种抽象类型,它定义了一组方法,但是不实现这些方法。接口指定了一个对象的行为,而不关心对象的具体实现。接口使得代码更加灵活和可扩展。 定义接口 接口使用 type 关键字…...

【docker】docker commit 命令 将当前容器的状态保存为一个新的镜像
在Docker容器中安装了许多软件,并希望将当前容器的状态保存为一个新的镜像,可以使用docker commit命令来创建一个新的镜像。以下是如何操作的步骤: 找到容器ID或名称: 首先,需要找到想要保存的容器的ID或名称。可以使用…...

使用 Java 中的 `String.format` 方法格式化字符串
前言 在编程过程中,我们经常需要创建格式化的字符串来满足特定的需求,比如生成用户友好的消息、构建报告或是输出调试信息。Java 提供了一个强大的工具——String.format 方法,它可以帮助我们轻松地完成这些任务。 String.format 方法简介 …...
)
图论最短路(floyed+ford)
Floyd 算法简介 Floyd 算法(也称为 Floyd-Warshall 算法)是一种动态规划算法,用于解决所有节点对之间的最短路径问题。它可以同时处理加权有向图和无向图,包括存在负权边的情况(只要没有负权环)。 核心思…...

BERT的中文问答系统39
实现当用户在GUI中输入问题(例如“刘邦”)且输出的答案被标记为不正确时,自动从百度百科中搜索相关内容并显示在GUI中的功能,我们需要对现有的代码进行一些修改。以下是完整的代码,包括对XihuaChatbotGUI类的修改以及新…...

从 Mac 远程控制 Windows:一站式配置与实践指南20241123
引言:跨平台操作的需求与挑战 随着办公场景的多样化,跨平台操作成为现代开发者和 IT 人员的刚需。从 Mac 系统远程控制 Windows,尤其是在同一局域网下,是一种高效解决方案。不仅能够灵活管理资源,还可以通过命令行简化…...
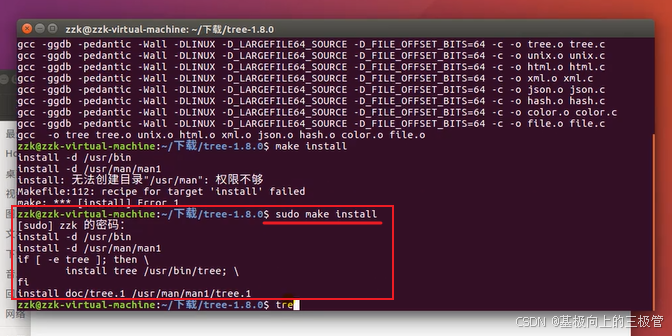
【Linux学习】【Ubuntu入门】1-5 ubuntu软件安装
1.使用sudo apt-get install vim:安装vim编辑器。 参考安装 安装时可能会遇到的问题 2.deb软件安装命令sudo dpkg -i xxx.deb 下载软件安装包时下载Linux版本,在Ubuntu中双击deb文件或者输入命令sudo dpkg -i xxx.deb,xxx.deb为安装包名称…...

如何自动下载和更新冰狐智能辅助?
冰狐智能辅助的版本更新非常快,如果设备多的话每次手工更新会非常麻烦,现在分享一种免费的自动下载和安装冰狐智能辅助的方法。 一、安装迅雷浏览器 安装迅雷浏览器1.19.0.4280版本,浏览器用于打开冰狐的官网,以便于从官网下载a…...

动态渲染页面爬取
我们可以直接使用模拟浏览器运行的方式来实现,这样就可以做到在浏览器中看到是什么样,抓取的源码就是什么样,也就是可见即可爬。这样我们就不用再去管网页内部的 JavaScript 用了什么算法渲染页面,不用管网页后台的 Ajax 接口到底…...

C++适配器模式之可插入适配器的实现模式和方法
可插入适配器与Adaptee的窄接口 在C适配器模式中,可插入适配器(Pluggable Adapter)是指适配器类的设计允许在运行时动态地插入不同的Adaptee对象,从而使适配器具有灵活性和可扩展性。这种设计使得适配器不仅限于适配一个特定的Ad…...
每日一练:【动态规划算法】斐波那契数列模型之第 N 个泰波那契数(easy)
1. 第 N 个泰波那契数(easy) 1. 题目链接:1137. 第 N 个泰波那契数 2. 题目描述 3.题目分析 这题我们要求第n个泰波那契Tn的值,很明显的使用动态规划算法。 4.动态规划算法流程 1. 状态表示: 根据题目的要求及公…...
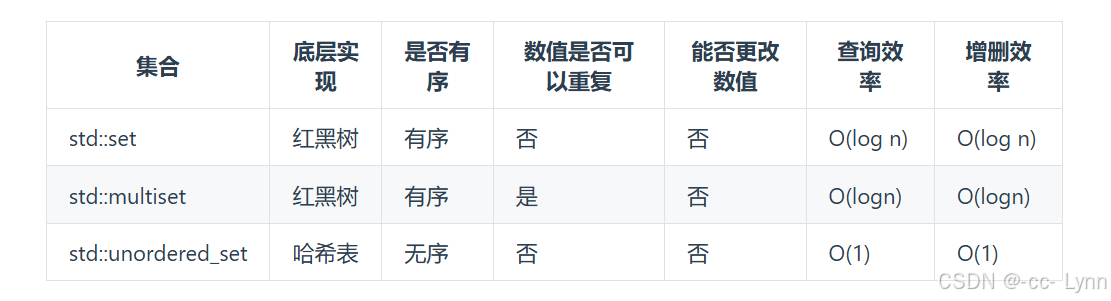
Hash table类算法【leetcode】
哈希表中关键码就是数组的索引下标,然后通过下标直接访问数组中的元素 那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。 例如要查询一个名字是否在这所学校里。 要枚举的话时间复杂度是O(n),但如果使用哈希…...
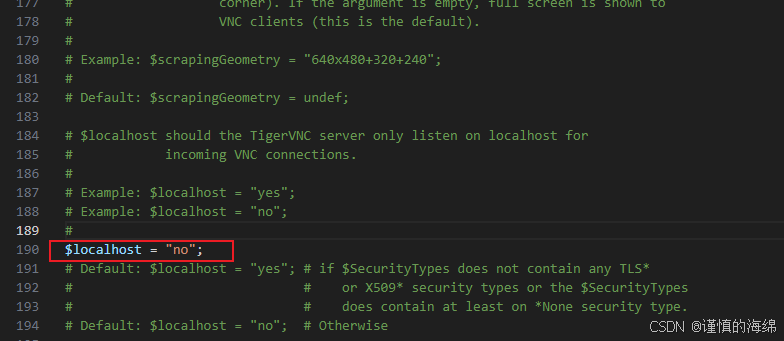
windows实现VNC连接ubuntu22.04服务器
最近弄了一个700块钱的mini主机,刷了ubuntu22.04系统,然后想要在笔记本上通过VNC连接,这样就有了一个linux的开发环境。最后实现的过程为: 安装vnc服务器 安装 VNC 服务器软件: sudo apt update sudo apt install t…...

中国电信星辰大模型:软件工厂与文生视频技术的深度解析
在科技日新月异的今天,人工智能(AI)技术正以惊人的速度改变着我们的生活和工作方式。作为这一领域的领军企业之一,中国电信凭借其强大的研发实力和深厚的技术积累,推出了星辰大模型,旨在为用户带来更加智能、高效、便捷的服务体验。本文将重点介绍中国电信星辰大模型中的…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...



