力扣hot100道【贪心算法后续解题方法心得】(三)
力扣hot100道【贪心算法后续解题方法心得】
- 十四、贪心算法
- 关键解题思路
- 1、买卖股票的最佳时机
- 2、跳跃游戏
- 3、跳跃游戏 | |
- 4、划分字母区间
- 十五、动态规划
- 什么是动态规划?
- 关键解题思路和步骤
- 1、打家劫舍
- 2、01背包问题
- 3、完全平方式
- 4、零钱兑换
- 5、单词拆分
- 6、最长递增子序列
- 7、乘积最大子序列
- 8、分割等和子集
- 十六、多为动态规划
- 1、不同路径
- 2、最小路径和
- 3、最长回文子串
- 4、最长公共子序列
- 5、编辑距离
- 十七、技巧
- 十八、排序算法
- 概述
- 1、冒泡排序(Bubble Sort)
- 2、选择排序(Selection Sort)
- 3、插入排序
- 4、快速排序(Quick Sort)!!!
- 5、归并排序(Merge Sort)
- 6、堆排序(Heap Sort)
- 7、希尔排序(Shell Sort)
- 8、桶排序(Bucket Sort)
- 9、基数排序(Radix Sort)
- 其他相关内容
- 1. 哈希-矩阵解题心得(一):[https://blog.csdn.net/a147775/article/details/143558612](https://blog.csdn.net/a147775/article/details/143558612)
- 2. 链表-堆解题心得(二):[https://blog.csdn.net/a147775/article/details/144218993](https://blog.csdn.net/a147775/article/details/144218993)
十四、贪心算法
关键解题思路
理解贪心的本质是:选择每一阶段的局部最优,从而达到全局最优。
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
1、买卖股票的最佳时机
1)解题关键思路
- 在最低价格买入,最高利润卖出(思路是错误的) 如:[2,100,1,5]可能在最低价格1买入,然后5卖出吗,不可能。
- 总的来说应该是在遍历每一天中后续相邻天数的净利润相加,净利润<0舍弃重新开始得到最大值。
2)代码
public int maxProfit(int[] prices) {int maxSum = 0;int sum = 0;for (int i = 0; i < prices.length; i++) {sum += prices[i];if (sum < 0) sum = 0;maxSum = Math.max(maxSum, sum);}return maxSum;}
3)分析
- 求每一天的净利润相加,得到的就是最大值,<0就直接舍弃从下一个元素开始继续重复上述操作。
2、跳跃游戏
1)解题思路与关键难点
- 就是跳到哪里进行覆盖,如果覆盖是数组长度索引最大,直接可以
关键难点
知道思路是什么,但却写不出代码,不知道应该怎么写代码
解答
- 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
- 贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
1)解题关键思路 - coverRange覆盖达到nums.length-1
- 每次遍历最大遍历只能到达converRange
2)代码
// 思路:求每个下标下的最大覆盖位置public boolean canJump(int[] nums) {if (nums.length ==1) return true;int coverRange = 0;// 为什么是相等?// 因为可以跳到该覆盖索引的下标下for (int i = 0; i <= coverRange; i++) {coverRange = Math.max(coverRange, i + nums[i]);if (coverRange >= nums.length -1) return true;}return false;}
3)分析
- 判断coverRange覆盖达到nums.length-1返回true
- 每次遍历最大遍历只能到达converRange,并在每次更新converRange的最大赋值。
3、跳跃游戏 | |
1)解题关键
要想清楚什么时候步数才一定要加一呢?
关键点:
所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数!
这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖
2)代码
// 尽可能的选择跳最远的public int jump(int[] nums) {if (nums.length == 1) return 0;int nextCoverRange = 0;int currentCover = 0;int res = 0;for (int i = 0; i <= nextCoverRange ; i++) {nextCoverRange = Math.max(nextCoverRange , i + nums[i]);if (nextCoverRange >= nums.length - 1) {res++;break;}// 在当前覆盖范围内寻找最大覆盖范围,// 如果走完当前覆盖范围计算下一步最大的覆盖范围还没有到达终点,// 再加一步进行移动if (i == currentCover) {// 开始跳跃,跳跃范围是nextCoverRange res++;currentCover = nextCoverRange ;}}return res;}
3)分析
- 在当前覆盖索引寻找nextCoverRange 最大值是否覆盖nums.length - 1,如果覆盖直接+1退出,如果遍历结束还没有就进行跳转到下一个nextConverRange中的某个位置继续遍历。
4、划分字母区间
1)关键解题思路
题目要求同一个字母只能出现在一个片段里面,故而解题关键就是找出同一个字母出现的最远的索引即可。
2)代码
public List<Integer> partitionLabels(String s) {// 记录每个字母最后的索引位置int[] last = new int[26];char[] chars = s.toCharArray();// 获取每个字母最后的起始位置for (int i = 0; i < chars.length; i++) {last[chars[i] - 'a'] = i;}List<Integer> list = new ArrayList<>();int end = 0;int start = 0;for (int i = 0; i < chars.length; i++) {// 什么时候加入list?end = Math.max(end, last[i]);if (i == end) {list.add(end - start + 1);start = end + 1;}}return list;}
3)分析
- 最重要一步就是记录同一个字母的最后索引位置,然后遍历等到i == end时候收集一个区间的结果
十五、动态规划
什么是动态规划?
动态规划(Dynamic Programming,简称DP)是一种解决具有重叠子问题和最优子结构特性的问题的方法。其核心思想是将一个复杂的问题分解成一系列更小的子问题,并通过存储这些子问题的解来避免重复计算,从而提高算法效率,即为利用空间存储已经计算过的值,达到空间换时间。
关键解题思路和步骤
思路:
将一个复杂的问题分解成一系列更小的子问题,通过存储这些子问题的解进行后续问题的解,避免重复计算。
步骤:
- 确定dp数组以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
为什么是先进行递推公式的确定再进行初始化呢?
因为一些情况是递推公式决定了dp数组要如何初始化!
1、打家劫舍
1)解题关键
- 确定dp数组含义
- 根据第i家偷还是不偷,确定递推公式,如果偷:dp[i] = dp[i-2] + num[i],不偷就是:dp[i] = dp[i-1],因为是求最大,故而递推公式为:dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
- 初始化,根据递推公式可知,dp[0] = 0,dp[1] = nums[0]必偷。
- 确定遍历顺序,从0开始偷进行计算。
2)代码
public int rob(int[] nums) {int length = nums.length;if ( length == 0) return 0;int[] dp = new int[length + 1];dp[0] = 0;dp[1] = nums[0];for (int i = 2; i <= length; i++) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i-1]);}return dp[length];}
3)分析同1)
2、01背包问题
1)解题关键
2)关键优化代码
// 外层循环遍历每个类型的研究材料for (int i = 0; i < M; i++) {// 内层循环从 N 空间逐渐减少到当前研究材料所占空间for (int j = N; j >= costs[i]; j--) {// 考虑当前研究材料选择和不选择的情况,选择最大值dp[j] = Math.max(dp[j], dp[j - costs[i]] + values[i]);}}
3)分析
- 确定遍历顺序,背包遍历顺序为倒叙,防止同一个物品被添加多次。
3、完全平方式
1)解题关键
- 动态规划5个步骤,并类比完全背包和01背包解法。
- 无非就是1,4,9这些是物品重量,然后n是背包容量,可以重复添加,求最小次数加满背包。
- 遍历顺序就是先遍历物品再遍历背包
- 类比完全背包问题
2)代码
public int numSquares(int n) {// 把平方当作物品(无限使用),然后n代表背包容量// 刚好装满这个背包最少需要多少个物品// dp[i]表示装满容量为i的背包最少需要多少个物品int[] dp = new int[n + 1];// 因为求的是min,防止递推公式的值被初始值覆盖Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;dp[1] = 1;for (int i = 1; i*i <= n; i++) { //遍历物品for (int j = i*i; j <= n; j++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
3)分析
- 完全背包问题,无非就是一个物品可以重复添加达到背包被装满为止的最大值。
4、零钱兑换
解法同上面一样
5、单词拆分
1)关键解题思路

dp[i]:表示i长度的字符串能否被若干个单词组成。故而推导公式 dp[j] && wordDictSet.contains(s.substring(j, i))
-> dp[i] = true
2)代码
// 典型背包问题 把wordDict当作物品即可public boolean wordBreak(String s, List<String> wordDict) {Set<String> wordDictSet = new HashSet(wordDict);int sLength = s.length();// 代表容量背包的最大值boolean[] dp = new boolean[sLength + 1];dp[0] = true;for (int i = 1; i <= s.length(); i++) {for (int j = 0; j < i; j++) {if (dp[j] && wordDictSet.contains(s.substring(j, i))) {dp[i] = true;}}}return dp[sLength];}
6、最长递增子序列
1)关键解题步骤
dp[i]:含义代表的是对应的索引下标的最长递增子序列。
2)代码
public int lengthOfLIS(int[] nums) {// 以nums[i]为结尾的最长递增子序列int[] dp = new int[nums.length];// 最低要求都是1Arrays.fill(dp, 1);int res = 1;for (int i = 0; i < nums.length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}res = Math.max(res, dp[i]);}// 结果不一定是对应的结尾可能是之前的return res;}
3)分析
如果nums[i] > nums[j],代表有一个索引下标符合条件,不断遍历寻找最大值。有点类似单词拆分题目的解法
7、乘积最大子序列
1)解题关键
定义两个变量 iMax 和 iMin分别用于记录[0,i)为止的最大乘积和最小乘积。这是因为负数乘以最大值可能会变成最小值,而负数乘以最小值可能会变成最大值。同时,还需要一个变量 max来记录全局的最大乘积。
2)代码
public int maxProduct(int[] nums) {// 设置最大值为初始值int max = Integer.MIN_VALUE,imax = 1, imin = 1;for (int i = 0; i < nums.length; i++) {if (nums[i] < 0) {int temp = imax;imax = imin;imin = temp;}imax = Math.max(imax * nums[i], nums[i]);imin = Math.min(imin * nums[i], nums[i]);max = Math.max(imax, max);}return max;}
8、分割等和子集
1)关键解题思路
- 求相同的等和,故而进行累加sum,判断sum % 2 != 0 。
- target = sum / 2,此时可以看作是背包容量,数组里面的元素就是物品,无非就是从添加物品能否填满背包。
2)代码
public boolean canPartition(int[] nums) {int sum = 0;int n = nums.length;for (int i = 0; i < n; i++) {sum += nums[i];}if (sum % 2 != 0) return false;int target = sum / 2;int[] dp = new int[target + 1];dp[0] = 0;for (int i = 1; i < n; i++) {for (int j = target; j >=nums[i] ; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return target == dp[target];}
十六、多为动态规划
1、不同路径
1)解题思路
某一个网格的路径 = 左边网格右走一步 + 上边网格下走一步。
定义 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
2)代码
//2.空间优化public int uniquePaths(int m, int n) {// dp[i][j]表示到达(i,j)的路径数int[] dp = new int[n];for (int i = 0; i < n; i++) {dp[i] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {// dp[j]的表示当前这一行 的dp[j] dp[j-1]表示上一行的dp[j]dp[j] = dp[j] + dp[j - 1];}}return dp[n - 1];// 初始化第一列}}
2、最小路径和
1)关键解题思路
某网格最小值无非就是公式: // grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j] ;
通过累加改变每个网格的值,此时网格的值代表所有路径下最小的和,也就是直接在grid[i][j] 上面直接修改。
2)代码
public int minPathSum(int[][] grid) {// grid[i][j] = min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j] ;// 原 grid 矩阵元素中被覆盖为 dp 元素后(都处于当前遍历点的左上方),不会再被使用到for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[0].length; j++) {if (i == 0 && j == 0) continue;else if (i == 0) grid[i][j] += grid[i][j - 1];else if ((j == 0)) grid[i][j] += grid[i - 1][j];else grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);}}return grid[grid.length - 1][grid[0].length - 1];}
3、最长回文子串
1)解题关键思路
解题关键方法:中心扩散法
如何理解中心扩散法?
它的基本思想是从每一个可能的“中心”开始,向两边扩展,直到不能再扩展为止。
即为从每一个位置出发,向两边扩散。遇到不是回文时候就直接结束。
例如:“babad”
第二个b位置:2,出发最长回文子串为多少。怎么找?
- 先往左寻找与当期位置相同的字符,直到不相等。
- 往右寻找与当前位置相同的字符,直到不相等
- 最后就进行左右双向扩散,直到左和右不相等。
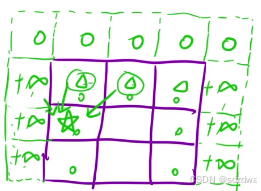
如图所示

每个位置向两边扩散都会出现一个窗口大小(len)。如果 len>maxLen(用来表示最长回文串的长度)。则更新 maxLen 的值。
因为我们最后要返回的是具体子串,而不是长度,因此,还需要记录一下 maxLen 时的起始位置(maxStart),即此时还要 maxStart=len。
2)代码
public String longestPalindrome(String s) {int length = s.length();if (length == 1) return s;// 定义中心扩散中心的左右边界int left = 0;int right = 0;// 当前中心点的回文字串最大长度int len = 1;// 某结果中心点的最大回文字串的起始索引int maxStart = 0;// 该结果最大的回文字串长度int maxLen = 0;for (int i = 0; i < length; i++) {// 先进行左右扩散left = i-1;right = i+1;// 左扩散while (left >= 0 && s.charAt(left) == s.charAt(i)) {left--;len++;}// 右扩散while (right < length && s.charAt(right) == s.charAt(i)) {right++;len++;}// 左右扩散while (right < length && left >= 0 && s.charAt(right) == s.charAt(left)) {left--;right++;len += 2;}// 最终得到以该i位置为中心的回文字串长度if (len > maxLen) {maxLen = len;// 记录起始位置maxStart = left+1;}// 重置len 为下一个准备len = 1;}return s.substring(maxStart, maxStart + maxLen);}
3)分析
- 最为关键的一点就是 : left = i-1;right = i+1;先提前扩散好,为后续左,右,左右扩散s.charAt(left) == s.charAt(i)等比较做好准备。
- 因为提前左右扩散,所以最终的left是不符合的,而left+1才是回文子串的起始位置。
4、最长公共子序列
1)解题关键
- 求公共最长子序列,就是利用dp数组存放之前已经计算过的值依次计算到text1,text2结尾得出结果。
- 利用二维数组dp[i][j] 表示【0 - t1-1】区间和【0 - t2-1】区间的最长公共子序列,依次存储计算过的值,最终得到结果:dp[t1][t2];
2)代码
public int longestCommonSubsequence(String text1, String text2) {int t1 = text1.length();int t2 = text2.length();// 代表0 - t1-1和0 - t2-1的最长公共子序列int[][] dp = new int[t1 + 1][t2 + 1];for (int i = 1; i <= t1; i++) {for (int j = 1; j <= t2; j++) {if (text1.charAt(i - 1) == text2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;}else{dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[t1][t2];}
3)分析
- 当两个text1.charAt(i - 1) == text2.charAt(j - 1)代表的是最后一个字母相等,此时+1,当不相等时候,等于text1-1和text2或者text1和text2-1比较得到结果。
5、编辑距离
1)解题关键
本题咋一看完全没有思路,其实解决本题的思路主要就是定义二维的动态dp,并理解dp[i][j]:[0,i-1] [0,j-1]区间的最少操作数,思路其实和上一题最长公共子序列长度差不多,无非就是相等时候不用操作,不相等时候进行增删改。
2)代码
public int minDistance(String word1, String word2) {int w1 = word1.length();int w2 = word2.length();char[] W1 = word1.toCharArray();char[] W2 = word2.toCharArray();// dp[i][j]:word1[0..i-1]和word2[0..j-1]的最小编辑距离int[][] dp = new int[w1 + 1][w2 + 1];// 初始化// 初始化for (int i = 0; i <= w1; i++) {dp[i][0] = i;} for (int j = 0; j <= w2; j++) {dp[0][j] = j;}for (int i = 1; i <= w1; i++) {for (int j = 1; j <= w2; j++) {// 相等 等于之前if (W1[i - 1] == W2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];} else {// dp[i - 1][j]:word1删除一个元素,那么就是以下标i - 2为结尾的word1与j-1为结尾的word2的最近编辑距离 再加上一个操作。dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1]) ) + 1;}}}return dp[w1][w2];}
3)分析
无非就是理解递推公式,相等时候:不需要操作直接得出结果dp[i][j] = dp[i - 1][j - 1];
不相等时候: dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1]) ) + 1;对i索引-1操作或者j-1索引操作,最后替换 i-1,j-1操作,求三个操作最小值。
十七、技巧
十八、排序算法
概述
1、冒泡排序(Bubble Sort)
冒泡排序(Bubble Sort):通过重复遍历要排序的列表,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
1)关键解题思路
2)代码
/* 冒泡排序 */void bubbleSort(int[] nums) {int length = nums.length;if(length<2) return;// 只需要遍历length -1遍即可for (int i = length -1 ; i >0 ; i--) {boolean flag = false;for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {int temp = nums[j];nums[j] = nums[j+1];nums[j + 1] = temp;// 每次交换都表示有flag = true;}}// 说明没有进行交换 已经达到有序直接退出if (!flag) break;}}
3)分析
1、时间复杂度
最好情况o(n),最坏情况o(n*n)
2、空间复杂度
o(1)
2、选择排序(Selection Sort)
选择排序(Selection Sort):在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
1)关键解题思路
2)代码
/* 选择排序 */void selectionSort(int[] nums) {int length = nums.length;if(length<2) return;// 只需要遍历length -1遍即可for (int i = 0; i < length-1; i++) {int minIndex = i;for (int j = i; j < length; j++) {if (nums[minIndex] > nums[j]) {// 如果直接这样是无法记录最小值所在的索引位置的minIndex = j;}}int temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;}// 说明没有进行交换 已经达到有序直接退出}
3)分析
1、时间复杂度
o(n*n)
2、空间复杂度
o(1)
3、插入排序
插入排序(Insertion Sort):在已有的有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
1)关键解题思路
2)代码
/* 插入排序 */void insertionSort(int[] nums) {int length = nums.length;if(length<2) return;// 为什么从索引1开始,类似打牌一样,摸到的第一张牌不需要进行排序for (int i = 1; i < length; i++) {// 待排序元素int base = nums[i];// 待排序的有序最后的区间int j = i - 1;// 内循环:将 temp从后向前扫描插入到已排序区间 [0, i-1] 中的正确位置while (j >= 0 && base < nums[j]) {// 将元素向后面移动nums[j + 1] = nums[j];j--;}// 退出循环,此时j是刚好比bse小的 找到插入的索引位置,将其插入nums[j + 1] = base;}}
3)分析
1、时间复杂度
- 最佳情况为o(n)最坏情况o(n*n)
2、空间复杂度
o(1)
3、理解关键解题思路
在已排序序列中从后向前扫描,找到相应位置并插入。
4、快速排序(Quick Sort)!!!
快速排序(Quick Sort):也是基于分治法的排序算法,通过一个“基准数”(pivot)将数组分成两部分,左边部分的所有元素都小于基准数,右边部分的所有元素都大于基准数,然后递归地对这两部分进行排序。
1)解题关键思路
选定一个基准数,大于基准数的就排在右边,小于基准数的就排在左边,重复操作
2)代码
/* 快速排序 */void quickSort(int[] nums, int left, int right) {if (left >= right) return;int baseIndex = partition(nums, left, right);quickSort(nums,left,baseIndex-1);quickSort(nums,baseIndex+1,right);}int partition(int[] nums, int left, int right) {// 选取第一个元素作为基准int base = nums[left];while (left < right) {while (left < right && nums[right] >= base) {right--;}// 进行左右交换// 将较小的元素放到左边nums[left] = nums[right];while (left < right && nums[left] <= base) {left++;}// 将较大的元素放到右边nums[right] = nums[left];}// 最后将基准元素放到正确的位置nums[left] = base;return left;}
3)分析
- 选取一个以左边为基准的元素,然后right来移动寻找小于base的数字,然后放到左边 :nums[left] = nums[right];
- 接下来就是同理可得
1、时间复杂度为 (nlogn)
2、空间复杂度为o(n)
5、归并排序(Merge Sort)
归并排序(Merge Sort):采用分治法的一个典型应用,将已经有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
1)关键解题思路

- 划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
- 合并阶段:当子数组长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束。
2)代码
/* 归并排序 */void mergeSort(int[] nums, int left, int right) {// 终止条件if (left >= right) return;// 递归进行划分阶段int mid = (left + right) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);// 合并左右子数组// 左子数组区间为 [left, mid],// 右子数组区间为 [mid+1, right]merge(nums, left, mid, right);}private void merge(int[] nums, int left, int mid, int right) {int[] temp = new int[right - left + 1];// 左数组起始索引int i = left;// 右数组起始索引int j = mid + 1;int k = 0;// 开始进行左右子数组排序while (i <= mid && j <= right) {if (nums[i] <= nums[j]) {temp[k++] = nums[i];}else{temp[k++] = nums[j];}}// 最后将剩余的元素复制到临时数组中while (i<=mid){temp[k++] = nums[i++];}while (j<=right){temp[k++] = nums[j++];}// 将临时数组temp元素复制回来到原来区间for (int l = 0; k < temp.length; l++) {nums[left + l] = temp[l];}}
3)分析
- 主要就是对数组进行不断mid分为左右子数组,然后再进行合并
- 合并阶段主要就是对左右子数组进行合并。
1、时间复杂度
o(nlogn)
2、空间复杂度
o(n)
6、堆排序(Heap Sort)
堆排序(Heap Sort):利用堆这种数据结构设计的一种排序算法,首先将待排序的数组构建成大顶堆或小顶堆,然后将堆顶元素与末尾元素交换,再重新调整堆,直到排序完成。
1)解题关键
2)代码
/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(int[] nums, int n, int i) {while (true) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = 2 * i + 1;int r = 2 * i + 2;int ma = i;if (l < n && nums[l] > nums[ma])ma = l;if (r < n && nums[r] > nums[ma])ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i)break;// 交换两节点int temp = nums[i];nums[i] = nums[ma];nums[ma] = temp;// 循环向下堆化i = ma;}
}/* 堆排序 */
void heapSort(int[] nums) {// 建堆操作:堆化除叶节点以外的其他所有节点for (int i = nums.length / 2 - 1; i >= 0; i--) {// 进行节点调整siftDown(nums, nums.length, i);}// 从堆中提取最大元素,循环 n-1 轮for (int i = nums.length - 1; i > 0; i--) {// 交换根节点与最右叶节点(交换首元素与尾元素)int tmp = nums[0];nums[0] = nums[i];nums[i] = tmp;// 以根节点为起点 调整剩余部分重新形成大顶堆// siftDown 操作的目的是调整堆中某个节点,使其成为一个有效的堆 // 以为0的值改变了,所以进行0节点调整成堆siftDown(nums, i, 0);}
}
7、希尔排序(Shell Sort)
希尔排序(Shell Sort):是插入排序的一种更高效的改进版本,也称缩小增量排序,通过将原始列表分割成多个子列表分别进行插入排序来提高效率。
1)关键解题思路
理解分组的含义,以及插入排序的关键解题
2)代码
public static void shellSort(int[] nums) {int length = nums.length;if(length<2) return;// 进行分组for (int gap = length / 2; gap >= 1; gap /= 2) {// 对每个分组后的子序列进行插入排序for (int i = gap ; i < length; i++) {int temp = nums[i];int j = i - gap;while (j >= 0 && nums[j] > temp) {nums[j + gap] = nums[j];j -= gap;}nums[j + gap] = temp;}}}
3)分析
1、时间复杂度
- 最佳情况为:O(n log n) 最坏情况O(n^(3/2))
2、空间复杂度
o(1)
3、理解关键解题思路
在已排序序列中从后向前扫描,找到相应位置并插入。
8、桶排序(Bucket Sort)
桶排序(Bucket Sort):工作原理是将数组分到有限数量的桶里。每个桶再分别排序(有可能再使用别的排序算法或是递归使用桶排序)。
1)关键解题思路

将对应的元素放到对应的桶上面去,然后进行在每个桶进行排序。
2)代码
/* 桶排序 */void bucketSort(float[] nums) {// 初始化 k = n/2个桶,预期向每个桶分配2个元素int k = nums.length / 2;List<List<Float>> buckets = new ArrayList<>();// 初始化桶for (int i = 0; i < k; i++) {buckets.add(new ArrayList<>());}for (float num : nums) {// 将元素映射到每一个桶去int bucketIndex = (int) (num * k);buckets.get(bucketIndex).add(num);}// 对桶里面的每个元素排序for (List<Float> bucket : buckets) {Collections.sort(bucket);}// 合并每个排序好的桶元素int index = 0;for (List<Float> bucket : buckets) {for (Float aFloat : bucket) {nums[index++] = aFloat;}}}
9、基数排序(Radix Sort)
基数排序(Radix Sort):根据键值的每位数字来分配桶,从最低有效位开始排序,然后收集;再从次低位开始排序…以此类推,直到最高有效位。
其他相关内容
1. 哈希-矩阵解题心得(一):https://blog.csdn.net/a147775/article/details/143558612
2. 链表-堆解题心得(二):https://blog.csdn.net/a147775/article/details/144218993
相关文章:

力扣hot100道【贪心算法后续解题方法心得】(三)
力扣hot100道【贪心算法后续解题方法心得】 十四、贪心算法关键解题思路1、买卖股票的最佳时机2、跳跃游戏3、跳跃游戏 | |4、划分字母区间 十五、动态规划什么是动态规划?关键解题思路和步骤1、打家劫舍2、01背包问题3、完全平方式4、零钱兑换5、单词拆分6、最长递…...

工业齐套管理虚拟现实仿真模拟软件
工业齐套管理虚拟现实仿真模拟软件是与法国最大的汽车制造商合作开发的一款虚拟现实仿真模拟软件,借助身临其境的虚拟现实环境,无需停止生产线,即可模拟仓库和提货区域。 工业齐套管理虚拟现实仿真模拟软件不仅适用于汽车工业,安全…...

ARP表、MAC表、路由表的区别和各自作用
文章目录 ARP表、MAC表、路由表的区别和各自作用同一网络内:ARP表request - 请求reply - 响应 MAC地址在同一网络内,交换机如何工作? 不同网络路由表不同网络通信流程PC1到路由器路由器到PC2流程图 简短总结 ARP表、MAC表、路由表的区别和各自作用 拓扑图如下: 同一网络内:…...

Android 使用OpenGLES + MediaPlayer 获取视频截图
概述 Android 获取视频缩略图的方法通常有: ContentResolver: 使用系统数据库MediaMetadataRetriever: 这个是android提供的类,用来获取本地和网络media相关文件的信息ThumbnailUtils: 是在android2.2(api8)之后新增的一个,该类为…...

浏览器的事件循环机制
浏览器和Node的事件循环机制 引言浏览器的事件循环机制 引言 由于JS是单线程的脚本语言,所以在同一时间只能做一件事情,当遇到多个任务时,我们不可能一直等待任务完成,这会造成巨大的资源浪费。为了协调时间,用户交互…...

Z2400032基于Java+Mysql+SSM的校园在线点餐系统的设计与实现 代码 论文
在线点餐系统 1.项目描述2. 技术栈3. 项目结构后端前端 4. 功能模块5. 项目实现步骤注意事项 6.界面展示7.源码获取 1.项目描述 本项目旨在开发一个校园在线点餐系统,通过前后端分离的方式,为在校学生提供便捷的餐厅点餐服务,同时方便餐厅和…...

k8s使用的nfs作为sc。
k8s使用的nfs作为sc。 当前出现一个问题: 1.有一个pod他是通过流进行文件解压并写入到nfs服务器对应的目录中。 2.一个大压缩包下有20多个压缩包,递归解压。解压完成后应该是20多个文件夹,文件夹下有.json文件。 3.pod中的程序解压后去找以.j…...

linux下Qt程序部署教程
文章目录 [toc]1、概述2、静态编译安装Qt1.1 安装依赖1.2 静态编译1.3 报错1.4 添加环境变量1.5 下载安装QtCreator 3、配置linuxdeployqt环境1.1 在线安装依赖1.2 使用linuxdeployqt提供的程序1.3 编译安装linuxdeployqt 4、使用linuxdeployqt打包依赖1.1 linuxdeployqt使用选…...
)
tp6 合成两个pdf文件(附加pdf或者替换pdf)
最近在做项目有个需求,项目中需要根据设置的html合同模板自动生成PDF合同供客户下载签署,并根据回传的已签署合同尾页来替换原来未签署合同的尾页,合成新的已签署合同文本。 读取两个PDF文件并合成的 具体代码记录如下: use set…...
工作:三菱PLC防止程序存储器爆满方法
工作:三菱PLC防止程序存储器爆满方法 一、防止程序存储器爆满方法1、编程时,添加行注释时,记得要选“外围”,这样不会占用PLC程序存储器内存;2、选择“外围”的注释,前面会有个*星号,方便检查 二…...

jmeter 获取唯一全局变量及多线程读写的问题
一、jmeter 获取唯一ID号全局变量 在JMeter中获取唯一ID号并设置为全局变量,可以通过以下几种方法实现: 使用JMeter内置的UUID函数: JMeter提供了一个内置的函数__UUID,可以生成一个随机的UUID,这个UUID是全局唯一的。…...
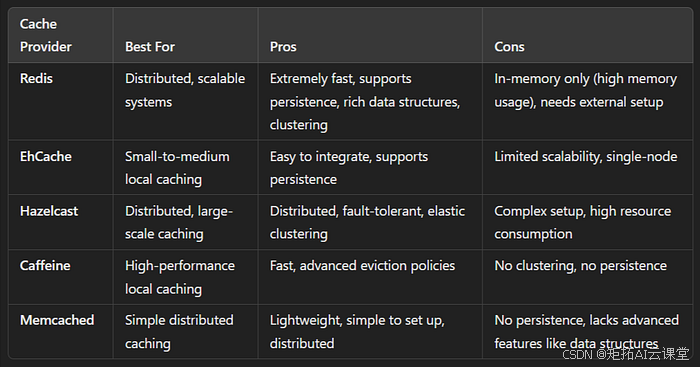
掌握 Spring Boot 中的缓存:技术和最佳实践
缓存是一种用于将经常访问的数据临时存储在更快的存储层(通常在内存中)中的技术,以便可以更快地满足未来对该数据的请求,从而提高应用程序的性能和效率。在 Spring Boot 中,缓存是一种简单而强大的方法,可以…...
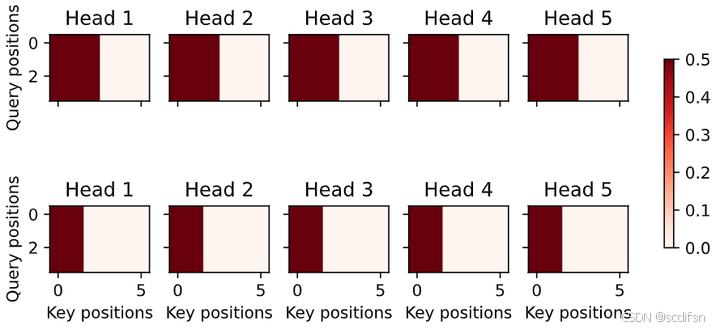
动手学深度学习10.5. 多头注意力-笔记练习(PyTorch)
本节课程地址:多头注意力代码_哔哩哔哩_bilibili 本节教材地址:10.5. 多头注意力 — 动手学深度学习 2.0.0 documentation 本节开源代码:...>d2l-zh>pytorch>chapter_multilayer-perceptrons>multihead-attention.ipynb 多头注…...
)
13 设计模式之外观模式(家庭影院案例)
一、什么是外观模式? 1.定义 在日常生活中,许多人喜欢通过遥控器来控制家中的电视、音响、DVD 播放器等设备。虽然这些设备各自独立工作,但遥控器提供了一个简洁的界面,让用户可以轻松地操作多个设备。而这一设计理念正是 外观模…...

单片机学习笔记 12. 定时/计数器_定时
更多单片机学习笔记:单片机学习笔记 1. 点亮一个LED灯单片机学习笔记 2. LED灯闪烁单片机学习笔记 3. LED灯流水灯单片机学习笔记 4. 蜂鸣器滴~滴~滴~单片机学习笔记 5. 数码管静态显示单片机学习笔记 6. 数码管动态显示单片机学习笔记 7. 独立键盘单片机学习笔记 8…...

Web安全基础实践
实践目标 (1)理解常用网络攻击技术的基本原理。(2)Webgoat实践下相关实验。 WebGoat WebGoat是由著名的OWASP负责维护的一个漏洞百出的J2EE Web应用程序,这些漏洞并非程序中的bug,而是故意设计用来讲授We…...

Zookeeper集群数据是如何同步的?
大家好,我是锋哥。今天分享关于【Zookeeper集群数据是如何同步的?】面试题。希望对大家有帮助; Zookeeper集群数据是如何同步的? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 Zookeeper集群中的数据同步是通过一种称为ZAB(Zo…...
SpringCloud框架学习(第六部分:Sentinel实现熔断与限流)
目录 十四、SpringCloud Alibaba Sentinel实现熔断与限流 1.简介 2.作用 3.下载安装 4.微服务 8401 整合 Sentinel 入门案例 5.流控规则 (1)基本介绍 (2)流控模式 Ⅰ. 直接 Ⅱ. 关联 Ⅲ. 链路 (3࿰…...
动态规划-----路径问题
动态规划-----路径问题 下降最小路径和1:状态表示2:状态转移方程3 初始化4 填表顺序5 返回值6 代码实现 总结: 下降最小路径和 1:状态表示 假设:用dp[i][j]表示:到达[i,j]的最小路径 2:状态转…...

Rust循环引用与多线程并发
循环引用与自引用 循环引用的概念 循环引用指的是两个或多个对象之间相互持有对方的引用。在 Rust 中,由于所有权和生命周期的严格约束,直接创建循环引用通常会导致编译失败。例如: // 错误的循环引用示例 struct Node {next: Option<B…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
