递归求最大公约数
#include <stdio.h>// 函数声明
int gcd(int a, int b);int main() {int x, y;printf("请输入两个正整数:");scanf("%d %d", &x, &y);printf("最大公约数是:%d\n", gcd(x, y));return 0;
}// 递归求最大公约数
int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);
}这种方法可以求最大公约数,因为它基于欧几里得算法(Euclidean algorithm),这是一种古老而高效的算法,用于计算两个整数的最大公约数(GCD)。欧几里得算法的核心思想是:两个整数的最大公约数与较小数和两数相除余数的最大公约数相同。
这里是欧几里得算法的基本原理:
1. 基本情况:如果其中一个数变为0,那么另一个数就是最大公约数。因为任何数和0的最大公约数都是它本身。
2. 递归步骤:对于任意两个正整数`a`和`b`(假设`a > b`),它们的最大公约数与`b`和`a % b`(`a`除以`b`的余数)的最大公约数相同。这是因为`a`可以表示为`a = bq + r`,其中`q`是商,`r`是余数。那么`a`和`b`的公约数也必定是`b`和`r`的公约数。
3. 重复应用:通过不断重复这个过程,直到其中一个数变为0,另一个数就是最大公约数。
这个算法之所以有效,是因为它利用了除法的性质和最大公约数的定义。每次递归调用实际上是在缩小问题的规模,直到达到基本情况。:
以一个具体的例子来说明:
假设我们要计算48和18的最大公约数
1. `48`和`18`的最大公约数与`18`和`48 % 18`(即`48`除以`18`的余数,也就是`12`)的最大公约数相同。
2. 然后我们计算`GCD(18, 12)`,这与`12`和`18 % 12`(即`6`)的最大公约数相同。
3. 接着计算`GCD(12, 6)`,这与`6`和`12 % 6`(即`0`)的最大公约数相同。
4. 由于其中一个数现在是`0`,算法终止,另一个数`6`就是`48`和`18`的最大公约数。
相关文章:

递归求最大公约数
#include <stdio.h>// 函数声明 int gcd(int a, int b);int main() {int x, y;printf("请输入两个正整数:");scanf("%d %d", &x, &y);printf("最大公约数是:%d\n", gcd(x, y));return 0; }// 递归求最大公约…...

关于在浏览器里面获取手机方向的事件
先说问题:浏览器有一个自带原生的获取手机方向的事件方法 deviceorientation: https://developer.mozilla.org/en-US/docs/Web/API/DeviceOrientationEvent/DeviceOrientationEvent 这个事件里面有个实例absolute 看名字知道意思吧,对就是绝对坐标的意…...

STM32 出租车计价器系统设计(一) 江科大源码改写
STM32 出租车计价器系统设计 功能目标 驱动步进电机模拟车轮旋转,并实现调速功能。 设置车轮周长和单价,检测车轮转速和运转时间。 计算并显示行驶里程和价格。 硬件材料 28BYJ48 五线四相步进电机和 ULN2003 驱动板模块 测速传感器模块 嵌入式小系统…...
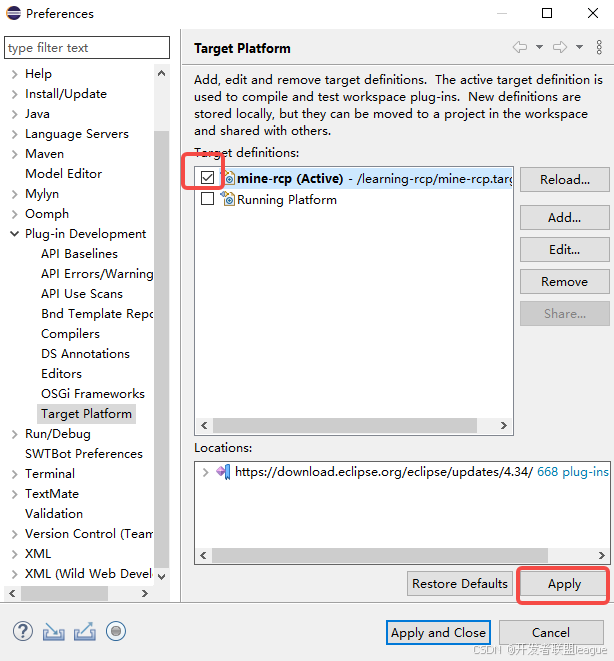
eclipse rcp-创建rcp-创建target
1.创建一个target文件,将其命名为mine-rcp.target 2. 编辑target 2.1 点击add按钮,选中software site 2.2 选择一个software site 打开浏览器。 选择一个合适的eclipse作为基础版本。进入https://download.eclipse.org/eclipse/downloads/https://dow…...

微信小程序--创建一个日历组件
微信小程序–创建一个日历组件 可以创建一个日历组件,来展示当前月份的日期,并支持切换月份的功能。 一、目录结构 /pages/calendarcalendar.wxmlcalendar.scsscalendar.jscalendar.json二、calendar.wxml <view class"calendar"><…...

质量问题分析与改进常见方法
大同小异,本质都是定位、解决、推广三大步双归零 技术归零五条要求:“定位准确、机理清楚、问题复现、措施有效、举一反三”。 管理归零五条要求:“过程清楚、责任明确、措施落实、严肃处理、完善规章”。 航天FRACASFRACAS ,是“…...

质数的和与积
质数的和与积 C语言代码C 代码Java代码Python代码 💐The Begin💐点点关注,收藏不迷路💐 两个质数的和是S,它们的积最大是多少? 输入 一个不大于10000的正整数S,为两个质数的和。 输出 一个整…...

数据结构 (35)分配类排序
前言 分配类排序是数据结构中的一种重要排序方法,其核心思想是利用分配和收集过程对元素进行排序,而无需比较元素之间的关键字。这种方法突破了基于关键字比较的排序算法的时间下界,可以达到线性时间复杂度O(n)。 一、分配类排序的基本概念 分…...

Cesium隐藏默认控件
终于有时间开始整理下知识点了。 开搞 本地环境 vue3vitecesiumvite和cesium都是最新版本这里有个问题需要注意,就是如何为Cesium配置Vite,随便检索一下,大部分都时通过插件【vite-plugin-cesium】作为解决方案,我本地创建新的示…...
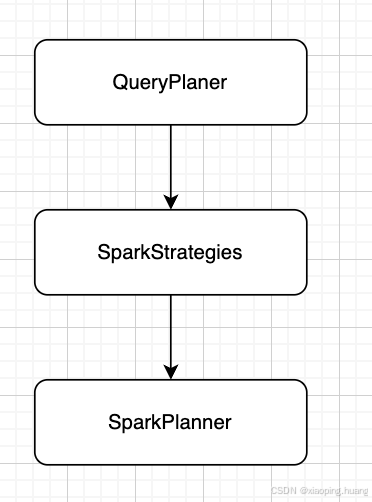
Spark SQL 执行计划解析源码分析
本文用于记录Spark SQL执行计划解析的源码分析。文中仅对关键要点进行提及,无法面面具到,仅描述大体的框架。 Spark的Client有很多种,spark-sql,pyspark,spark- submit,R等各种提交方式,这里以…...

rabbitMq举例
新来个技术总监,把 RabbitMQ 讲的那叫一个透彻,佩服! 生产者 代码举例 public String sendMsg(final String exchangeName,final String routingKey,final String msg) {} /*** 发送消息* param exchangeName exchangeName* param routin…...

奇怪的知识又增加了:ESP32下的Lisp编程=>ULisp--Lisp for microcontrollers
ESP32下有MicroPython,那么我就在想,有Lisp语言支持吗?答案是果然有!有ULisp,专门为MCU设计的Lisp! 网址:uLisp - Lisp for microcontrollers 介绍:用于微控制器的 Lisp 适用于 Ar…...

渗透测试之信息收集
免责声明:使用本教程或工具,用户必须遵守所有适用的法律和法规,并且用户应自行承担所有风险和责任。 文章目录 1. 基础信息收集2. 网络资产发现3. 网站和应用信息4. 技术栈识别5. 安全漏洞和配置6. 移动应用分析7.Google语法常见Google使用场…...

基本分页存储管理
一、实验目的 目的:熟悉并掌握基本分页存储管理的思想及其实现方法,熟悉并掌握基本分页存储管理的分配和回收方式。 任务:模拟实现基本分页存储管理方式下内存空间的分配和回收。 二、实验内容 1、实验内容 内存空间的初始化——可以由用户输…...
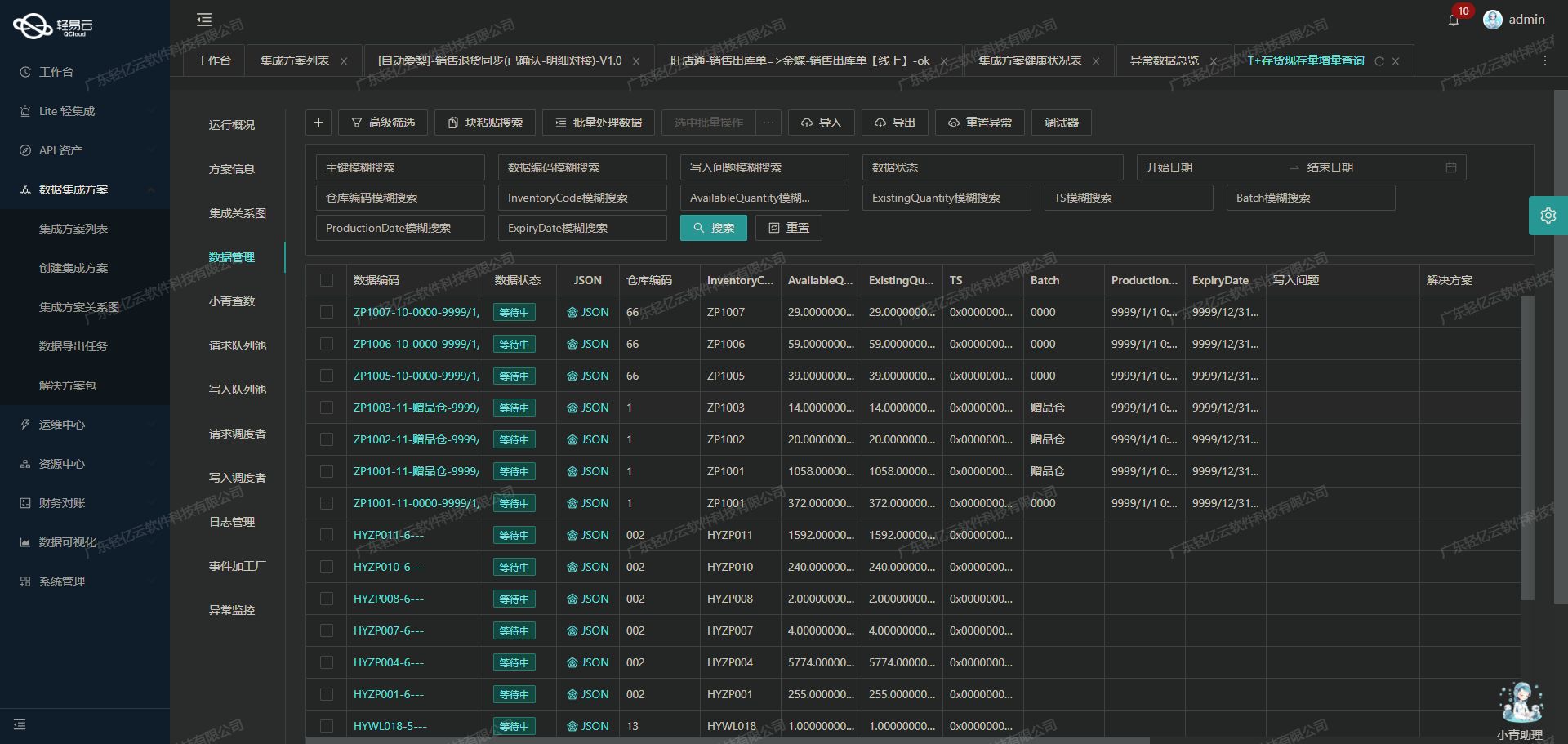
SQLServer到MySQL的数据高效迁移方案分享
SQL Server数据集成到MySQL的技术案例分享 在企业级数据管理中,跨平台的数据集成是一个常见且关键的任务。本次我们将探讨如何通过轻易云数据集成平台,将巨益OMS系统中的退款单明细表从SQL Server高效、安全地迁移到MySQL数据库中。具体方案名称为“7--…...

软考:工作后再考的性价比分析
引言 在当今的就业市场中,软考(软件设计师、系统分析师等资格考试)是否值得在校学生花费时间和精力去准备?本文将从多个角度深入分析软考在不同阶段的性价比,帮助大家做出明智的选择。 一、软考的价值与局限性 1.1 …...

shell编程(完结)
shell编程(完结) 声明! 学习视频来自B站up主 泷羽sec 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章 笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其…...

UNIX数据恢复—UNIX系统常见故障问题和数据恢复方案
UNIX系统常见故障表现: 1、存储结构出错; 2、数据删除; 3、文件系统格式化; 4、其他原因数据丢失。 UNIX系统常见故障解决方案: 1、检测UNIX系统故障涉及的设备是否存在硬件故障,如果存在硬件故障…...

adb连接逍遥安卓模拟器失败的问题解决方案
1、逍遥安卓模拟器进入系统应用,设置-关于平板电脑-版本号,连续点击3次以上,直到提示进入开发者模式,返回设置界面,进入【开发者选项】-【USB调试】开启,之后重启模拟器再次adb尝试连接。 2、android stud…...

【昇腾】NPU ID:物理ID、逻辑ID、芯片映射关系
起因: https://www.hiascend.com/document/detail/zh/Atlas%20200I%20A2/23.0.0/re/npu/npusmi_013.html npu-smi info -l查询所有NPU设备: [naienotebook-npu-bd130045-55bbffd786-lr6t8 DCNN]$ npu-smi info -lTotal Count : 1NPU…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
