自定义函数库
求两点距离
double dis(double x1, double y1, double x2, double y2){return sqrt(pow(x2-x1, 2)+pow(y2-y1, 2));
}
判断闰年
bool isLeapYear(int year){return year%4==0 && year%100!=0 || year%400==0;
}
判断素数
bool isPrime(int num){if(num<2) return false;for(int i=2; i*i<=num; i++){if(num%i == 0) return false; }return true;
}
埃氏筛素数
const int N=1e5+1;
bool is_prime[N];
void func(){memset(is_prime, true, sizeof(is_prime));is_prime[0]=is_prime[1]=false;for(int i=2; i*i<=N; i++){if(is_prime[i]){for(int j=i*i; j<=N; j=j+i){is_prime[j]=false;}}}
}
冒泡排序
const int N=101;
int n, arr[N];
void bubbleSort() {for(int i=0; i<n-1; i++) {//比较趟数 bool flag = 1;for(int j=0; j<n-i-1; j++) { if(arr[j] > arr[j+1]) {swap(arr[j], arr[j+1]);flag = 0;}}if(flag) break;}
}
插入排序
const int N=101;
int n, arr[N];
void insertSort() {for(int i=1; i<n; i++) {//arr[i]当前需要插入的元素int base=arr[i], j; for(j=i-1; j>=0; j--) {if(arr[j]>base) {arr[j+1]=arr[j];}else break;}arr[j+1]=base;}
}
选择排序
const int N=101;
int n, arr[N];
void selectSort() {for(int i=0; i<n-1; i++) {//i:当次排序元素应该在的位置 int minIndex=i;for(int j=i+1; j<n; j++) {if(arr[j] < arr[minIndex]) {minIndex = j;}}swap(arr[minIndex], arr[i]);}
}
归并排序
const int N=101;
int n, arr[N], tmp[N];
void mergeSort(int left, int right){int mid=(left+right)/2;if(left<mid) partition(left, mid);if(mid+1<right) partition(mid+1, right);int i=left, j=mid+1, t=0;while(i<=mid && j<=right){if(arr[i] < arr[j]) tmp[t++] = arr[i++];else tmp[t++] = arr[j++];}while(i<=mid) tmp[t++] = arr[i++];while(j<=right) tmp[t++] = arr[j++];for(int i=0; i<t; i++) arr[i+left] = tmp[i];
}
快速排序
const int N=101;
int n, arr[N];
void quickSort(int left, int right){int num = arr[left], i=left, j=right;while(i<j){while(i<j && arr[j]>=num) j--;arr[i]=arr[j];while(i<j && arr[i]<=num)i++;arr[j]=arr[i];}arr[i]=num;if(left<i-1) quickSort(left, i-1);if(i+1<right) quickSort(i+1, right);
}
排列-n个数中抽m个进行全排列
const int N=10;
int n, m, arr[N], box[N];
bool vis[N];
void dfs(int pos){if(pos==m){for(int i=0; i<m; i++) cout<<box[i]<<" ";cout<<endl;return;}for(int i=0; i<n; i++){if(!vis[i]){vis[i]=true;box[pos]=arr[i];dfs(pos+1);vis[i]=false;}}
}
组合-n个数中抽m个进行组合
const int N=10;
int n, m, arr[N], box[N];
bool vis[N];
void dfs(int idx, int pos){if(pos==m){for(int i=0; i<m; i++) cout<<box[i]<<" ";cout<<endl;return;}for(int i=idx; i<n; i++){if(!vis[i]){vis[i]=true;box[pos]=arr[i];dfs(i+1, pos+1);vis[i]=false;}}
}
高精度数加法
string add(string a, string b) {int lena=a.length(), lenb=b.length(), a1[1005]= {}, b1[1005]= {};for(int i=0; i<lena; i++) a1[lena-1-i] = a[i]-'0';for(int i=0; i<lenb; i++) b1[lenb-1-i] = b[i]-'0';int lenc=lena>lenb?lena:lenb, c1[1005]= {}, carry=0;for(int i=0; i<lenc; i++) {c1[i]=a1[i]+b1[i]+carry;carry=c1[i]/10;c1[i]%=10;}if(carry>0) c1[lenc++]=carry;string res="";for(int i=lenc-1; i>=0; i--) res += c1[i]+'0';return res;
}
高精度数减法
string sub(string a, string b) {bool f=true; //标记a和b的大小关系,默认a大 int lena=a.length(), lenb=b.length();if(lena<lenb || lena==lenb && a<b){f=false;swap(a, b);swap(lena, lenb);} int a1[1005]= {}, b1[1005]= {};for(int i=0; i<lena; i++) a1[lena-1-i] = a[i]-'0';for(int i=0; i<lenb; i++) b1[lenb-1-i] = b[i]-'0';int c1[1005]= {}, lenc=lena;for(int i=0; i<lenc; i++) {if(a1[i]<b1[i]){a1[i+1]--;a1[i]+=10;} c1[i]=a1[i]-b1[i];}while(lenc>1 && c1[lenc-1]==0) lenc--; string res="";if(f==false) res+='-';for(int i=lenc-1; i>=0; i--) res += c1[i]+'0';return res;
}
高精度数乘法,大数乘大数
string mul1(string a, string b) {int lena=a.length(), lenb=b.length(), a1[1005]= {}, b1[1005]= {};for(int i=0; i<lena; i++) a1[lena-1-i] = a[i]-'0';for(int i=0; i<lenb; i++) b1[lenb-1-i] = b[i]-'0';int lenc=lena+lenb, c1[2005]= {}, carry;for(int i=0; i<lenb; i++) {carry=0;for(int j=0; j<lena; j++) {c1[i+j]+=a1[j]*b1[i]+carry;carry = c1[i+j]/10;c1[i+j]%=10;}c1[i+lena]=carry;}while(lenc>1 && c1[lenc-1]==0) lenc--;//保存运算结果string res="";for(int i=lenc-1; i>=0; i--) res += c1[i]+'0';return res;
}
高精度数乘法,大数乘小数
string mul2(string a, int b){int lena=a.length(), a1[1005]={};for(int i=0; i<lena; i++) a1[lena-1-i]=a[i]-'0';int lenc=lena, c1[2005]={}, carry=0;for(int i=0; i<lenc; i++){c1[i] = a1[i]*b+carry;carry = c1[i]/10;c1[i] %= 10;}while(carry){c1[lenc++]=carry%10;carry/=10;}string res="";for(int i=lenc-1; i>=0; i--) res+=c1[i]+'0';return res;
}
相关文章:

自定义函数库
求两点距离 double dis(double x1, double y1, double x2, double y2){return sqrt(pow(x2-x1, 2)pow(y2-y1, 2)); }判断闰年 bool isLeapYear(int year){return year%40 && year%100!0 || year%4000; }判断素数 bool isPrime(int num){if(num<2) return false;f…...

FreeRTOS例程2-任务挂起恢复与使用中断遇到的坑!
任务挂起简单点理解就是现在不需要执行这个任务,让它先暂停,就是挂起。恢复就是从刚才挂起的状态下继续运行。 API函数 任务挂起vTaskSuspend() 函数原型(tasks.c中): void vTaskSuspend( TaskHandle_t xTaskToSuspend ) 1. 参数: xTaskTo…...

L23.【LeetCode笔记】验证回文串(剖析几种解法)
目录 1.题目 2.自解 提交结果 反思 大小写之间的位运算 提交结果 3.代码优化 提交结果 编辑 4.LeetCode网友提供的解法 1.题目 https://leetcode.cn/problems/XltzEq/description/ 给定一个字符串 s ,验证 s 是否是 回文串 ,只考虑字母和数…...

FPGA 17 ,FPGA 与 SR-IOV虚拟化技术,高性能计算与虚拟化技术的结合(FPGA 与 SR-IOV 和 PCI,高性能计算与虚拟化的完美融合)
目录 前言 一. SR-IOV 的起源与发展 1. SR-IOV 的起源与时间线 2. SR-IOV 的诞生原因 3. SR-IOV 的详细介绍 二. SR-IOV 和 PCI 之间的关系 三. PCI 的起源与演进 1. PCI 的起源与时间线 2. PCI 的关键特性 四. FPGA 的独特魅力 1. FPGA 的定义与特性 2. FPGA 的内…...

解决navicat 导出excel数字为科学计数法问题
一、原因分析 用程序导出的csv文件,当字段中有比较长的数字字段存在时,在用excel软件查看csv文件时就会变成科学技术法的表现形式。 其实这个问题跟用什么语言导出csv文件没有关系。Excel显示数字时,如果数字大于12位,它会自动转化…...

[Unity] AppLovin Max接入Native 广告 Android篇
把下载下来的maxnativelibrary-release-文件放在Plugins/Android下 将这一行加入到mainTemplate.gradle文件中 implementation androidx.constraintlayout:constraintlayout:2.1.4添加下面的两个脚本 using System; using System.Collections; using System.Collections.Gener…...

Source Insight 4.0的安装
一、安装与破解 1、下载Source Insight 4.0安装包 https://pan.baidu.com/s/1t0u1RM19am0lyzhlNTqK9Q?pwdnvmk 2、下载程序破解补丁包 https://pan.baidu.com/s/1irvH-Kfwjf4zCCtWJByqJQ 其中包含文件si4.pediy.lic 和 sourceinsight4.exe。 3、安装下载的Source Insight …...

远程调试软件对比与使用推荐
远程调试软件对比与使用推荐 远程调试是现代软件开发中不可或缺的一部分,尤其是在处理分布式系统、云端服务或远程服务器上的问题时。以下是对几种常见远程调试工具的详细对比和推荐使用场景。 1. GDB (GNU Debugger) 特点 开源:完全免费且开源&…...
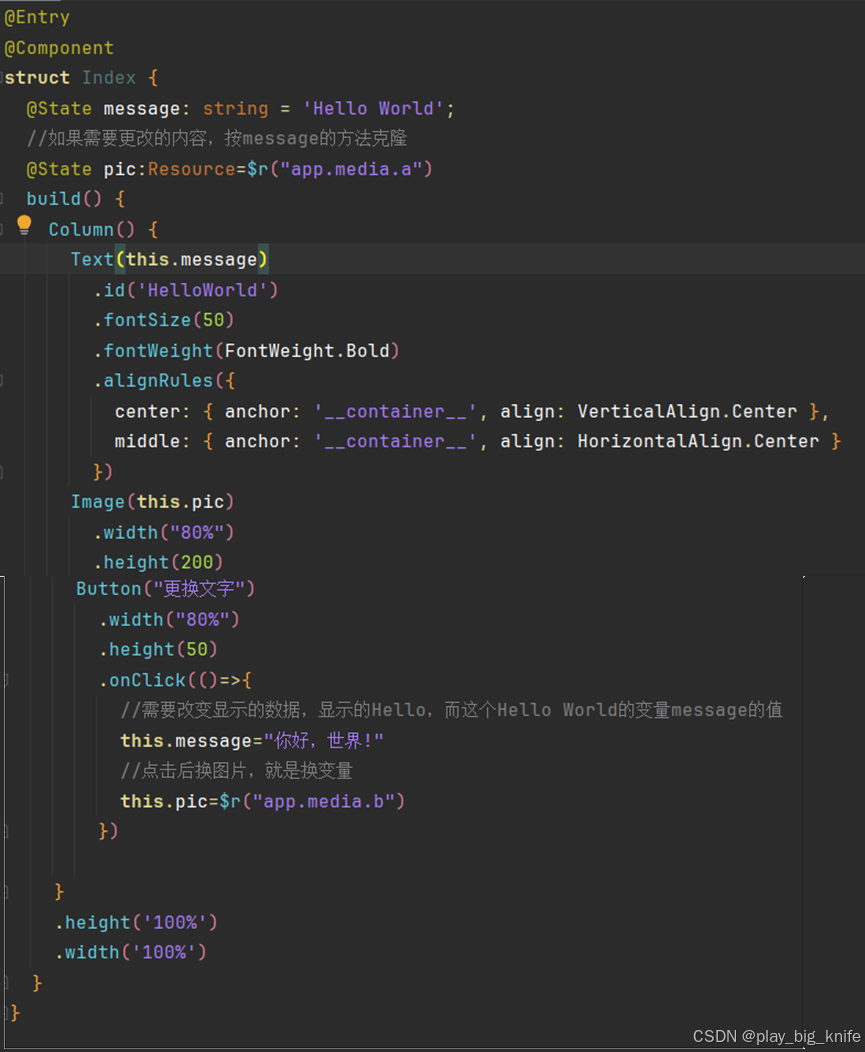
鸿蒙项目云捐助第二讲鸿蒙图文互动基本程序实现
鸿蒙项目云捐助第二讲鸿蒙图文互动基本程序实现 结合第一讲建立的“Hello World”程序,得到如下图所示的界面。 这里的“Hello World”是通过“Priview”显示出来的。在这个界面中进行开发的前奏曲,可以通过点击更换图片的案例来体会一下鸿蒙Next的开发…...

求解球面的一组正交标架
目录 求解球面的一组正交标架 求解球面的一组正交标架 球面 r ( u , v ) ( a cos u cos v , a cos u sin v , a sin u ) \mathbf{r}(u,v)\left(a\cos u\cos v,a\cos u\sin v,a\sin u\right) r(u,v)(acosucosv,acosusinv,asinu), 求得 r u ( − a sin u c…...

php.ini 文件上传/执行时间/部分配置新手教程
1、上传文件大小配置 一般需要同时配置“upload_max_filesize”、“post_max_size”,配置格式如下: file_uploads On ;是否允许HTTP文件上传 upload_max_filesize 2M ;设置单个文件上传的最大尺寸 post_max_size 8M ;设置 POST 请求体的最大尺寸&am…...

【Leetcode Top 100】102. 二叉树的层序遍历
问题背景 给你二叉树的根节点 r o o t root root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 数据约束 树中节点数目在范围 [ 0 , 2000 ] [0, 2000] [0,2000] 内 − 1000 ≤ N o d e . v a l ≤ 1000 -1…...

【C++笔记】AVL树
前言 各位读者朋友们大家好,上期我们讲解了map和set这两大容器的使用,这一期我们讲解最早的平衡二叉搜索树——AVL树。 目录 前言一. AVL树的概念二. AVL树的实现2.1 AVL树的结构2.2 AVL树的插入2.2.1 AVL树插入一个值的大致过程2.2.2 平衡因子的更新2…...

【竞技宝】LOL:JDG官宣yagao离队
北京时间2024年12月13日,在英雄联盟S14全球总决赛结束之后,各大赛区都已经进入了休赛期,目前休赛期也快进入尾声,LPL大部分队伍都开始陆续官宣转会期的动向,其中JDG就在近期正式官宣中单选手yagao离队,而后者大概率将直接选择退役。 近日,JDG战队在官方微博上连续发布阵容变动消…...

双目摄像头标定方法
打开matlab 找到这个标定 将双目左右目拍的图像上传(左右目最好不少于20张) 等待即可 此时已经完成标定,左下角为反投影误差,右边为外参可视化 把这些误差大的删除即可。 点击导出 此时回到主页面,即可看到成功导出 Ca…...

相差不超过k的最多数,最长公共子序列(一),排序子序列,体操队形,青蛙过河
相差不超过k的最多数 链接:相差不超过k的最多数 来源:牛客网 题目描述: 给定一个数组,选择一些数,要求选择的数中任意两数差的绝对值不超过 𝑘 。问最多能选择多少个数? 输入描述: 第一行输入两个正整…...
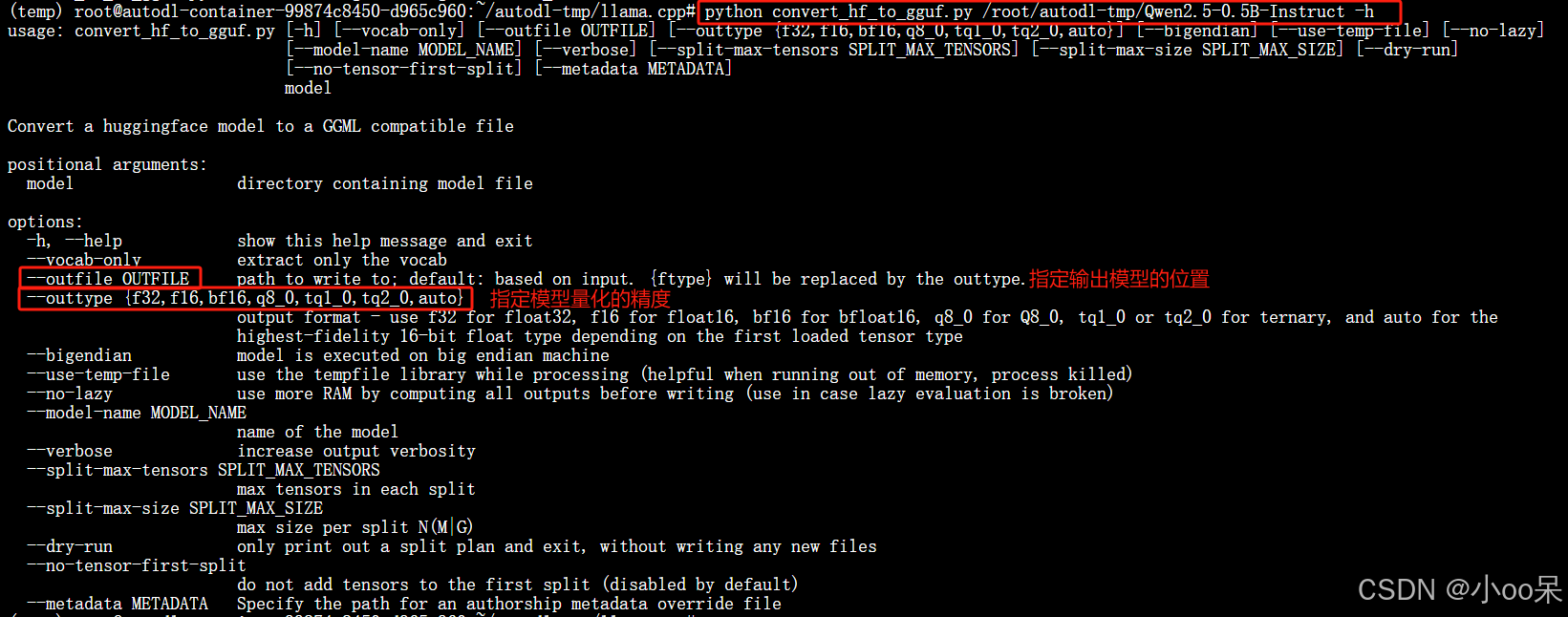
【自然语言处理与大模型】使用llama.cpp将HF格式大模型转换为GGUF格式
llama.cpp的主要目标是在本地和云端的各种硬件上以最小的设置和最先进的性能实现LLM推理。是一个专为大型语言模型(LLM)设计的高性能推理框架,完全使用C和C编写,没有外部依赖,这使得它可以很容易地被移植到不同的操作系…...

MongoDB存储照片和文件存储照片的区别在那里?
一、维度对比 比较维度MongoDB存储照片文件系统存储照片数据模型使用文档存储数据,可以存储不同结构的照片。以文件的形式存储照片,每个文件独立存在。性能高效的数据检索,适用于大规模应用程序中的高效检索和访问。但在处理大量高分辨率图片…...

协变量的概念
协变量的概念 协变量的概念 协变量(Covariate)是在统计分析和研究中,与因变量(被研究的主要变量)相关,并且可能对因变量产生影响的其他变量。它不是研究的主要关注对象,但需要在分析过程中被考虑进去,因为它可能会混淆或改变自变量与因变量之间的关系。举例说明 教育研…...

【[LeetCode每日一题】Leetcode 1768.交替合并字符串
Leetcode 1768.交替合并字符串 题目描述: 给定两个字符串 word1 和 word2,以交替的方式将它们合并成一个新的字符串。即,第一个字符来自 word1,第二个字符来自 word2,第三个字符来自 word1,依此类推。如果…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
