【算法day17-day18】回溯:解决组合问题
不好意思呀各位,最近在忙期末考今天才彻底结束,来让我们继续算法之路吧~
题目引用
- 组合
- 电话号码的字母组合
- 组合总和
- 组合总和II
- 分割回文串
1.组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
我们来看这道回溯入门题,首先呢我要说一下我对回溯的想法,在我看来回溯其实就是在不断递归的过程中形成了一颗多叉树,那么它是个树,我们就可以对其的路径进行记录,剪枝,判断等等一系列操作,从而形成一系列的结果集合。
拿这道题目举例,我们创建一个全局的res用于记录结果,path用于记录多叉树的每一条路径,创建一个递归函数,先设定函数的出口:当我们记录的path.size()==k时,就说明已经得到一种结果了,将path加入到结果数组中。那么递归函数的主体就是把1到n的数都遍历一遍,在每条路径中加入当前数值,再递归下一个元素,返回后pop掉。这其实就是记录树的路径,在前些天讲二叉树时已经讲过了。
那么来看代码:
class Solution {
public:vector<int> path;vector<vector<int>> res;void backtracking(int n,int k,int startIndex){if(path.size()==k){res.push_back(path);return;} for(int i=startIndex;i<=n;i++){path.push_back(i);backtracking(n,k,i+1);path.pop_back();}return;}vector<vector<int>> combine(int n, int k) {backtracking(n,k,1);return res;}
};
怎么样,应该比前几天题目简单不少吧。
2.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
来看这道题目,我们乍一眼一看是不是头都大了,不知道怎么才能解决这种问题。不急~只要我们慢慢分析总能分析出个一二三四,首先是电话号码对应的字母,我们肯定需要一个表来进行映射,再就是如果我们使用回溯的思想,那么就要看一下是不是和上一道题相同,不同的话应该怎么修改。
可以确定的是,这题和上一道题是不太一样的。第一、递归出口不一样。第二、每一层所能选择的元素数目和和元素本身的大小是不确定的。但是好在都能够通过遍历一遍字符串,逐层处理,逐层确定。
那么来解决这道题吧。首先,我们不能使用startIndex来确定每一层的开始位置,而是使用Index来作为源字符串内数字的定位,然后通过数字在我们自己写好的表中找到对应的数字代表的字符串,然后这样每一层的元素才确定了下来,再去回溯就很简单的解决了。
来看代码:
class Solution {
public:string digitsmap[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};vector<string> res;string path;void backtracking(string digits,int Index){if(Index==digits.size()){res.push_back(path);return;}int digit=digits[Index]-'0';string letter=digitsmap[digit];for(int i=0;i<letter.size();i++){path+=letter[i];backtracking(digits,Index+1);path.pop_back();}return;}vector<string> letterCombinations(string digits) {if(digits=="") return res;backtracking(digits,0);return res;}
};
这样写,轻轻松松100%啦
3.组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
做完上面那道题,做这道题就是小卡拉米了。需要注意的不过是从数组里面直接取出来和可重复,但是只要把握住这两个点,其实就不会很难。
来看代码:
class Solution {
public:vector<vector<int>> res;vector<int> path;void backtracking(vector<int>& candidates,int targetSum,int sum,int startIndex){if(sum>targetSum) return;if(sum==targetSum){res.push_back(path);return;}for(int i=startIndex;i<candidates.size()&&sum<targetSum;i++){sum+=candidates[i];path.push_back(candidates[i]);backtracking(candidates,targetSum,sum,i);sum-=candidates[i];path.pop_back();}return;}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates,target,0,0);return res;}
};
是不是简简单单呀~
4.组合总和II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
我们可以看一下这道题和上一道题目的区别,不可重复且只能使用一次。条件是比较苛刻的,所以我们就自己加一点工具来限制住这个多叉树的发展,其实就有一点点像剪枝了。这里我们加上一个used数组来判断这个数是否被用过,再在递归时将startIndex+1就可以了。
这里来看代码:
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true,说明同一树枝candidates[i - 1]使用过// used[i - 1] == false,说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序,让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};这里大家是不是对树枝和树层比较困惑呢,因为同一树层使用过说明我之前已经在这个位置取过这个数了,那么我现在再取肯定时重复的,同一树枝取过说明我们这一条路径上有一样的元素,但是并不是重复取的,所以是可以入到path里面的。这样说会不会好一点。
5.分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是
回文串
。返回 s 所有可能的分割方案。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
这道题目就比较难想到了。我们利用startIndex来分割题目给的字符串,分割完以后判断这个字符串是不是回文,是就赋值给path,不是就直接开始下一个循环。判断是不是回文串的方法有很多,我们这里采用我们三周之前学过的二分法来做判断(是不是不记得了)。那么这道题目就做完了。其实这些题目看到答案后都不会觉得很难,但难的是想出答案的过程,而这也是区分大家的过程。
来看代码
class Solution {
public:vector<vector<string>> res;vector<string> path;void backtracking(const string& s,int startIndex){if(startIndex>=s.size()) {res.push_back(path);return;}for(int i=startIndex;i<s.size();i++){if(ispl(s,startIndex,i)){string str=s.substr(startIndex,i-startIndex+1);path.push_back(str);}else{continue;}backtracking(s,i+1);path.pop_back();}}bool ispl(const string& s, int start, int end){for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}vector<vector<string>> partition(string s) {backtracking(s, 0);return res;}
};
总结
其实这些题目看到答案后都不会觉得很难,但难的是想出答案的过程,而这也是区分大家的过程。
相关文章:

【算法day17-day18】回溯:解决组合问题
不好意思呀各位,最近在忙期末考今天才彻底结束,来让我们继续算法之路吧~ 题目引用 组合电话号码的字母组合组合总和组合总和II分割回文串 1.组合 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回…...

从监控异常发现网络安全
前言 最近在前端异常监控系统中,发现一些异常信息,从中做了一些分析,得到一些体会,因此作文。 发现异常 某天早上打开监控系统发现,当天凌晨1点过测试环境有2个前端上报的异常,报错的原因都是由于没有获取…...
Qt之自定义标题栏拓展(十)
Qt开发 系列文章 - user-defined-titlebars(十) 目录 前言 一、方式一 1.效果演示 2.创建标题栏类 3.可视化UI设计 4.定义相关函数 5.使用标题栏类 二、方式二 1.效果演示 2.创建标题栏类 3.定义相关函数 1.初始化函数 2.功能函数 3.窗口关…...

Verilog中initial的用法
在 Verilog 语言中,initial 语句用于在仿真开始时执行一次性初始化操作。它是顺序执行的,用来描述在仿真启动时立即运行的代码块,通常用于赋初值、生成波形或控制信号行为。 语法 initial begin // 语句1 // 语句2 ... end特点 只…...

(14)D-FINE网络,爆锤yolo系列
yolo过时了?传统的yolo算法在小目标检测方面总是不行,最新算法DEIM爆锤yolo,已经替yolo解决。 一、创新点 这个算法名为DEIM,全称是DETR with Improved Matching for Fast Convergence,其主要创新点在于提出了一…...

Python :冬至快乐
第1部分:基础设置 首先创建一个新的 Python 文件,命名为 fireworks.py。 步骤 1.1: 导入必要的库 import pygame import random import sys from pygame.locals import * import math import time这些库的作用: pygame: 用于创建游戏和图…...
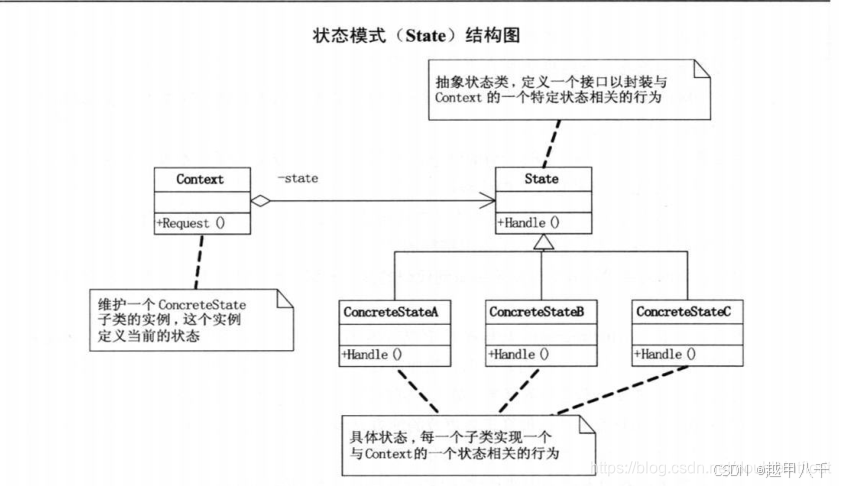
重拾设计模式--状态模式
文章目录 状态模式(State Pattern)概述状态模式UML图作用:状态模式的结构环境(Context)类:抽象状态(State)类:具体状态(Concrete State)类&#x…...
稀疏矩阵的存储与计算 gaxpy
1, gaxpy 数学公式 其中: , , 2, 具体实例 3,用稠密矩阵的方法 本节将用于验证第4节中的稀疏计算的结果 hello_gaxpy_dense.cpp #include <stdio.h> #include <stdlib.h>struct Matrix_SP {float* val; //…...
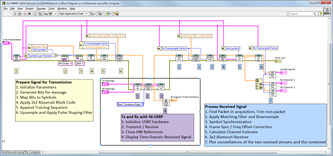
基于LabVIEW的USRP信道测量开发
随着无线通信技术的不断发展,基于软件无线电的设备(如USRP)在信道测量、无线通信测试等领域扮演着重要角色。通过LabVIEW与USRP的结合,开发者可以实现信号生成、接收及信道估计等功能。尽管LabVIEW提供了丰富的信号处理工具和图形…...
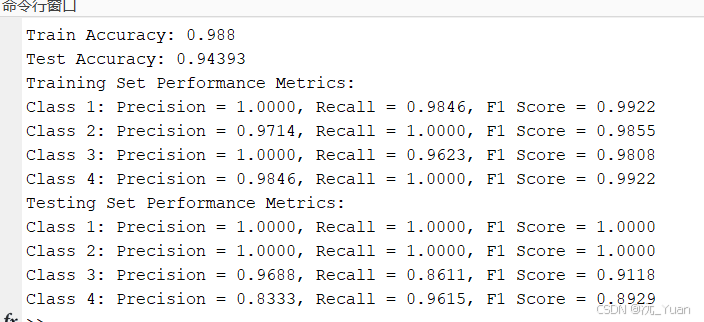
基于LSTM长短期记忆神经网络的多分类预测【MATLAB】
在深度学习中,长短期记忆网络(LSTM, Long Short-Term Memory)是一种强大的循环神经网络(RNN)变体,专门为解决序列数据中的长距离依赖问题而设计。LSTM因其强大的记忆能力,广泛应用于自然语言处理…...
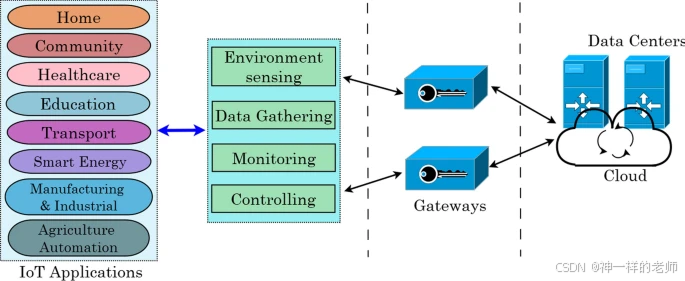
物联网:全面概述、架构、应用、仿真工具、挑战和未来方向
中文论文标题:物联网:全面概述、架构、应用、仿真工具、挑战和未来方向 英文论文标题:Internet of Things: a comprehensive overview, architectures, applications, simulation tools, challenges and future directions 作者信息&#x…...
volatility2工具的使用vol2工具篇
vol2工具 命令格式:vol.py -f [image] --profile[profile] [plugin] 1、查看系统的操作版本,系统镜像信息 2.查看用户名密码信息,当前操作系统中的password hash,例如SAM文件内容 3.从注册表提取LSA密钥信息(已解密&…...

R 基础运算
R 基础运算 R 是一种广泛使用的统计编程语言,它提供了强大的数据操作和分析功能。基础运算在 R 中非常重要,因为它们是进行更复杂计算和数据分析的基础。本文将详细介绍 R 中的基础运算,包括算术运算、逻辑运算、向量化和矩阵运算。 一、算…...
javaScriptBOM
1.1、BOM概述 1.1.1、BOM简介 BOM(browser Object)即浏览器对象模型,它提供了独立于内容而与浏览器窗口进行交互的对象,其核心对象是window。 BOM由一系列的对象构成,并且每个对象都提供了很多方法与属性 BOM缺乏标准…...

Godot RPG 游戏开发指南
Godot RPG 游戏开发指南 一、基础准备 1. 开发环境 下载并安装最新版 Godot 4.x选择使用 GDScript 或 C# 作为开发语言准备基础美术资源(角色、地图、道具等) 2. 项目结构 project/ ├── scenes/ # 场景文件 ├── scripts/ # 脚…...

目标检测数据集图片及标签同步旋转角度
前言 在深度学习领域,尤其是目标检测任务中,数据集的质量直接影响模型的性能。为了提升模型的鲁棒性和对各种场景的适应能力,数据增强技术被广泛应用于图像数据集处理。旋转角度是常见的数据增强方法,通过对图像及其对应的标签&am…...

2025前端面试热门题目——计算机网络篇
计算机网络篇——面试 1. 到底什么是 TCP 连接? TCP 连接的定义 TCP(传输控制协议)是一个面向连接的传输层协议。TCP 连接是通过 三次握手 确立的可靠数据通信链路,保证了在不可靠网络(如互联网)上的数据传输的准确…...

LEAST-TO-MOST PROMPTING ENABLES COMPLEX REASONING IN LARGE LANGUAGE MODELS---正文
题目 最少到最多的提示使大型语言模型能够进行复杂的推理 论文地址:https://arxiv.org/abs/2205.10625 摘要 思路链提示在各种自然语言推理任务中表现出色。然而,它在需要解决比提示中显示的示例更难的问题的任务上表现不佳。为了克服这种由易到难的概括…...
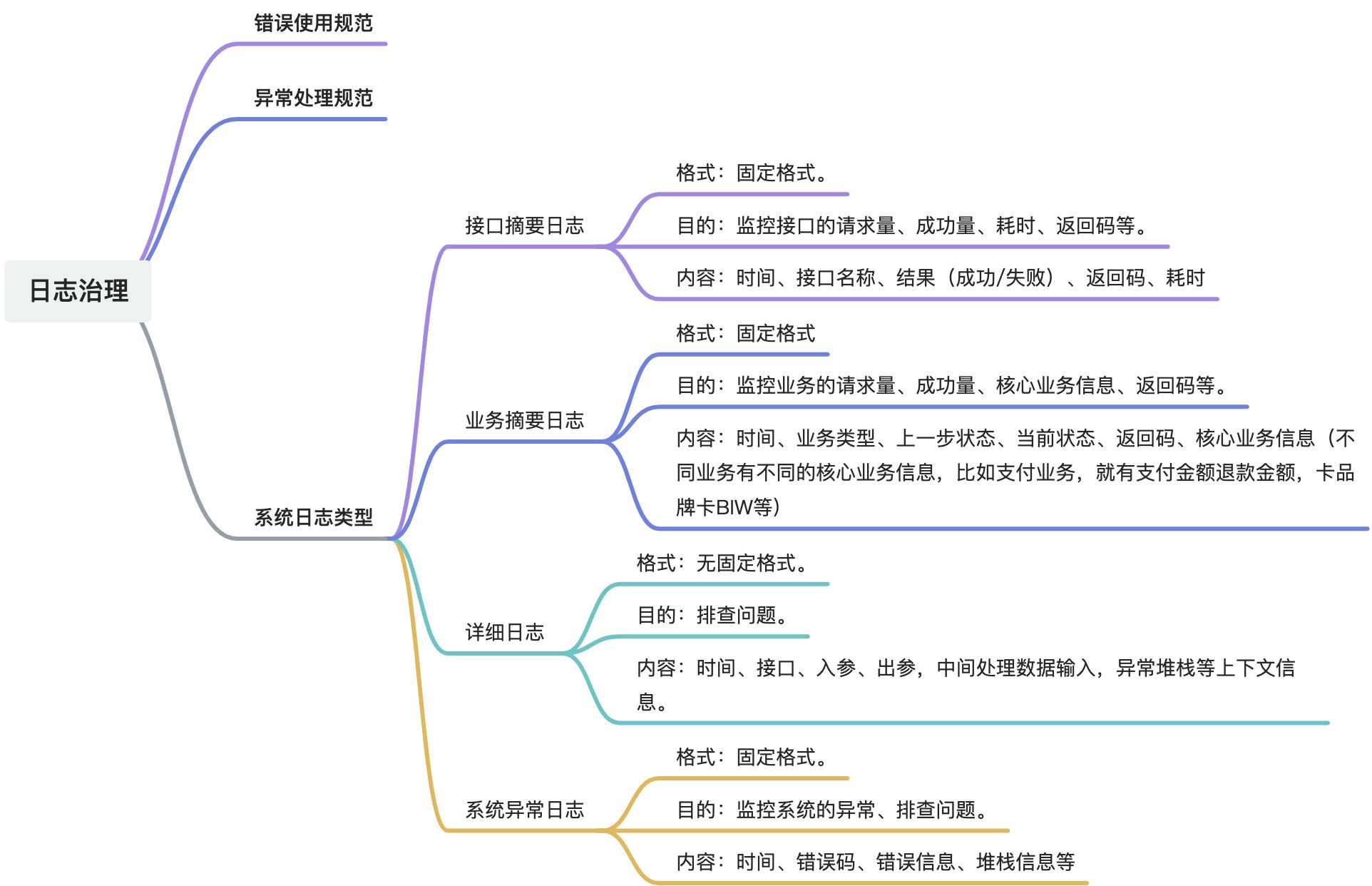
Java开发经验——日志治理经验
摘要 本文主要介绍了Java开发中的日志治理经验,包括系统异常日志、接口摘要日志、详细日志和业务摘要日志的定义和目的,以及错误码规范和异常处理规范。强调了日志治理的重要性和如何通过规范化错误码和日志格式来提高系统可观测性和问题排查效率。 1. …...
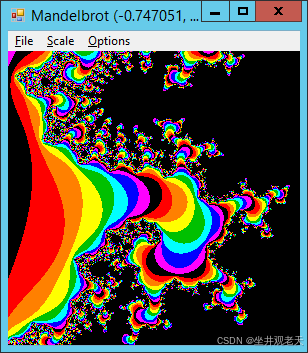
使用复数类在C#中轻松绘制曼德布洛集分形
示例在 C# 中绘制曼德布洛特集分形解释了如何通过迭代以下方程来绘制曼德布洛特集: 其中 Z(n) 和 C 是复数。程序迭代此方程,直到 Z(n) 的大小至少为 2 或程序执行最大迭代次数。 该示例在单独的变量中跟踪数字的实部和虚部。此示例使用Complex类来更轻松…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
