搜索召回:召回聚合
召回聚合
用户的查询意图往往是复杂多样的,可能涉及到不同的领域、主题和语义层面。因此,召回体系中通常通过多路召回的方式从不同角度去理解和满足用户的查询需求。此外,多路召回通过各召回通道并行计算可以在海量数据中能够快速响应,同时实现负载均衡。
在面对多个差异化设计的召回通道同时触发并返回文档的情况下,需要充分发挥各通道的优势,从大量召回候选中筛选整合以实现各通道互补,最终在保障的系统效率的同时,提高召回的准确率和业务目标的达成率,确保整体效果的最优化。召回聚合通过采用轻量级的算法策略对召回结果筛选,最终将数千篇文档传递给粗排模块进行更精细的排序操作。
蛇形合并
蛇形合并策略通过交替、蛇形的方式将来自不同通道的候选项进行融合,通常会先选择一种通道的候选项,然后交替选择其他通道的候选项。
假设有三个召回通道(A、B、C),那么可以按如下方式选取:
- 第1个候选项来自通道A
- 第2个候选项来自通道B
- 第3个候选项来自通道C
- 第4个候选项再从通道A选取,以此类推
RRF合并(Reciprocal Rank Fusion)
RRF 对来自不同召回通道的排序结果进行加权,赋予排名靠前的候选项更高的权重,最终生成一个综合排序。具体来说,对于每个检索结果,计算其在每个路径中的排名,然后取这些排名的倒数之和作为该结果的最终得分。
RRF 的计算公式如下:
R R F S c o r e ( d ) = ∑ i = 1 k 1 R a n k i ( d ) + K {\mathrm{RRF~Score}}(d)=\textstyle{\sum_{i=1}^{k}{\frac{1}{\mathrm{Rank}_{i}(d)+K}}} RRF Score(d)=∑i=1kRanki(d)+K1
其中, d d d 表示召回结果, R a n k i ( d ) \mathrm{Rank}_{i}(d) Ranki(d) 表示该结果在第 i i i 条路径中的排名, K K K 为调节参数(通常取值为60),用于平滑排名,使得即使排名较低的候选项也能获得一定的权重。
贝叶斯优化合并
贝叶斯调参可以帮助自动化调整融合策略中的参数,从而找到最优的合并方式。通过贝叶斯优化,我们可以根据召回合并过程中不同通道的重要性、权重等参数,寻找最佳的合并策略,以提升召回的质量和效率。
贝叶斯优化(Bayesian Optimization)是一种基于贝叶斯统计方法的全局优化算法,通常用于优化函数比较复杂、代价高昂、无法直接求导的情况。具体步骤如下:
-
定义目标函数:定义目标函数 f ( x ) f(x) f(x) ( x x x 是超参数)用于评估召回合并策略的效果
-
f ( w ) = M e t r i c ( M e r g e ( R e c a l l s ( w ) ) ) f(\mathbf{w})=\mathbf{Metric}(\mathbf{Merge}(\mathrm{Recalls}(\mathbf{w}))) f(w)=Metric(Merge(Recalls(w)))
-
Recalls ( w ) = [ R 1 ( w 1 ) , R 2 ( w 2 ) , … , R n ( w n ) ] \text{Recalls}(\mathbf{w}) = [R_1(w_1), R_2(w_2), \dots, R_n(w_n)] Recalls(w)=[R1(w1),R2(w2),…,Rn(wn)] 表示来自不同通道的召回结果,每个 R i ( w i ) R_i(w_i) Ri(wi) 是通道 i i i 根据权重 w i w_i wi 所返回的候选集
-
Merge ( ⋅ ) \text{Merge}(\cdot) Merge(⋅) 表示将各个通道的召回结果按权重加权融合
-
Metric ( ⋅ ) \text{Metric}(\cdot) Metric(⋅) 是根据合并后的候选集评估的性能指标
-
-
设置参数空间:如果使用加权平均的合并方式,可以将每个通道的权重作为调节参数进行优化
-
比如,设定权重参数 w = [ w 1 , w 2 , ⋅ ⋅ ⋅ , w n ] \mathbf{w}=[w_{1},w_{2},\cdot\cdot\cdot,w_{n}] w=[w1,w2,⋅⋅⋅,wn],每个召回通道的权重 w i w_{i} wi 影响候选项排名和选择
-
w = [ w 1 , w 2 , ⋅ ⋅ ⋅ , w n ] w i t h ∑ i = 1 n w i = 1 , w i ∈ [ 0 , 1 ] {\bf w}=[w_{1},w_{2},\cdot\cdot\cdot,w_{n}]\;\;\;\;\mathrm{with}\;\;\;\;\sum_{i=1}^{n}w_{i}=1,\;\;\;\;w_{i}\in[0,1] w=[w1,w2,⋅⋅⋅,wn]withi=1∑nwi=1,wi∈[0,1]
-
-
初始化高斯过程:为待优化的参数空间设定先验分布,通常使用高斯过程(Gaussian Process, GP)作为先验,表示对参数空间的初步认识
-
p ( f ( w ) ) ∼ G P ( m ( w ) , k ( w , w ′ ) ) p(f(\mathbf{w}))\sim{\mathcal{G P}}(m(\mathbf{w}),k(\mathbf{w},\mathbf{w}^{\prime})) p(f(w))∼GP(m(w),k(w,w′))
-
其中 m ( w ) m(\mathbf{w}) m(w) 是目标函数的均值函数,通常假设为零; k ( w , w ′ ) k(\mathbf{w}, \mathbf{w}') k(w,w′) 是协方差函数,用于表示不同参数配置之间的相似性
-
-
更新后验分布:在每次迭代中,根据当前的参数空间和目标函数值,更新高斯过程的后验分布,并基于当前的后验分布生成新的参数选择。贝叶斯调参使用获取函数(Acquisition Function)来选择下一个要评估的参数点。常见的获取函数如期望改进(Expected Improvement, EI)
-
α ( w ) = E [ Δ f ( w ) ] = E [ max ( 0 , f ( w best ) − f ( w ) ) ] \alpha(\mathbf{w}) = \mathbb{E}[ \Delta f(\mathbf{w}) ] = \mathbb{E}[ \max(0, f(\mathbf{w}_{\text{best}}) - f(\mathbf{w})) ] α(w)=E[Δf(w)]=E[max(0,f(wbest)−f(w))]
-
f ( w best ) f(\mathbf{w}_{\text{best}}) f(wbest) 是当前最好的目标函数值
-
Δ f ( w ) \Delta f(\mathbf{w}) Δf(w) 是期望的改进
-
-
选择下一个评估点:通过最大化获取函数来决定下一个评估点。获取函数根据当前的后验分布选择一个最有可能提升目标函数值的参数组合,从而进行下一轮评估
- w ∗ = arg max w α ( w ) \mathbf{w}^*=\arg \max _{\mathbf{w}} \alpha(\mathbf{w}) w∗=argwmaxα(w)
-
重复迭代:贝叶斯优化会根据每一轮评估的结果,调整先验分布,不断优化目标函数,最终找到全局最优的参数配置
- p ( f ( w ) ∣ w ∗ , f ( w ∗ ) ) ∼ G P ( μ ( w ) , Σ ( w ) ) p(f(\mathbf{w})\mid\mathbf{w}^{*},f(\mathbf{w}^{*}))\sim{\mathcal{G}}{\mathcal{P}}({\mu}(\mathbf{w}),\Sigma(\mathbf{w})) p(f(w)∣w∗,f(w∗))∼GP(μ(w),Σ(w))
最终,贝叶斯优化会返回最优的参数 w ∗ \mathbf{w}^* w∗。
此外,除了参数为各通道的权重,对于每篇文档的综合打分(Query-Doc相关性、Doc质量、Doc时效性等分数)的融合公式的权重参数也可以采用贝叶斯优化的方式设定,以此通过对Doc打分实现排序。
总结
在召回模块中,各召回通道通常会通过不同的算法、模型或策略获取候选文档。由于这些召回通道目标、算法和策略的差异,它们生成的候选项通常具有不同的质量和覆盖面。召回聚合的任务是将这些候选项通过一定的方式进行加权、排序和融合,动态控制各个通道的召回量配额,确保最终的候选集合既具有足够的多样性,又能保持较高的相关性。
参考文献
- Reciprocal Rank Fusion outperforms Condorcet and individual Rank Learning Methods
- Practical Bayesian Optimization of Machine Learning Algorithms
相关文章:

搜索召回:召回聚合
召回聚合 用户的查询意图往往是复杂多样的,可能涉及到不同的领域、主题和语义层面。因此,召回体系中通常通过多路召回的方式从不同角度去理解和满足用户的查询需求。此外,多路召回通过各召回通道并行计算可以在海量数据中能够快速响应&#…...

NTFS 文件搜索库
NTFS 文件搜索库 中文 | English 一个快速搜索NTFS卷文件的库 在这里插入图片描述 特性 快速扫描 NTFS 格式驱动器上的所有文件实时快速同步文件变更(创建, 更名, 删除)支持通配符查询文件名或文件路径重启自动更新文件变动, 无需重新进行全盘扫描 API描述 初始化并指定…...
)
【GoF23种设计模式】02_单例模式(Singleton Pattern)
文章目录 前言一、什么是单例模式?二、为什么要用单例模式?三、如何实现单例模式?总结 前言 提示:设计者模式有利于提高开发者的编程效率和代码质量: GoF(Gang of Four,四人帮)设计…...

UniApp:uni-segmented-control 自定义布局
自定义tabs选项,items 为tabs名称数组,横向滚动 <scroll-view scroll-x><view class"segmented-control"><view v-for"(item, index) in items" :key"index" class"control-item ":class"…...

【算法day17-day18】回溯:解决组合问题
不好意思呀各位,最近在忙期末考今天才彻底结束,来让我们继续算法之路吧~ 题目引用 组合电话号码的字母组合组合总和组合总和II分割回文串 1.组合 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回…...

从监控异常发现网络安全
前言 最近在前端异常监控系统中,发现一些异常信息,从中做了一些分析,得到一些体会,因此作文。 发现异常 某天早上打开监控系统发现,当天凌晨1点过测试环境有2个前端上报的异常,报错的原因都是由于没有获取…...
Qt之自定义标题栏拓展(十)
Qt开发 系列文章 - user-defined-titlebars(十) 目录 前言 一、方式一 1.效果演示 2.创建标题栏类 3.可视化UI设计 4.定义相关函数 5.使用标题栏类 二、方式二 1.效果演示 2.创建标题栏类 3.定义相关函数 1.初始化函数 2.功能函数 3.窗口关…...

Verilog中initial的用法
在 Verilog 语言中,initial 语句用于在仿真开始时执行一次性初始化操作。它是顺序执行的,用来描述在仿真启动时立即运行的代码块,通常用于赋初值、生成波形或控制信号行为。 语法 initial begin // 语句1 // 语句2 ... end特点 只…...

(14)D-FINE网络,爆锤yolo系列
yolo过时了?传统的yolo算法在小目标检测方面总是不行,最新算法DEIM爆锤yolo,已经替yolo解决。 一、创新点 这个算法名为DEIM,全称是DETR with Improved Matching for Fast Convergence,其主要创新点在于提出了一…...

Python :冬至快乐
第1部分:基础设置 首先创建一个新的 Python 文件,命名为 fireworks.py。 步骤 1.1: 导入必要的库 import pygame import random import sys from pygame.locals import * import math import time这些库的作用: pygame: 用于创建游戏和图…...
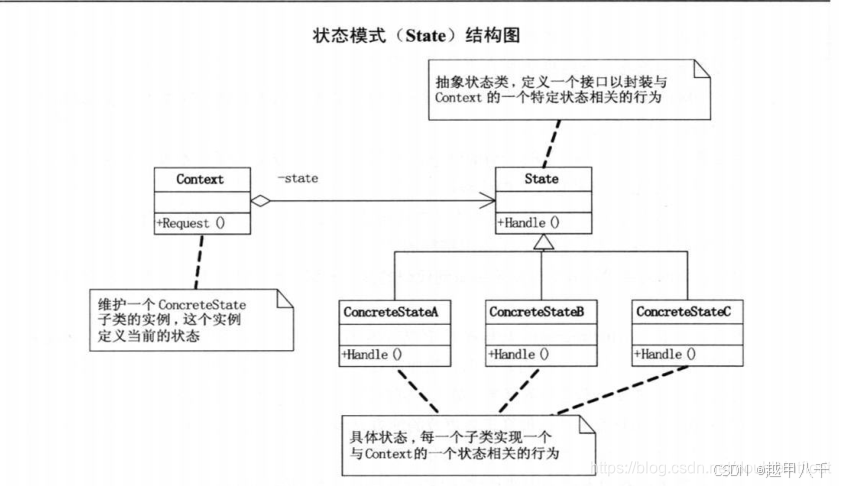
重拾设计模式--状态模式
文章目录 状态模式(State Pattern)概述状态模式UML图作用:状态模式的结构环境(Context)类:抽象状态(State)类:具体状态(Concrete State)类&#x…...
稀疏矩阵的存储与计算 gaxpy
1, gaxpy 数学公式 其中: , , 2, 具体实例 3,用稠密矩阵的方法 本节将用于验证第4节中的稀疏计算的结果 hello_gaxpy_dense.cpp #include <stdio.h> #include <stdlib.h>struct Matrix_SP {float* val; //…...
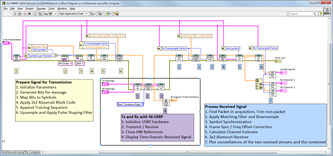
基于LabVIEW的USRP信道测量开发
随着无线通信技术的不断发展,基于软件无线电的设备(如USRP)在信道测量、无线通信测试等领域扮演着重要角色。通过LabVIEW与USRP的结合,开发者可以实现信号生成、接收及信道估计等功能。尽管LabVIEW提供了丰富的信号处理工具和图形…...
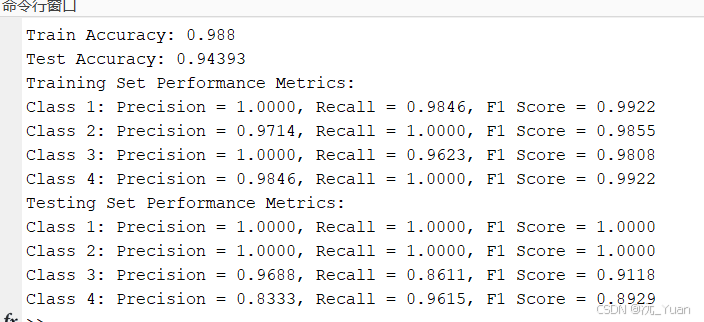
基于LSTM长短期记忆神经网络的多分类预测【MATLAB】
在深度学习中,长短期记忆网络(LSTM, Long Short-Term Memory)是一种强大的循环神经网络(RNN)变体,专门为解决序列数据中的长距离依赖问题而设计。LSTM因其强大的记忆能力,广泛应用于自然语言处理…...
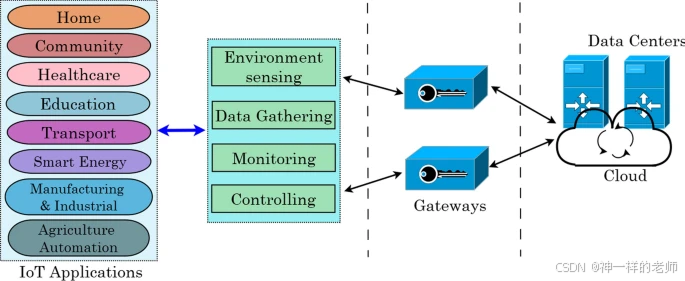
物联网:全面概述、架构、应用、仿真工具、挑战和未来方向
中文论文标题:物联网:全面概述、架构、应用、仿真工具、挑战和未来方向 英文论文标题:Internet of Things: a comprehensive overview, architectures, applications, simulation tools, challenges and future directions 作者信息&#x…...
volatility2工具的使用vol2工具篇
vol2工具 命令格式:vol.py -f [image] --profile[profile] [plugin] 1、查看系统的操作版本,系统镜像信息 2.查看用户名密码信息,当前操作系统中的password hash,例如SAM文件内容 3.从注册表提取LSA密钥信息(已解密&…...

R 基础运算
R 基础运算 R 是一种广泛使用的统计编程语言,它提供了强大的数据操作和分析功能。基础运算在 R 中非常重要,因为它们是进行更复杂计算和数据分析的基础。本文将详细介绍 R 中的基础运算,包括算术运算、逻辑运算、向量化和矩阵运算。 一、算…...
javaScriptBOM
1.1、BOM概述 1.1.1、BOM简介 BOM(browser Object)即浏览器对象模型,它提供了独立于内容而与浏览器窗口进行交互的对象,其核心对象是window。 BOM由一系列的对象构成,并且每个对象都提供了很多方法与属性 BOM缺乏标准…...

Godot RPG 游戏开发指南
Godot RPG 游戏开发指南 一、基础准备 1. 开发环境 下载并安装最新版 Godot 4.x选择使用 GDScript 或 C# 作为开发语言准备基础美术资源(角色、地图、道具等) 2. 项目结构 project/ ├── scenes/ # 场景文件 ├── scripts/ # 脚…...

目标检测数据集图片及标签同步旋转角度
前言 在深度学习领域,尤其是目标检测任务中,数据集的质量直接影响模型的性能。为了提升模型的鲁棒性和对各种场景的适应能力,数据增强技术被广泛应用于图像数据集处理。旋转角度是常见的数据增强方法,通过对图像及其对应的标签&am…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
