【信号滤波 (上)】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++)
目录
- 一、ADC采样的噪声简介
- 1.1 常见的ADC噪声来源
- 二、信号的时域到频域转换
- 2.1 傅里叶变换
- 巧记傅里叶变换
- 三、傅里叶变换和滤波算法工程实现
- 3.1 使用Matlab计算信号时域到频域的变换
- 3.2 使用Matlab去除特定频点噪声
- 寻找峰值算噪声频率
- 构建陷波滤波器滤除噪声频点
- 陷波滤波器与滑动平均滤波器对比
- 3.3 C++ 实现ADC采样信号滤波
一、ADC采样的噪声简介
经常用ADC采样的朋友都知道,采样的数据不是纯净的信号,会伴随着干扰。
一般把周期性的干扰叫噪声,既然是周期性的,一定能算出周期时长T,取倒数就是频率f,单位Hz。
1.1 常见的ADC噪声来源
电源是噪声的一大来源,如果用的是交流电,交流电通过整流电路中的二极管元件,过滤掉交流电的负半周,然后通过滤波电容滤波让交流电趋于平缓,形成直流电。交流信号肯定不能滤干净的,这就是电源纹波产生的一大原因,电源纹波会导致ADC采样信号出现噪声。
二、信号的时域到频域转换
刚接触信号的时候搞不清楚什么是时域什么是频域,大学里的《信号与系统》《控制工程与原理》《信号处理》等书上提过,但因为没有结合实际使用学过都忘记了。
时域可以理解成横轴是时间t,纵轴是其他有幅值变换的物理量(如电压,声响,亮度,温度,振幅等),如下图左图所示;
频域是横轴为频率大小,纵轴为频率分量的强度(或者叫功率密度);
而傅里叶变换就是时域和频域的联结。

2.1 傅里叶变换
从时域变换到频域用的是傅里叶变换,傅里叶觉得计算波形相加和分解太麻烦了,发明了一种简单的方法让波形相加能像“1+1=2”一样直观,他的方法就是把波形从时域转换到频域再相加或者分解,计算好后再转回时域波形。我们把傅里叶发明的这套方法叫做“傅里叶变换”和“傅里叶逆变换”。
公式如下,如果看不懂一是回去复习微积分,二是用我下面的方法巧记:
F ( ω ) = F { f ( t ) } = 1 / 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t ( 傅里叶变换 ) F(\omega) = \mathcal{F}\{f(t)\} ={1/2\pi} \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt (傅里叶变换) F(ω)=F{f(t)}=1/2π∫−∞∞f(t)e−iωtdt(傅里叶变换)
f ( t ) = F − 1 { F ( ω ) } = ∫ − ∞ ∞ F ( ω ) e i ω t d ω ( 傅里叶逆变换 ) f(t) = \mathcal{F}^{-1}\{F(\omega)\} = \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \, d\omega (傅里叶逆变换) f(t)=F−1{F(ω)}=∫−∞∞F(ω)eiωtdω(傅里叶逆变换)
也可以用 ω = 2 π f \omega = 2\pi f ω=2πf带入
F ( f ) = F { f ( t ) } = ∫ − ∞ ∞ f ( t ) e − 2 π i f t d t F(f) = \mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t) e^{-2\pi i f t} \, dt F(f)=F{f(t)}=∫−∞∞f(t)e−2πiftdt
f ( t ) = F − 1 { F ( f ) } = ∫ − ∞ ∞ F ( f ) e 2 π i f t d f f(t) = \mathcal{F}^{-1}\{F(f)\} = \int_{-\infty}^{\infty} F(f) e^{2\pi i f t} \, df f(t)=F−1{F(f)}=∫−∞∞F(f)e2πiftdf
巧记傅里叶变换
先看这个动画
傅里叶变换动画
首先看懂公式最里面的这个 e − i ω t e^{-i \omega t} e−iωt,这其实就是三角函数在复数域的延申。
已知欧拉公式 e − i ω t = c o s ( ω t ) − i s i n ( ω t ) e^{-i \omega t}=cos(\omega t)-isin(\omega t) e−iωt=cos(ωt)−isin(ωt), e − i ω t e^{-i \omega t} e−iωt可以看成一个距离原地1单位的球在绕着原点以 ω \omega ω角速度旋转,从x轴(实数)看过去就是 c o s ( ω t ) cos(\omega t) cos(ωt),从y轴(虚数)看过去就是 s i n ( ω t ) sin(\omega t) sin(ωt)。



然后再看 f ( t ) e − i ω t f(t) e^{-i \omega t} f(t)e−iωt,下面动图最上面的蓝线是时域函数f(t),红线就是 e − i ω t e^{-i \omega t} e−iωt的实数轴部分,这里有两个变量 ω \omega ω和t把大家看懵了,我们细细捋一下,下面的横轴就是t,t从(0,∞)的变换都已经显示在数轴上了,可以看成静态量,导致红线变化的是另一个变量 ω \omega ω,它才是动态变量。
f ( t ) e − i ω t f(t) e^{-i \omega t} f(t)e−iωt也就是把 f ( t ) f(t) f(t)和 e − i ω t e^{-i \omega t} e−iωt相乘,也就是中间图。可以看到当 e − i ω t e^{-i \omega t} e−iωt变化的和 f ( t ) f(t) f(t)波动频率一致的时候,乘积结果就是 s i n 2 ( t ) = ( 1 − c o s ( 2 t ) ) / 2 sin^2(t) = {(1-cos(2t))}/2 sin2(t)=(1−cos(2t))/2。
最后经过积分, ∫ − ∞ ∞ f ( t ) e − i ω t d t \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt ∫−∞∞f(t)e−iωtdt得到的下图。注意看,这是对时间t进行积分,之前说过时间是静态量,所以图中横轴已经不是时间t了,而是角频率 ω \omega ω,公式 F ( ω ) = 1 / 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t F(\omega) ={1/2\pi} \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt F(ω)=1/2π∫−∞∞f(t)e−iωtdt表示的是积分结果随着频率变化而变化。
最后一张图和时间已经没关系了,横轴已经是频率了,这样就完成了时域到频域的转化。
PS:为啥要费劲心思把周期信号从时域转频域,关键就是"周期",周期意味着经过一定时间后会重复,所以时间反而不重要了,重要的是频率。下图的最高点对应的就是原始信号的频率。
(动图参考来源:https://blog.csdn.net/YuHWEI/article/details/136678900)

上面的图能解释傅里叶变换但不是真正的傅里叶变换,因为我们只计算了实数轴,真正的傅里叶变换后,正弦信号是在8.3Hz上的一道冲击信号。

同理,多个周期性正弦波叠加也可以从频域上看出频率分量。
在频域上做周期性信号的合成与分解是不是就简单多了呢。

通过不同频率的正弦波叠加,想要什么波形都能叠加出来。
反过来,任何一种波形,都可以分解成不同频率的正弦波叠加。

三、傅里叶变换和滤波算法工程实现
3.1 使用Matlab计算信号时域到频域的变换
matlab使用快速傅里叶变换函数(fft),注意fft后的复数域的量,还需要abs()一下才能显示到实数轴上。
data = xlsread('origin_signal_data.xlsx'); % 读取原始波形数据
voltage = data(:, 1); N = length(voltage); % 数据长度t = 2.5; %总采样时间
T = t/N; %采样周期=总采样时间/总采样次数
Fs = 1/T; %采样率是1s内的采样次数
time = 0:5:2500-5; %设置横坐标数组
plot(time, voltage, 'r', 'LineWidth', 2); % 绘制单边频谱的幅值谱
xlabel('采样时间 (ms)'); % 频率轴标签(需要知道采样率才能正确标注)
ylabel('电压 (mV)'); % 幅值轴标签
title('原始时域波形'); % 图表标题
grid on;% data_no_dc = timeSeries - signal_mean;
Y = fft(voltage); % 计算FFT
P2 = abs(Y/N); % 双边频谱的幅值,并归一化
P1 = P2(1:N/2+1); % 单边频谱的幅值(正频率部分)
P1(2:end-1) = 2*P1(2:end-1); % 因为FFT结果是对称的,所以正频率部分的幅值要乘以2(除了第一个和最后一个点)f = (0:N-1)*(1/N); % 频率向量(归一化频率)
f_actual = f*(Fs); % 实际频率(需要知道采样率)
f_used = f_actual(1:N/2+1); %使用到的只有一半plot(f_used, P1); % 绘制单边频谱的幅值谱
xlabel('频率 (Hz)'); % 频率轴标签(需要知道采样率才能正确标注)
ylabel('幅值');
title('傅里叶变换后频域波形'); % 图表标题
grid on; % 显示网格
下面左图的原始数据中还有周期性噪声干扰,通过傅里叶变换后看到噪声主要集中在60Hz。
注意!我这里是去除了0Hz的数据,0Hz是信号中的直流分量,信号都是直流分量和交流分量的叠加,如果傅里叶变换后0Hz有很高的幅值,那就是直流分量,我们要处理的是噪声肯定是交流分量,所以作图时不要把0Hz算进去。

3.2 使用Matlab去除特定频点噪声
寻找峰值算噪声频率
ignore_below_frequency = 1; % 1Hz以下不管,因为是信号的直流分量% 寻找傅里叶变换后最大幅值所在的频点
validIndices = f_used >= ignore_below_frequency;
filteredP1 = P1(validIndices);
filteredF = f_used(validIndices); [peakAmplitude, peakIndex] = max(filteredP1);
peakFrequency = filteredF(peakIndex); % 获得噪声频率
构建陷波滤波器滤除噪声频点
构建陷波滤波器,设置滤波频点和带宽
% 设置60Hz陷波滤波器
wo = peakFrequency / (Fs / 2);
bw = wo / 20; % 设置滤波器带宽
notchFilter = designfilt('bandstopiir', ...'FilterOrder', 2, ...'HalfPowerFrequency1', wo - bw/2, ...'HalfPowerFrequency2', wo + bw/2, ...'DesignMethod', 'butter');% 使用滤波器
filtered_voltage = filtfilt(notchFilter, voltage);
陷波滤波器与滑动平均滤波器对比
滑动平均滤波器就是设置一个窗口,窗口内包含多个采样频点,比如前7个数据为一个窗口,取窗口内数据的平均值为当前点的值,然后窗口向后滑动,滑动平均算法的核心思想是在一个正弦周期内所有点之和为零。
如果选的窗口刚好是噪声周期,那就滤除干扰了。
但滑动平均在较低频率下好用,高频后窗口大小无法继续缩小,不如陷波滤波。

3.3 C++ 实现ADC采样信号滤波
matlab验证方法,工程实现还是要用C++,这里我要把算法最终应用到嵌入式设备上去,所以使用QT的C++来部署验证。
QT C++需要使用快速傅里叶变换库和矩阵库支持
在.pro文件里加入fftw3库。
LIBS += -lfftw3
同时下载Eigen库放到项目文件中,并加入头文件路径
INCLUDEPATH += ./eigen-3.4.0
陷波滤波器没有现场的库,需要手动写
QVector<double> applyNotchFilter(const QVector<double> &voltageData, double sampleRate, double notchFreq, double qualityFactor)
{QVector<double> filteredData(voltageData.size());double w0 = 2.0 * M_PI * notchFreq / sampleRate;double alpha = sin(w0) / (2.0 * qualityFactor);double b0 = 1.0;double b1 = -2.0 * cos(w0);double b2 = 1.0;double a0 = 1.0 + alpha;double a1 = -2.0 * cos(w0);double a2 = 1.0 - alpha;b0 /= a0;b1 /= a0;b2 /= a0;a1 /= a0;a2 /= a0;double x1 = 0.0, x2 = 0.0; double y1 = 0.0, y2 = 0.0; for (int i = 0; i < voltageData.size(); ++i) {double x0 = voltageData[i];double y0 = b0 * x0 + b1 * x1 + b2 * x2 - a1 * y1 - a2 * y2;filteredData[i] = y0;x2 = x1;x1 = x0;y2 = y1;y1 = y0;}return filteredData;
}
为了像matlab一样能直观的看到滤波效果,用QChart作图
void displayFilterResult(const QVector<double> timeData, const QVector<double> &voltageData, const QVector<double> filteredData, const double maxFrequency)
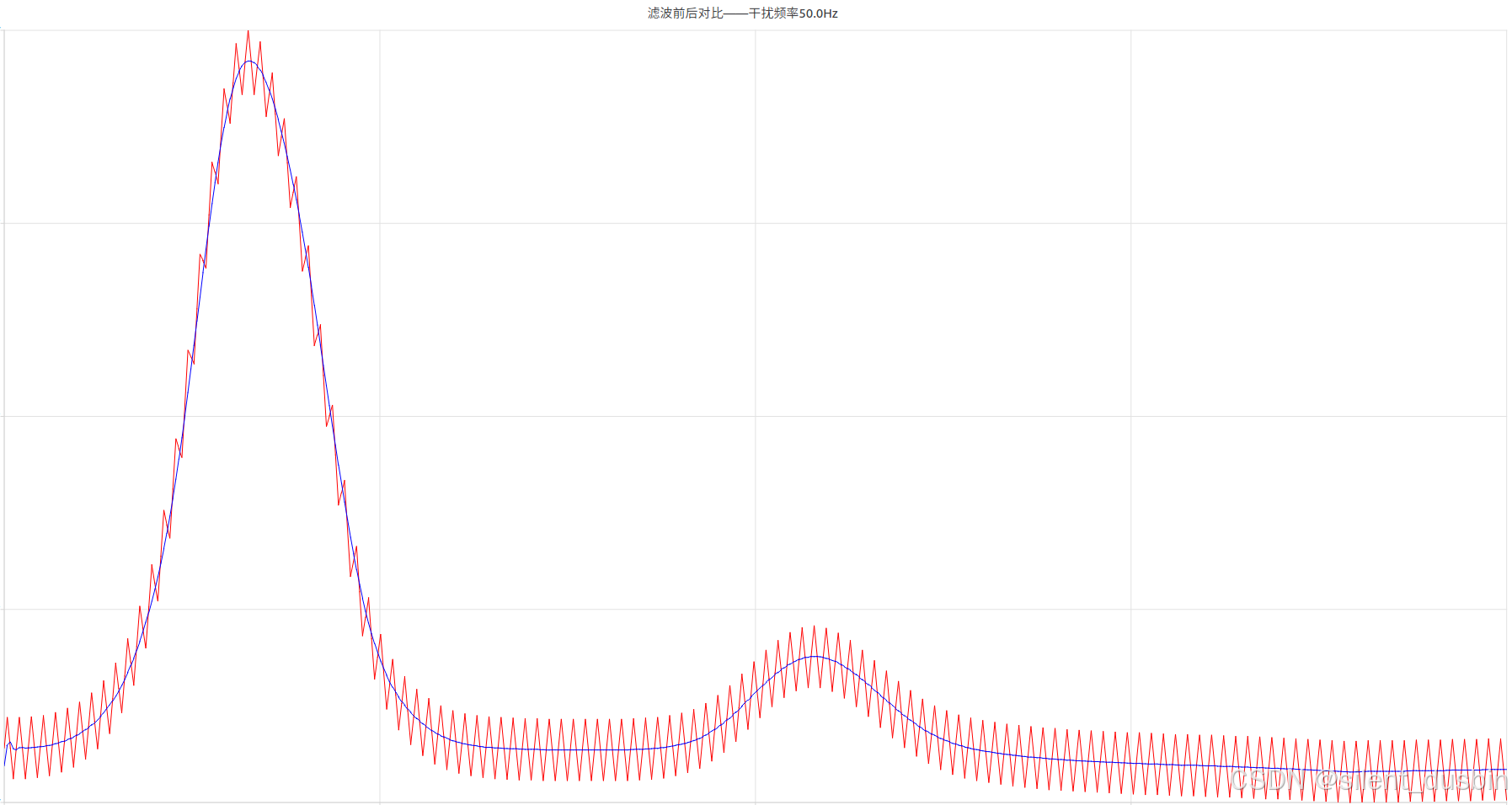
{// 创建QLineSeries对象,并设置它们的名称QLineSeries *seriesVoltage = new QLineSeries();seriesVoltage->setName("原始电压数据"); // 设置名称为“原始电压数据”QLineSeries *seriesFiltered = new QLineSeries();seriesFiltered->setName("滤波后电压数据"); // 设置名称为“滤波后电压数据”// 填充数据到QLineSeries对象for (int i = 0; i < timeData.size(); ++i) {seriesVoltage->append(timeData[i], voltageData[i]);seriesFiltered->append(timeData[i], filteredData[i]);}// 创建QChart对象,并添加系列(与之前相同)QChart *chart = new QChart();chart->addSeries(seriesVoltage);chart->addSeries(seriesFiltered);// 默认情况下,图例是可见的,但你可以通过以下方式访问和配置它QLegend *legend = chart->legend();legend->setVisible(true); // 通常情况下这是默认的,但你可以显式设置legend->setAlignment(Qt::AlignBottom); // 设置图例的位置,这里是在底部// 为图表设置标题(与之前相同)QString frequency = QString::number(maxFrequency, 'f', 1) + "Hz";chart->setTitle("滤波前后对比——干扰频率" + frequency);// 创建QValueAxis对象并设置轴的范围QValueAxis *axisX = new QValueAxis();axisX->setLabelFormat("%g s");chart->addAxis(axisX, Qt::AlignBottom);seriesVoltage->attachAxis(axisX);seriesFiltered->attachAxis(axisX);QValueAxis *axisY = new QValueAxis();axisY->setLabelFormat("%g V");chart->addAxis(axisY, Qt::AlignLeft);seriesVoltage->attachAxis(axisY);seriesFiltered->attachAxis(axisY);// 为不同的系列设置不同的颜色seriesVoltage->setPen(QPen(QColor(255, 0, 0))); // 红色seriesFiltered->setPen(QPen(QColor(0, 0, 255))); // 蓝色// 创建QChartView对象并设置QChartQChartView *chartView = new QChartView(chart);chartView->setRenderHint(QPainter::Antialiasing);// 创建主窗口并显示图表QMainWindow* window = new QMainWindow();window->setCentralWidget(chartView);window->resize(1920, 1080);window->show();
}
主函数如下
#include <QFile>
#include <QString>
#include <QVector>
#include <QDebug>
#include <QtCharts/QChartView>
#include <QtCharts/QLineSeries>
#include <QtCharts/QValueAxis>
#include <QMainWindow>
#include <QApplication>#include <fftw3.h>
#include <Eigen/Dense>using namespace Eigen;
using namespace std;QT_CHARTS_USE_NAMESPACEint main(int argc, char *argv[]) {QApplication a(argc, argv);QFile inputFile("./source_signal_data.csv");if (!inputFile.open(QIODevice::ReadOnly | QIODevice::Text)) {qDebug() << "文件打开失败";return -1;}QVector<double> voltageData;while (!inputFile.atEnd()) {QByteArray line = inputFile.readLine();voltageData.push_back(line.toDouble());}inputFile.close();// 配置周期和频率int N = voltageData.size();double t = 2.5; // 总时间double T = t / N;double Fs = 1 / T; // 采样频率// 生成时间数据,从0s开始,每隔0.005s到2.5sQVector<double> timeData;for (double t = 0; t < (2.5 - 0.005); t += 0.005) {timeData.append(t);}// 将信号数据放到实部中VectorXd voltageEigen(N);for (int i = 0; i < N; ++i) {voltageEigen[i] = voltageData[i];}fftw_complex* in = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * N);fftw_complex* out = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * N);fftw_plan plan = fftw_plan_dft_1d(N, in, out, FFTW_FORWARD, FFTW_ESTIMATE);for (int i = 0; i < N; i++) {in[i][0] = voltageEigen[i]; // 实部in[i][1] = 0.0; // 虚部}fftw_execute(plan); //应用傅里叶变换VectorXcd fftResult(N);for (int i = 0; i < N; i++) {fftResult[i] = std::complex<double>(out[i][0], out[i][1]);}// 清楚缓存fftw_destroy_plan(plan);fftw_free(in);fftw_free(out);// 制作频谱VectorXd absFFT = fftResult.cwiseAbs() / N;VectorXd P1 = absFFT.head(N / 2 + 1);P1.segment(1, P1.size() - 2) *= 2;VectorXd f_actual = VectorXd::LinSpaced(N / 2 + 1, 0, Fs / 2);// 滤除直流分量QVector<double> filteredP1;QVector<double> filteredF;for (int i = 0; i < f_actual.size(); ++i) {if (f_actual(i) >= 1) {filteredP1.push_back(P1(i));filteredF.push_back(f_actual(i));}}// 导出到csvQFile outputFile("../FFT_test/filtered_data.csv");if (outputFile.open(QIODevice::WriteOnly | QIODevice::Text)) {QTextStream out(&outputFile);out << "频率,幅值\n";for (int i = 0; i < filteredF.size(); ++i) {out << filteredF[i] << "," << filteredP1[i] << "\n";}outputFile.close();} else {qDebug() << "导出失败" ;}// 寻找噪声最大的幅值和对应的频率auto maxIt = max_element(filteredP1.begin(), filteredP1.end());double maxAmplitude = 0.0;double maxFrequency = 0.0;if (maxIt != filteredP1.end()){size_t maxIndex = distance(filteredP1.begin(), maxIt);maxAmplitude = *maxIt;maxFrequency = filteredF[maxIndex];}else{qDebug() << "未找到噪声频率";}double qualityFactor = 1; // 设置陷波滤波带宽QVector<double> filteredData = applyNotchFilter(voltageData, Fs, maxFrequency, qualityFactor);// 导出到csvQString notchFileName = "./notch_filtered_" + QString::number(maxFrequency, 'f', 1) + "Hz.csv";QFile notchOutputFile(notchFileName);if (notchOutputFile.open(QIODevice::WriteOnly | QIODevice::Text)) {QTextStream out(¬chOutputFile);for (int i = 0; i < filteredData.size(); ++i) {out << filteredData[i] << "\n";}notchOutputFile.close();} else {qDebug() << "导出失败";}//在图表上显示滤波前后效果displayFilterResult(timeData, voltageData, filteredData, maxFrequency);return a.exec();
}
QT滤波实现效果如下:
相关文章:

【信号滤波 (上)】傅里叶变换和滤波算法去除ADC采样中的噪声(Matlab/C++)
目录 一、ADC采样的噪声简介1.1 常见的ADC噪声来源 二、信号的时域到频域转换2.1 傅里叶变换巧记傅里叶变换 三、傅里叶变换和滤波算法工程实现3.1 使用Matlab计算信号时域到频域的变换3.2 使用Matlab去除特定频点噪声寻找峰值算噪声频率构建陷波滤波器滤除噪声频点陷波滤波器与…...

Idea内,光标显示问题
键盘误触导致光标显示为白色块 解决方式 任选其一 键盘敲击 Ins 键(既 insert 键)Shift 0(数字零)...

回顾 python3中字符串
一. 简介 前面学习了 python3中的字符串, 本文回顾一下 python3中的字符串。 二. python3中的字符串 1. 创建字符串 字符串是 python中最常用的数据类型。我们可以使用引号( 或者 " )来创建字符串。 创建字符串很简单,…...

代码随想录day23 | leetcode 39.组合总和 40.组合总和II 131.分割回文串
39.组合总和 Java class Solution { List<List<Integer>> result new ArrayList<>();LinkedList<Integer> path new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sor…...
备考实战之分支结构(switch语句))
全国青少年信息学奥林匹克竞赛(信奥赛)备考实战之分支结构(switch语句)
if语句处理多个分支时需要用if-else if结构,分支越多,嵌套的if语句层就越多,程序不但庞大、复杂,理解起来也比较困难。在C编程中,针对有些问题除了使用if-else if结构之外,还有switch语句也可以实现&#x…...

R机器学习:决策树算法的理解与实操
今天继续给大家介绍决策树算法,决策树本身是一种非常简单直观的机器学习算法,用于做分类或回归任务。它就像我们平常做决定时的过程,通过逐步排除可能的选项,最终得出结论。 A decision tree is a flowchart-like structure used …...

解锁高效学习之道:从认知升级到实践突破
目录 学习之困:探寻低效的根源 (一)迷茫之境:目标缺失的困扰 (二)表象之迷:浅尝辄止的学习 (三)行动之阻:执行力的短板 认知重塑:明晰学习的本…...

2024年12月CCF-GESP编程能力等级认证Python编程三级真题解析
本文收录于专栏《Python等级认证CCF-GESP真题解析》,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 一、单选题(每题 2 分,共 30 分) 第 1 题 2024年10月8日,诺贝尔物理学奖“意外地”颁给了两位计算机科学家约翰霍普菲尔德(John J. Hopfield)和杰弗里辛顿(Geof…...

.NET Core 中使用 C# 获取Windows 和 Linux 环境兼容路径合并
在 .NET Core 中使用 C# 处理路径合并并确保在 Windows 和 Linux 环境中都能正常工作,可以使用 System.IO.Path 和 System.IO.Path.Combine 方法。它们是跨平台的,能够根据操作系统自动处理路径分隔符。可以通过 System.Runtime.InteropServices.Runtime…...
【SH】Ubuntu Server 24服务器搭建MySQL数据库研发笔记
文章目录 搭建服务器在线安装1. 更新软件包列表2. 安装MySQL3. 检查MySQL状态4. 修改密码5. 新增用户6. 设置局域网访问 离线安装下载安装包 常用命令参考文档在线安装日志 搭建服务器 作者羊大侠搭建的是 Ubuntu Server 24.04 LTS 服务器环境 搭建参考文档:【SH】…...
编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。 1. 正则表达式 正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式…...
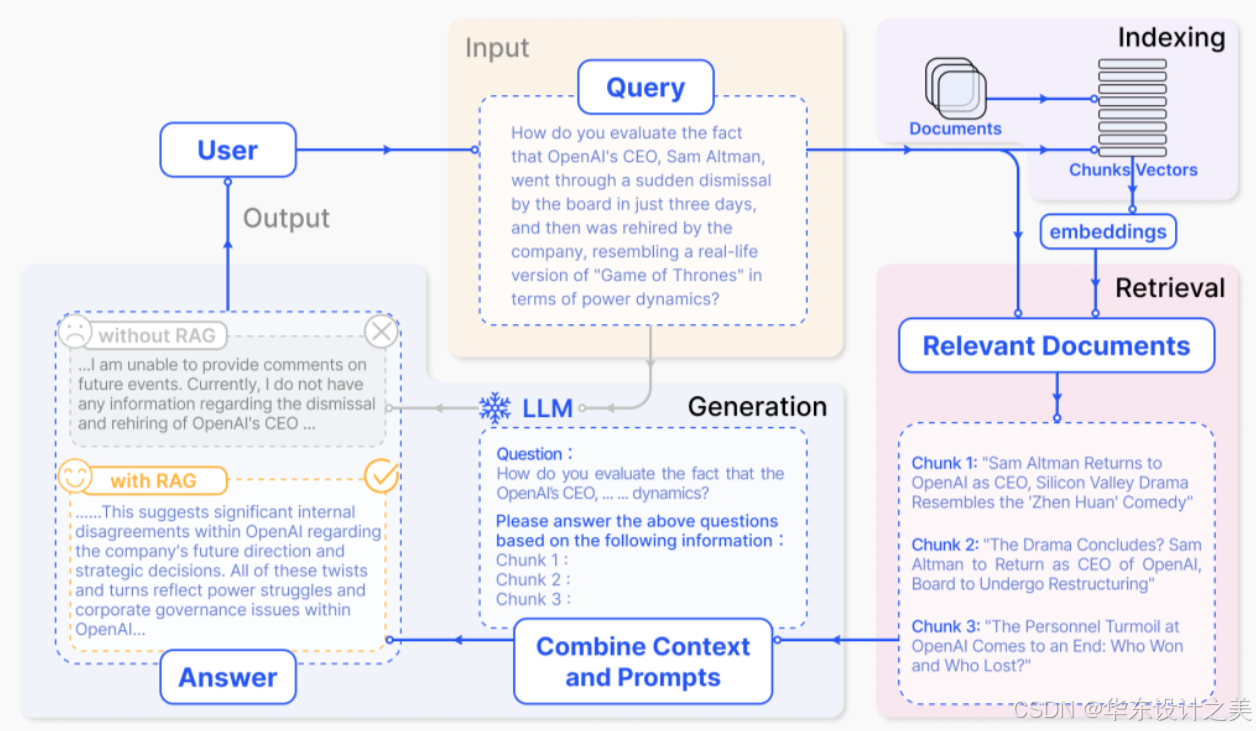
知识图谱+RAG学习
GraphRAG(Graph-based Retrieval-Augmented Generation)是微软在2024年推出的一项开源技术,旨在通过结合知识图谱和检索增强生成(RAG)方法,为大型语言模型(LLM)的数据处理提供全新解…...
消息队列技术的发展历史
消息队列技术的演进历程宛如一幅波澜壮阔的科技画卷,历经多个标志性阶段,各阶段紧密贴合不同的技术需求与市场风向,下面为您详细道来。 第一阶段:消息中间件的起源(1970 年代末期 - 1980 年代中期) 在计算…...

每天40分玩转Django:Django部署
Django部署 一、今日学习内容概述 学习模块重要程度主要内容生产环境配置⭐⭐⭐⭐⭐settings配置、环境变量WSGI服务器⭐⭐⭐⭐⭐Gunicorn配置、性能优化Nginx配置⭐⭐⭐⭐反向代理、静态文件安全设置⭐⭐⭐⭐⭐SSL证书、安全选项 二、生产环境配置 2.1 项目结构调整 mypr…...
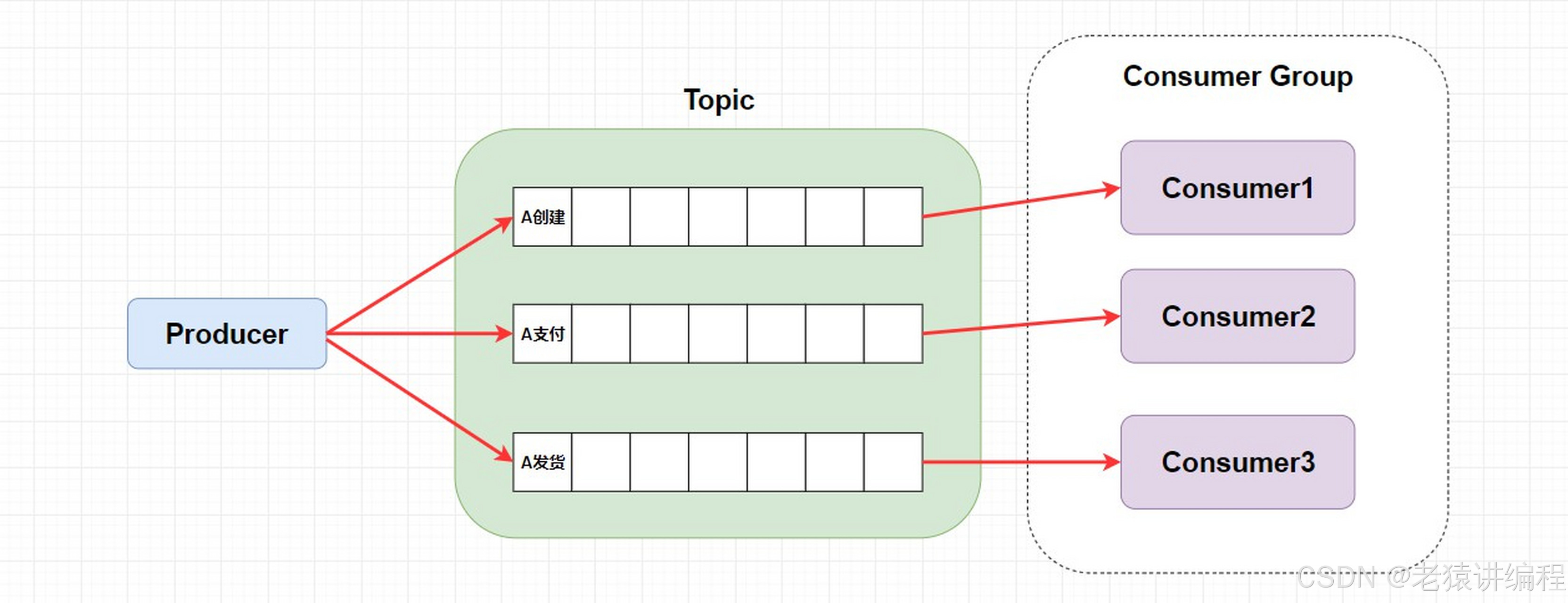
搭建Elastic search群集
一、实验环境 二、实验步骤 Elasticsearch 是一个分布式、高扩展、高实时的搜索与数据分析引擎Elasticsearch目录文件: /etc/elasticsearch/elasticsearch.yml#配置文件 /etc/elasticsearch/jvm.options#java虚拟机 /etc/init.d/elasticsearch#服务启动脚本 /e…...
解析 Ingress-Nginx 故障:排查思路与方法
文章目录 一、什么是Ingress-Nginx二、故障排除1.1Ingress-Controller日志和事件检查 Ingress 资源事件检查 Nginx 配置检查使用的服务是否存在调试日志 1.2对 Kubernetes API 服务器的认证服务认证服务账户Kube-Config 1.3使用GDB和Nginx1.4在 Nginx 4.2.5 或其他版本…...

2024 楚慧杯 re wp
go_bytes 附件拖入ida 输入长度为0x28,每两位字符的4bit拼接 与一个常量值经过运算后的值进行异或,并且判断是否相等 脚本 bouquet 附件拖入ida。简单去一下花 构建了一个二叉树,然后递归调用函数 重新排列一下再层序遍历读出即可 zistel 附件…...

【物联网技术与应用】实验10:蜂鸣器实验
实验10 蜂鸣器实验 【实验介绍】 蜂鸣器是音频信号装置。蜂鸣器可分为有源蜂鸣器和无源蜂鸣器。 【实验组件】 ● Arduino Uno主板* 1 ● USB数据线* 1 ● 有源蜂鸣器* 1 ● 无源蜂鸣器* 1 ● 面包板* 1 ● 9V方型电池* 1 ● 跳线若干 【实验原理】 如图所示&#x…...
)
单片机:实现矩阵键盘控制LCD屏幕(附带源码)
单片机实现矩阵键盘控制LCD屏幕 矩阵键盘(Matrix Keypad)是一种常用的输入设备,广泛应用于嵌入式系统中。在许多嵌入式应用中,我们常常需要通过按键输入来控制系统的功能。结合LCD显示屏,我们可以实现一个简单的界面&…...

鸿蒙Next之包体积极限优化
鸿蒙应用包大小优化全解析 在鸿蒙应用开发中,减小应用包大小对于提升应用下载和安装体验起着关键作用。通过压缩、精简或复用应用中的代码与资源,能有效降低包体积,减少空间占用并加快下载与安装速度。下面详细介绍一下鸿蒙应用包大小优化的…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
