No. 34 笔记 | Python知识架构与数据类型相关内容 | 实操
在今天的Python学习中,我对Python的知识架构有了更深入的理解,同时也对Python的数据类型及其操作有了全面的认识和实践。
一、Python知识架构理解

Python是一门功能强大且应用广泛的编程语言,其知识架构可以从多个层面来理解。
从整体结构上看,Python程序由模块组成,模块是组织代码的基本单位,它将相关的功能和代码封装在一起,便于管理和复用。模块中包含语句,语句是执行具体操作的指令,比如变量赋值、函数调用等。而语句又由表达式构成,表达式是产生值或结果的代码片段,例如数值运算、逻辑判断等。
从语言特性方面来说,Python具有简洁清晰的语法,使得代码易于编写和阅读。它支持多种编程范式,包括面向过程、面向对象和函数式编程,这使得开发者可以根据不同的需求和场景选择合适的编程方式。Python还拥有丰富的标准库和第三方库,涵盖了从文件操作、网络通信到数据分析、机器学习等众多领域,极大地提高了开发效率,降低了开发难度。
此外,Python的解释型特性使得代码可以在不同的平台上快速运行和调试,无需进行复杂的编译过程。其动态类型系统允许变量在运行时根据赋值的对象自动确定类型,这在一定程度上增加了代码的灵活性,但也需要开发者在编写代码时更加注意类型相关的问题,以避免潜在的错误。
二、Python的数据类型及操作
Python的数据类型丰富多样,每种类型都有其独特的特点和用途,以下是详细介绍及相关操作:
(一)数值类型
Python的数值类型主要包括整数(int)和浮点数(float)。
- 四则运算:
- 加法:例如
3 + 5,结果为8。 - 减法:
7 - 2,结果是5。 - 乘法:
4 * 6,得到24。 - 除法:
9 / 3,结果为3.0(在Python 3中,整数除法默认返回浮点数)。 - 取整除法:
9 // 3,结果为3,只取商的整数部分。 - 取余运算:
10 % 3,结果是1,即10除以3的余数。 - 幂运算:
2 ** 3,表示2的3次方,结果为8。

- 加法:例如
(二)列表(List)
列表是Python中常用的有序集合,可以包含不同类型的元素,并且元素可以修改。
- 索引访问:
-
正向索引:从0开始,例如
my_list = [10, 20, 30, 40],my_list[0]获取到第一个元素10,my_list[2]获取到第三个元素30。

-
反向索引:从-1开始,
my_list[-1]获取到最后一个元素40,my_list[-2]获取到倒数第二个元素30。
-

- 高级语法操作:
-
切片:
my_list[1:3]获取从索引1(包含)到索引3(不包含)的子列表,即[20, 30]。my_list[:3]表示从开头到索引3(不包含),结果为[10, 20, 30],my_list[2:]表示从索引2(包含)到末尾,结果是[30, 40]。

-
列表推导式:例如
[i ** 2 for i in range(5)],会生成一个包含0到4的平方数的列表[0, 1, 4, 9, 16]。
-

- 添加元素:`my_list.append(50)`,在列表末尾添加元素`50`。`my_list.insert(2, 25)`,在索引2的位置插入元素`25`。

- 删除元素:`my_list.remove(30)`,删除列表中第一个值为`30`的元素。`del my_list[1]`,删除索引为1的元素。

(三)元组(Tuple)
元组与列表类似,但元素不可修改,一旦创建,其内容就不能改变。
-
索引访问:
- 同样支持正向和反向索引,例如
my_tuple = (100, 200, 300),my_tuple[0]获取到100,my_tuple[-1]获取到300。

- 同样支持正向和反向索引,例如
-
高级语法操作:
-

-
虽然元组本身不可变,但如果元组中的元素是可变类型(如列表),则可以修改该可变元素。例如
my_tuple = (100, [200, 300], 400),可以通过my_tuple[1].append(500)来修改元组中列表元素的值,此时元组变为(100, [200, 300, 500], 400),但元组的结构(元素个数和位置)并未改变。 -
元组也支持切片操作,用法与列表相同,如
my_tuple[1:3]。
-
(四)字典(Dictionary)
字典是一种无序的键值对集合,通过键(key)来访问值(value),键必须是唯一的,而值可以重复。
# 字典的创建和键访问
my_dict = {'name': 'Alice', 'age': 25, 'city': 'New York'}
print(my_dict['name'])
print(my_dict['age']) # 添加键值对
my_dict['gender'] = 'female'
print(my_dict) # 修改值
my_dict['age'] = 26
print(my_dict) # 删除键值对
del my_dict['city']
print(my_dict) # 遍历字典的键
for key in my_dict.keys():print(key)# 遍历字典的值
for value in my_dict.values():print(value)# 遍历字典的键值对
for key, value in my_dict.items():print(key, value)
-
key访问:
- 例如
my_dict = {'name': 'Alice', 'age': 25, 'city': 'New York'},通过my_dict['name']可以获取到值'Alice',my_dict['age']获取到25。
- 例如
-
高级语法操作:
- 添加键值对:
my_dict['gender'] = 'female',向字典中添加一个新的键值对。 - 修改值:
my_dict['age'] = 26,将age对应的值修改为26。 - 删除键值对:
del my_dict['city'],删除指定键的键值对。 - 遍历字典:
- 遍历键:
for key in my_dict.keys(): print(key),会依次输出字典的所有键。 - 遍历值:
for value in my_dict.values(): print(value),会依次输出字典的所有值。 - 遍历键值对:
for key, value in my_dict.items(): print(key, value),会依次输出字典的每个键值对。
- 遍历键:
- 添加键值对:

三、列表、元组、字典的区分
列表、元组和字典虽然都用于存储数据,但它们在以下几个方面存在明显区别:
-
可变性:
- 列表是可变的,这意味着可以在列表创建后添加、删除或修改元素。
- 元组是不可变的,一旦创建,其元素就不能被修改(除非元素本身是可变类型,如列表,但这种修改不改变元组的结构)。
- 字典的键是不可变的,但值是可变的,可以添加、删除或修改键值对。
-
数据结构:
- 列表和元组是有序的序列,元素按照插入的顺序排列,并且可以通过索引访问。
- 字典是无序的键值对集合,通过键来快速查找对应的值,而不是通过索引。
-
使用场景:
-
当需要存储一组有序且可能会经常变动的数据时,列表是一个很好的选择,例如存储学生的成绩列表,可能会随时添加或修改成绩。
-
元组适用于存储一些不希望被修改的数据,例如表示一个点的坐标
(x, y),或者函数返回多个固定值时,使用元组可以保证数据的完整性和不可变性。 -
字典常用于存储具有映射关系的数据,例如学生的姓名和成绩的对应关系,通过姓名(键)可以快速找到对应的成绩(值),方便数据的查找和管理。
-
通过对Python知识架构的梳理以及对数据类型的深入学习和操作,我对Python的理解和应用能力得到了进一步提升,为后续更深入的学习和实际项目开发奠定了坚实的基础。
相关文章:

No. 34 笔记 | Python知识架构与数据类型相关内容 | 实操
在今天的Python学习中,我对Python的知识架构有了更深入的理解,同时也对Python的数据类型及其操作有了全面的认识和实践。 一、Python知识架构理解 Python是一门功能强大且应用广泛的编程语言,其知识架构可以从多个层面来理解。 从整体结构上…...

【2024年华为OD机试】 (B卷,100分)- 字符串分割(Java JS PythonC/C++)
一、问题描述 题目解析 问题描述 给定一个非空字符串 s,要求将该字符串分割成若干子串,使得每个子串的 ASCII 码值之和均为“水仙花数”。具体要求如下: 若分割不成功,则返回 0;若分割成功且分割结果不唯一,则返回 -1;若分割成功且分割结果唯一,则返回分割后子串的数…...

Pix2Pix :用于图像到图像转换的条件生成对抗网络
1. 背景与问题 图像到图像的转换(Image-to-Image Translation)是计算机视觉中的一个重要任务,指的是在输入一张图像的情况下,生成一张风格、内容或其他条件不同但语义一致的图像。随着深度学习的发展,尤其是生成对抗网…...

基于VSCODE+GDB+GDBSERVER远程单步调试设备篇(可视化界面)
目录 说明 配置方法 1)VSCODE必备插件 2)配置launch.json文件,用于GDB调试 调试步骤 目标板运行程序 1)已启动程序,通过attach方式进入调试 2)通过gdbserver启动时加载程序(程序路径根据实际情…...

CamemBERT:一款出色的法语语言模型
摘要 预训练语言模型在自然语言处理中已无处不在。尽管这些模型取得了成功,但大多数可用模型要么是在英语数据上训练的,要么是在多种语言数据拼接的基础上训练的。这使得这些模型在除英语以外的所有语言中的实际应用非常有限。本文探讨了为其他语言训练…...

0基础跟德姆(dom)一起学AI 自然语言处理18-解码器部分实现
1 解码器介绍 解码器部分: 由N个解码器层堆叠而成每个解码器层由三个子层连接结构组成第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接第二个子层连接结构包括一个多头注意力子层和规范化层以及一个残差连接第三个子层连接结构包括一个前馈全连接子层…...

我的创作纪念日——我与CSDN一起走过的365天
目录 一、机缘:旅程的开始 二、收获:沿路的花朵 三、日常:不断前行中 四、成就:一点小确幸 五、憧憬:梦中的重点 一、机缘:旅程的开始 最开始开始写博客是在今年一二月份的时候,也就是上一…...

C++:bfs解决多源最短路与拓扑排序问题习题
1. 多源最短路 其实就是将所有源头都加入队列, 01矩阵 LCR 107. 01 矩阵 - 力扣(LeetCode) 思路 求每个元素到离其最近0的距离如果我们将1当做源头加入队列的话,无法处理多个连续1的距离存储,我们反其道而行之&…...

【面试题】JVM部分[2025/1/13 ~ 2025/1/19]
JVM部分[2025/1/13 ~ 2025/1/19] 1. JVM 由哪些部分组成?2. Java 的类加载过程是怎样的?3. 请你介绍下 JVM 内存模型,分为哪些区域?各区域的作用是什么?4. JVM 垃圾回收调优的主要目标是什么?5. 如何对 Jav…...

文献综述相关ChatGPT提示词分享
文献综述 ChatGPT 可以帮助提高文献综述的有效性和全面性。ChatGPT可以高效搜索和审查与宝子们课题研究相关的文献资料来源。一些给力的插件工具还可以帮助您总结复杂的研究论文并提取信息以更快更好地消化信息。合理的运用ChatGPT和GPTs可以提高文献综述的清晰度和质量&#…...

Excel 技巧14 - 如何批量删除表格中的空行(★)
本文讲如何批量删除表格中的空行。 1,如何批量删除表格中的空行 要点就是按下F5,然后选择空值条件以定位所有空行,然后删除即可。 按下F5 点 定位条件 选 空值,点确认 这样就选中了空行 然后点右键,选 删除 选中 下方…...

图片生成Prompt编写技巧
1. 图片情绪(场景氛围) 一张图片一般都会有一个情绪基调,因为作画本质上也是在传达一些情绪,一般都会借助图片的氛围去转达。例如:比如家庭聚会一般是欢乐、喜乐融融。断壁残垣一般是悲凉。还有萧瑟、孤寂等。 2.补充细…...

【STM32-学习笔记-4-】PWM、输入捕获(PWMI)
文章目录 1、PWMPWM配置 2、输入捕获配置3、编码器 1、PWM PWM配置 配置时基单元配置输出比较单元配置输出PWM波的端口 #include "stm32f10x.h" // Device headervoid PWM_Init(void) { //**配置输出PWM波的端口**********************************…...
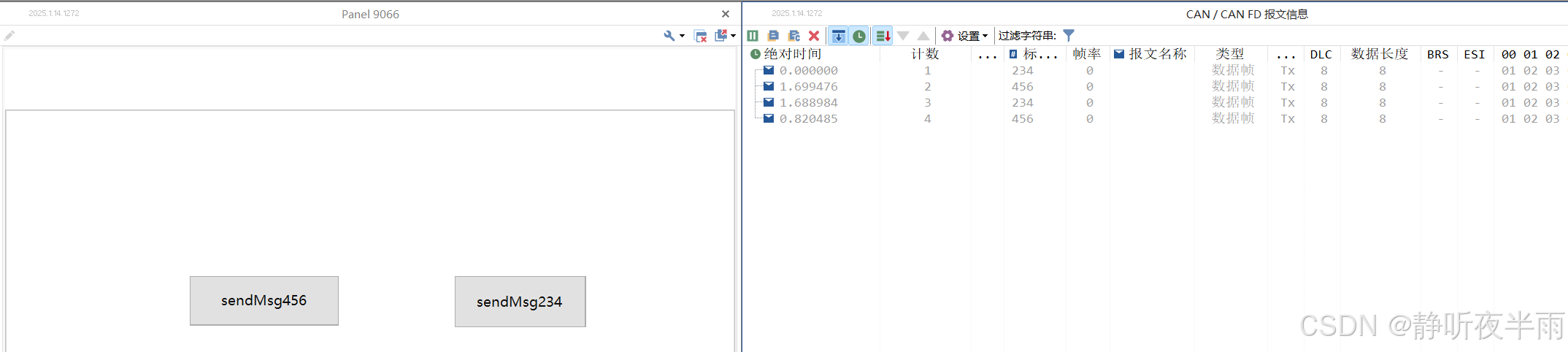
TOSUN同星TsMaster使用入门——3、使用系统变量及c小程序结合panel面板发送报文
本篇内容将介绍TsMaster中常用的Panel面板控件以及使用Panel控件通过系统变量以及c小程序来修改信号的值,控制报文的发送等。 目录 一、常用的Panel控件介绍 1.1系统——启动停止按钮 1.2 显示控件——文本框 1.3 显示控件——分组框 1.4 读写控件——按钮 1.…...

【Web】2025-SUCTF个人wp
目录 SU_blog SU_photogallery SU_POP SU_blog 先是注册功能覆盖admin账号 以admin身份登录,拿到读文件的权限 ./article?filearticles/..././..././..././..././..././..././etc/passwd ./article?filearticles/..././..././..././..././..././..././proc/1…...

React进阶之react.js、jsx模板语法及babel编译
React React介绍React官网初识React学习MVCMVVM JSX外部的元素props和内部的状态statepropsstate 生命周期constructorgetDerivedStateFromPropsrendercomponentDidMount()shouldComponentUpdategetSnapshotBeforeUpdate(prevProps, prevState) 创建项目CRA:create-…...

在Linux上如何让ollama在GPU上运行模型
之前一直在 Mac 上使用 ollama 所以没注意,最近在 Ubuntu 上运行发现一直在 CPU 上跑。我一开始以为是超显存了,因为 Mac 上如果超内存的话,那么就只用 CPU,但是我发现 Llama3.2 3B 只占用 3GB,这远没有超。看了一下命…...

R 语言科研绘图第 20 期 --- 箱线图-配对
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

suctf2025
Suctf2025 --2标识为看的wp,没环境复现了 所有参考资料将在文本末尾标明 WEB SU_photogallery 思路👇 构造一个压缩包,解压出我们想解压的部分,然后其他部分是损坏的,这样是不是就可以让整个解压过程是出错的从而…...

Quinlan C4.5剪枝U(0,6)U(1,16)等置信上限如何计算?
之前看到Quinlan中关于C4.5决策树算法剪枝环节中,关于错误率e置信区间估计,为啥 当E=0时,U(0,1)=0.75,U(0,6)=0.206,U(0,9)=0.143? 而当E不为0时,比如U(1,16)=0.157,如图: 关于C4.5决策树,Quinlan写了一本书,如下: J. Ross Quinlan (Auth.) - C4.5. Programs f…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
