Day 17 卡玛笔记
这是基于代码随想录的每日打卡

654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:

输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:

输入:nums = [3,2,1]
输出:[3,null,2,null,1]
递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:# 递归终止条件if len(nums)==1:return TreeNode(nums[0])# 递归逻辑# 找最大值max_val=max(nums)root=TreeNode(max_val)# 最大值索引index=nums.index(max_val)# 左数组left_nums=nums[:index]# 右数组right_nums=nums[index+1:]# 如果左数组个数大于1才能递归if len(left_nums)>=1:left_child=self.constructMaximumBinaryTree(left_nums)root.left=left_child# 如果左数组没有元素则指向空,其实本来就默认指向空,这里为了逻辑完整好理解else:root.left=None# 右数组同上if len(right_nums)>=1:right_child=self.constructMaximumBinaryTree(right_nums)root.right=right_childelse:root.right=Nonereturn root
运行结果

617. 合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:

输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:# 递归终止条件if root1==None and root2!=None:return root2if root1!=None and root2==None:return root1if root1==None and root2==None:return None# 递归逻辑# 这里开辟一个新二叉树,不过也可以直接在tree1或者tree2上直接进行修改root_val=root1.val+root2.valroot=TreeNode(root_val)root.left=self.mergeTrees(root1.left,root2.left)root.right=self.mergeTrees(root1.right,root2.right)return root

700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:

输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例 2:

输入:root = [4,2,7,1,3], val = 5
输出:[]
递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if root==val:return root# 递归终止条件if root==None:return Noneif root.val==val:return root# 递归逻辑 if root.val>val:return self.searchBST(root.left,val)if root.val<val:return self.searchBST(root.right,val)
运行结果

迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:while root:if root.val>val:root=root.leftelif root.val<val:root=root.rightelse:# 相等情况return root# 没找到,返回Nonereturn None
运行结果

98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def __init__(self):self.pre=Nonedef isValidBST(self, root: Optional[TreeNode]) -> bool:# 由于二叉搜索树按中序遍历就是单调递增,所以递归按照中序遍历来# 递归终止条件if root==None:return True# 递归逻辑left=self.isValidBST(root.left)if self.pre and self.pre.val>=root.val:return Falseelse:self.pre=rootright=self.isValidBST(root.right)return left and right
运行结果
有问题欢迎评论或私信
相关文章:

Day 17 卡玛笔记
这是基于代码随想录的每日打卡 654. 最大二叉树 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建: 创建一个根节点,其值为 nums 中的最大值。递归地在最大值 左边 的 子数组前缀上 构建左子树。递归地在最大值 右边 的 子数组…...
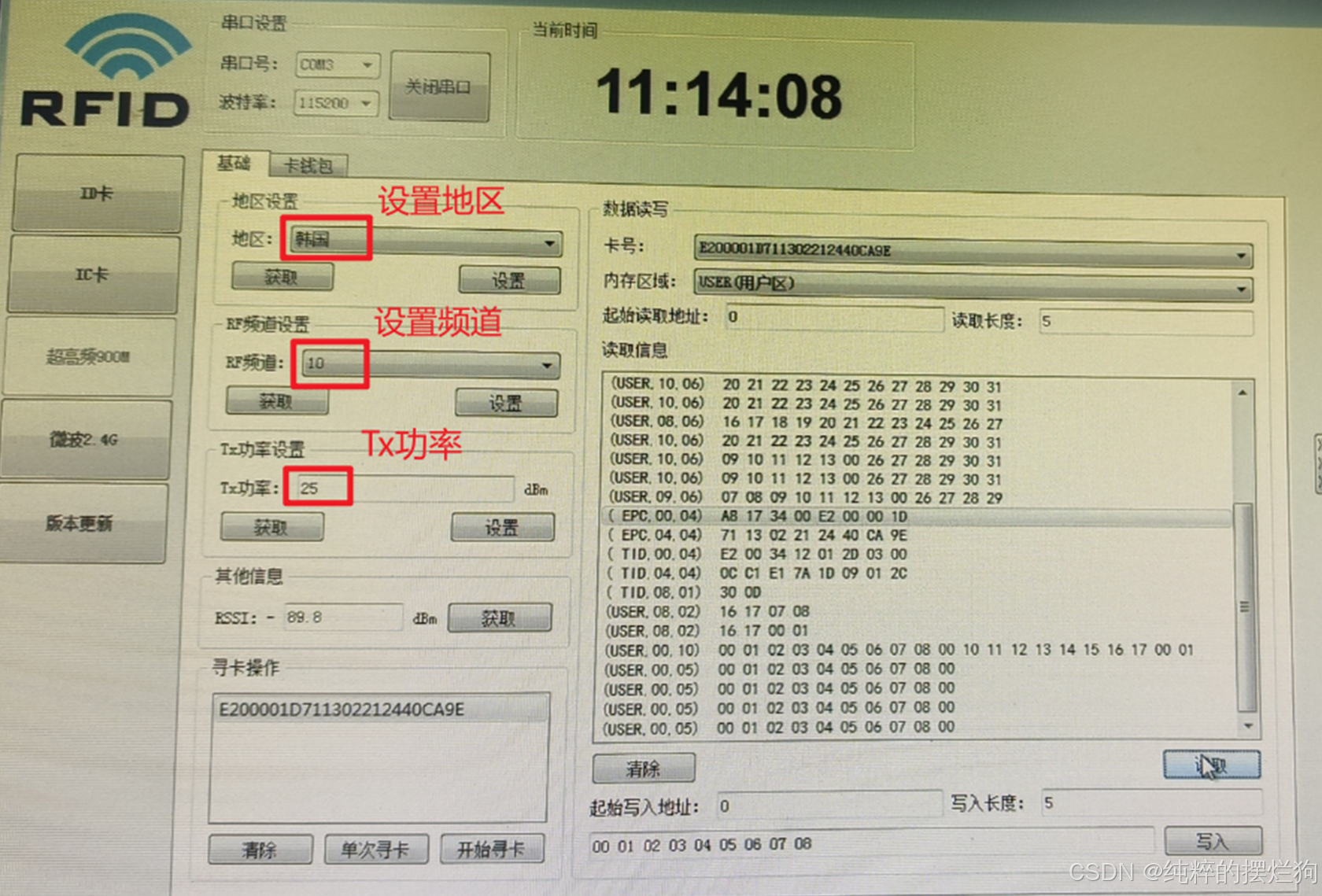
深圳大学-智能网络与计算-实验一:RFID原理与读写操作
实验目的与要求 掌握超高频RFID标签的寻卡操作。掌握超高频RFID标签的读写操作。掌握超高频RFID标签多张卡读取时的防冲突机制。 方法,步骤 软硬件的连接与设置超高频RFID寻卡操作超高频RFID防冲突机制超高频RFID读写卡操作 实验过程及内容 一.软硬…...

⚡C++ 中 std::transform 函数深度解析:解锁容器元素转换的奥秘⚡【AI 润色】
在 C 编程的世界里,我们常常需要对容器中的元素进行各种转换操作。无论是将数据进行格式调整,还是对元素进行数学运算,高效的转换方法都是提升代码质量和效率的关键。std::transform函数作为 C 标准库<algorithm &g…...
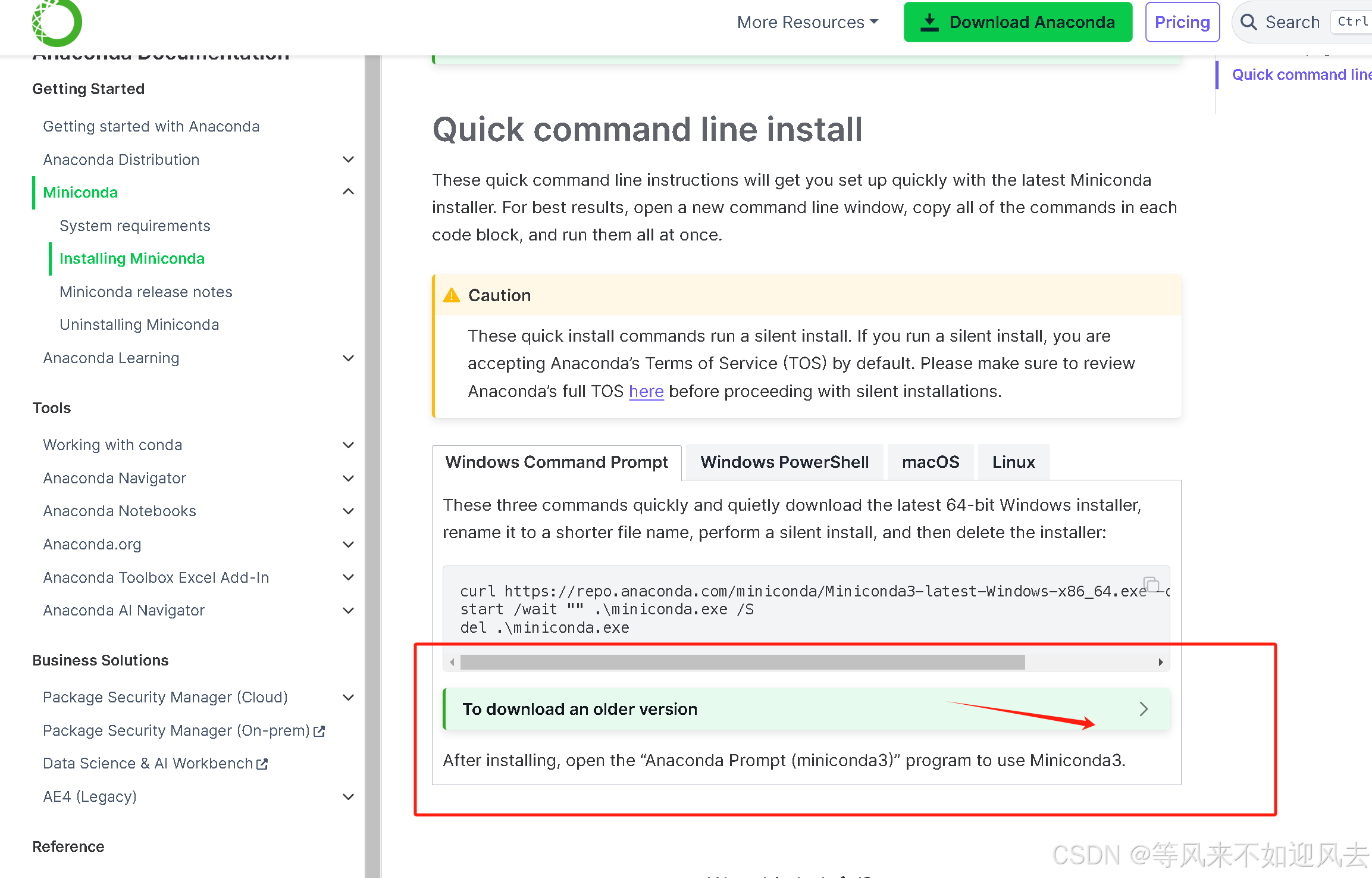
【miniconda】:langraph的windows构建
langraph需要python3.11 langraph强烈建议使用py3.11 默认是3.12 官方 下载仓库 下载老版本的python (后续发现新版miniconda也能安装老版本的python) 在这里...
(k8s)k8s部署mysql与redis(无坑版)
0.准备工作 在开始之前,要确保我们的节点已经加入网络并且已经准备好,如果没有可以去看我前面发表的踩坑与解决的文章,希望能够帮到你。 1.k8s部署redis 1.1目标 由于我们的服务器资源较小,所以决定只部署一个redis副本&#x…...

Git常用操作指令
初始化配置 # 配置全局用户名和邮箱 git config --global user.name "账号" git config --global user.email "邮箱"# 查看配置信息 git config --list仓库初始化创建新的 Git 仓库: # 初始化新仓库 git init# 克隆远程仓库 git clone URL状态…...

新手理解:Android 中 Handler 和 Thread.sleep 的区别及应用场景
新手理解:Android 中 Handler 和 Thread.sleep 的区别及应用场景 Handler 是啥?Handler 的几个核心功能: Thread.sleep 是啥?Thread.sleep 的核心特点: 两者的区别它们的应用场景1. Handler 的应用场景2. Thread.sleep…...

智能安全策略-DPL
一、华三防火墙-接口的概念。 1、接口。 1. 什么是接口? 接口就像是防火墙的“门”,用来连接不同的网络设备,比如电脑、路由器、服务器等。通过这些“门”,数据(比如网页、视频、文件)才能进出防火墙。 …...
 算法详解及案例分析)
差分进化算法 (Differential Evolution) 算法详解及案例分析
差分进化算法 (Differential Evolution) 算法详解及案例分析 目录 差分进化算法 (Differential Evolution) 算法详解及案例分析1. 引言2. 差分进化算法 (DE) 算法原理2.1 基本概念2.2 算法步骤3. 差分进化算法的优势与局限性3.1 优势3.2 局限性4. 案例分析4.1 案例1: 单目标优化…...

Alibaba Spring Cloud 十七 Sentinel熔断降级
概述 在微服务架构中,熔断与降级是保证系统稳定性的重要机制,能有效防止故障蔓延或雪崩效应。当某个服务出现异常、延迟过高或错误率过高时,触发熔断保护,将该服务“隔离”一段时间,避免影响整体系统的吞吐和可用性。 …...

LetsWave脑电数据简单ERP分析matlab(一)
LetsWave是基于matlab的一款工具包,类似eeglab,也可以对数据进行预处理。习惯使用eeglab做数据预处理的,可以先在eeglab中做预处理,然后可以保存为*.set格式,最后在letswave中画图。 letswave下载地址:htt…...

设计模式Python版 工厂方法模式
文章目录 前言一、工厂方法模式二、工厂方法模式示例三、工厂方法模式客户端改进四、工厂方法模式隐藏工厂方法(可选) 前言 GOF设计模式分三大类: 创建型模式:关注对象的创建过程,包括单例模式、简单工厂模式、工厂方…...

贝叶斯优化相关
贝叶斯优化相关 python中有很多模块支持贝叶斯优化,如bayesian-optimization、hyperopt,比较好用的是hyperopt,下面是对hyperopt文章的翻译,原文地址如下 https://districtdatalabs.silvrback.com/parameter-tuning-with-hyperop…...

【Matlab高端绘图SCI绘图全家桶更新版】在原60种绘图类型基础上更新
俗话说,一图胜千言。数据可视化便是将数据通过图形化的方式展现出来,它更加便于我们观察数据蕴含的的规律,洞察了数据蕴含的规律后,从而使我们能够做更好的进行科研表达和学术写作。 科研过程中,绘图是一项非常重要的…...

如何构建一个 GraphRAG 系统
构建一个 GraphRAG 系统以提升传统 RAG(检索增强生成)模型的性能,需要结合知识图谱和生成式语言模型的能力,以下是实现的关键步骤和方法: 1. 数据准备 (1) 收集数据 确保有足够的高质量文本数据源,如&…...

代码随想录算法训练营day34
代码随想录算法训练营 —day34 文章目录 代码随想录算法训练营前言一、62.不同路径动态规划动态规划空间优化 二、63. 不同路径 II动态规划动态规划优化空间版 三、343. 整数拆分动态规划贪心算法 96.不同的二叉搜索树总结 前言 今天是算法营的第34天,希望自己能够…...

单片机基础模块学习——按键
一、按键原理图 当把跳线帽J5放在右侧,属于独立按键模式(BTN模式),放在左侧为矩阵键盘模式(KBD模式) 整体结构是一端接地,一端接控制引脚 之前提到的都是使用了GPIO-准双向口的输出功能&#x…...

polars as pl
import polars as pl#和pandas类似,但是处理大型数据集有更好的性能. #necessary import pandas as pd#导入csv文件的库 import numpy as np#进行矩阵运算的库 #metric from sklearn.metrics import roc_auc_score#导入roc_auc曲线 #KFold是直接分成k折,StratifiedKFold还要考虑…...
)
重构(4)
(一)添加解释性变量,使得代码更容易理解,更容易调试,也可以方便功能复用 解释性的变量 总价格为商品总价(单价*数量)-折扣(超过100个以上的打9折)邮费(原价的…...
神经网络|(三)线性回归基础知识
【1】引言 前序学习进程中,已经对简单神经元的工作模式有所了解,这种二元分类的工作机制,进一步使用sigmoid()函数进行了平滑表达。相关学习链接为: 神经网络|(一)加权平均法,感知机和神经元-CSDN博客 神经网络|(二…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
