代码随想录算法训练营day34
代码随想录算法训练营
—day34
文章目录
- 代码随想录算法训练营
- 前言
- 一、62.不同路径
- 动态规划
- 动态规划空间优化
- 二、63. 不同路径 II
- 动态规划
- 动态规划优化空间版
- 三、343. 整数拆分
- 动态规划
- 贪心算法
- 96.不同的二叉搜索树
- 总结
前言
今天是算法营的第34天,希望自己能够坚持下来!
今日任务:
● 62.不同路径
● 63. 不同路径 II
● 343. 整数拆分(思路较难)
● 96. 不同的二叉搜索树(思路较难)
一、62.不同路径
题目链接
文章讲解
视频讲解
动态规划
思路:
- dp[i][j]的定义为:走到[i,j]位置有多少种路径
- 递归公式:对于dp[i][j]都是由上一个位置或者左边的位置移动得来,所有有
dp[i][j] = dp[i-1][j] + dp[i][j-1] - 初始化:因为递推公式需要上面的位置和左边的位置来推导,所以初始化第一行和左边第一列,且走到这些位置都只有一种路径,dp[i][0] = 1, dp[0][i] = 1
- 遍历顺序:因为递推公式是从前往后的,所以遍历顺序是从前往后
代码如下:
class Solution {
public://dp[i][j]含义:走到[i,j]位置有多少种路径//递推公式:dp[i][j] = dp[i-1][j] + dp[i][j-1]//初始化: dp[i][0] = 1, dp[0][i] = 1//遍历顺序:左->右, 上->下int uniquePaths(int m, int n) {//int dp[m][n];vector<vector<int>>dp (m, vector<int>(n,0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int i = 0; i < n; i++) dp[0][i] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m-1][n-1];}
};
动态规划空间优化
因为实际上只跟上层对应的格子有关,左边的是由上一次递推而来,所以只需要维护一层的数组,递推公式上就是把dp[i]维度去掉。
代码如下:
class Solution {
public://dp[i][j]含义:走到[i,j]位置有多少种路径//递推公式:dp[i][j] = dp[i-1][j] + dp[i][j-1]//初始化: dp[i][0] = 1, dp[0][i] = 1//遍历顺序:左->右, 上->下int uniquePaths(int m, int n) {vector<int>dp (n,1); //因为直接上只跟上层对应的格子有关,左边的已知了,所以只需要维护一层的数组for (int i = 1; i < m; i++) { //i+1:下一层for (int j = 1; j < n; j++) { //本层从左到右遍历dp[j] = dp[j] + dp[j - 1]; //本层的第j个格子=上层对应的格子+本层左边的格子}}return dp[n-1];}
};
二、63. 不同路径 II
题目链接
文章讲解
视频讲解
思路:
跟62.不同路径的区别就是多了个障碍,如果是障碍的话,就标记相应的dp[i]=0就可以了。
- dp[i][j]的定义为:表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 递归公式:因为需要考虑障碍,当(i, j)没有障碍的时候,再推导dp[i][j]
if (obstacleGrid[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; - 初始化:dp[i][0]和dp[0][j]还是一样是1,但是如果有障碍的话,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
- 遍历顺序:因为递推公式是从前往后的,所以遍历顺序是从前往后,从上到下

拿示例1来举例如题:
对应的dp table 如图:

动态规划
代码如下:
class Solution {
public://dp[i][j]含义:走到[i,j]位置有多少种路径//递推公式:if(obs[i][j]!= 0) dp[i][j] = dp[i-1][j] + dp[i][j-1] //初始化: dp[i][0] = 1, dp[0][i] = 1, 当遍历碰到障碍物时,后面的都是0//遍历顺序:左->右, 上->下int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();//如果在起点或终点就有障碍if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;vector<vector<int>>dp (m, vector<int>(n,0));//初始化,遇到障碍后终止for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[0][i] = 1;for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue; //有障碍则跳过dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
};
动态规划优化空间版
同样的,因为实际上只跟上层对应的格子有关,左边的是由上一次递推而来,所以只需要维护一层的数组,递推公式上就是把dp[i]维度去掉。
代码如下:
class Solution {
public://dp[i][j]含义:走到[i,j]位置有多少种路径//递推公式:if(obs[i][j]!= 0) dp[i][j] = dp[i-1][j] + dp[i][j-1] //初始化: dp[i][0] = 1, dp[0][i] = 1, 当遍历碰到障碍物时,后面的都是0//遍历顺序:左->右, 上->下int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();//如果在起点或终点就有障碍if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1) return 0;vector<int> dp(n,0);for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) dp[i] = 1;for (int i = 1; i < m; i++) {for (int j = 0; j < n; j++) { //这里要从0开始,因为前面只对obstacleGrid[0][i]进行了判断//每下一行i+1,都需要判断当前dp[0]是有障碍 if (obstacleGrid[i][j] == 1) dp[j] = 0; //这里不能用continue,不管是否有障碍,都需要更新dp[j]else if (j != 0)dp[j] = dp[j] + dp[j-1];}}return dp[n-1];}
};
三、343. 整数拆分
题目链接
文章讲解
视频讲解
动态规划
思路:
- dp[i]的定义为: 对于整数i,拆分后的最大乘积
- 递归公式:dp[i] 可能来自于两种情况:
①直接分出来的一个j, j与剩余的数相乘:j * (i - j)
②分出来j后,对剩余的数也拆分:j * dp[i-j], dp[i-j]就是对i-j进行拆分后得到最大乘积 - 初始化:dp[0] = 0, dp[1] = 0, dp[2] = 1,那么遍历的时候就可以从3开始
- 遍历顺序:遍历[3,n],每一个数再通过遍历[1,i](枚举从i中拆分出来的j)求出dp[i]
- 举例推导dp数组:
举例当n为10 的时候,dp数组里的数值,如下:

代码如下:
class Solution {
public://d[i]:对于整数i,拆分后的最大乘积//递推公式:dp[i] 可能来自于两种情况:// 1、直接分出来的一个j, j与剩余的数相乘:j * (i - j) // 2、分出来j后,最剩余的数也拆分:j * dp[i-j], dp[i-j]就是对i-j进行拆分后得到最大乘积//初始化:dp[0] = 0, dp[1] = 0, dp[2] = 1//遍历顺序:遍历[3,n],每一个数再通过遍历[1,i]求出dp[i]int integerBreak(int n) {vector<int> dp(n + 1, 0); //因为要求的是d[n],创建一个n+1大小的数组dp[2] = 1;for (int i = 3; i <= n; i++) {//注意 枚举j的时候,是从1开始的。从0开始的话,那么让拆分一个数拆个0,求最大乘积就没有意义了。for (int j = 1; j <= i/2; j++) { //这里直到i/2就结束了,因为最大乘积不会在i/2之后出现dp[i] = max(max((i - j) * j, j * dp[i-j]), dp[i]);}}return dp[n];}
};
贪心算法
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
代码如下:
class Solution {
public:int integerBreak(int n) {if (n == 2) return 1;if (n == 3) return 2;if (n == 4) return 4;int result = 1;while (n > 4) {result *= 3;n -= 3;}result *= n;return result;}
};
96.不同的二叉搜索树
题目链接
文章讲解
视频讲解
思路:
- dp[i]的定义为:i个节点有多少种二叉搜索树
- 递归公式:dp[i]等于遍历[1,i],计算分别以j为节点的种数累加
以j为节点的种数又等于以j为节点后,左子树的种数*右子树的种数= dp[j-1]*dp[i-j] - 初始化:0个节点是1种,dp[0] = 1, 其他节点都可以通过dp[0]推出
- 遍历顺序:因为递推公式是从前往后的,所以遍历顺序是从前往后
代码如下:
class Solution {
public://dp[i]:i个节点有多少种二叉搜索树//递推公式:dp[i]等于遍历[1,i],计算分别以j为节点的种数累加//以j为节点的种数又等于以j为节点后,左子树的种数*右子树的种数= dp[j-1]*dp[i-j]//初始化:0个节点是1种,dp[0] = 1, 其他节点都可以通过dp[0]推出int numTrees(int n) {vector<int> dp(n + 1, 0);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j]; }}return dp[n];}
};
总结
动态规划的dp数组,通常二维的可以优化空间去掉dp[i]维度,但是不太好理解,遍历的时候也需要一些细节上的改动。
明天继续加油!
相关文章:

代码随想录算法训练营day34
代码随想录算法训练营 —day34 文章目录 代码随想录算法训练营前言一、62.不同路径动态规划动态规划空间优化 二、63. 不同路径 II动态规划动态规划优化空间版 三、343. 整数拆分动态规划贪心算法 96.不同的二叉搜索树总结 前言 今天是算法营的第34天,希望自己能够…...

单片机基础模块学习——按键
一、按键原理图 当把跳线帽J5放在右侧,属于独立按键模式(BTN模式),放在左侧为矩阵键盘模式(KBD模式) 整体结构是一端接地,一端接控制引脚 之前提到的都是使用了GPIO-准双向口的输出功能&#x…...

polars as pl
import polars as pl#和pandas类似,但是处理大型数据集有更好的性能. #necessary import pandas as pd#导入csv文件的库 import numpy as np#进行矩阵运算的库 #metric from sklearn.metrics import roc_auc_score#导入roc_auc曲线 #KFold是直接分成k折,StratifiedKFold还要考虑…...
)
重构(4)
(一)添加解释性变量,使得代码更容易理解,更容易调试,也可以方便功能复用 解释性的变量 总价格为商品总价(单价*数量)-折扣(超过100个以上的打9折)邮费(原价的…...
神经网络|(三)线性回归基础知识
【1】引言 前序学习进程中,已经对简单神经元的工作模式有所了解,这种二元分类的工作机制,进一步使用sigmoid()函数进行了平滑表达。相关学习链接为: 神经网络|(一)加权平均法,感知机和神经元-CSDN博客 神经网络|(二…...

deepseek R1 高效使用学习
直接提问 1、可以看到思考过程,可以当个学习工具 2、高效简介代码prompt <context> You are an expert programming AI assistant who prioritizes minimalist, efficient code. You plan before coding, write idiomatic solutions, seek clarification …...

STM32_SD卡的SDIO通信_基础读写
本篇将使用CubeMXKeil, 创建一个SD卡读写的工程。 目录 一、SD卡要点速读 二、SDIO要点速读 三、SD卡座接线原理图 四、CubeMX新建工程 五、CubeMX 生成 SD卡的SDIO通信部分 六、Keil 编辑工程代码 七、实验效果 实现效果,如下图: 一、SD卡 速读…...

【Docker】私有Docker仓库的搭建
一、准备工作 确保您的系统已安装Docker。如果没有安装,请参考Docker官方文档进行安装。 准备一个用于存储仓库数据的目录,例如/registry_data/。 二、拉取官方registry镜像 首先,我们需要从Docker Hub拉取官方的registry镜像。执行以下命…...

linux 管道符、重定向与环境变量
1. 输入输出重定向 在linux工作必须掌握的命令一文中,我们已经掌握了几乎所有基础常用的Linux命令,那么接下来的任务就是把多个命令适当的组合到一起,使其协同工作,会更高效的处理数据,做到这一点就必须搞清楚命令的输…...

Ansible fetch模块详解:轻松从远程主机抓取文件
在自动化运维的过程中,我们经常需要从远程主机下载文件到本地,以便进行分析或备份。Ansible的fetch模块正是为了满足这一需求而设计的,它可以帮助我们轻松地从远程主机获取文件,并将其保存到本地指定的位置。在这篇文章中…...
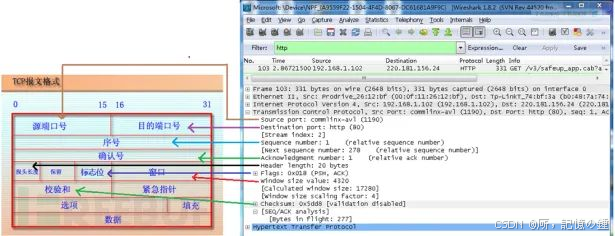
wireshark工具简介
目录 1 wireshark介绍 2 wireshark抓包流程 2.1 选择网卡 2.2 停止抓包 2.3 保存数据 3 wireshark过滤器设置 3.1 显示过滤器的设置 3.2 抓包过滤器 4 wireshark的封包列表与封包详情 4.1 封包列表 4.2 封包详情 参考文献 1 wireshark介绍 wireshark是非常流行的网络…...

51单片机——按键控制LED流水灯
引言 在电子制作和嵌入式系统学习中,51 单片机是一个经典且入门级的选择。按键控制 LED 流水灯是 51 单片机的一个基础应用,通过这个实例,我们可以深入了解单片机的输入输出控制原理。 51 单片机简介 51 单片机是对所有兼容 Intel 8051 指…...

【opencv】第9章 直方图与匹配
第9章 直方图与匹配 9.1 图像直方图概述 直方图广泛运用于很多计算机视觉运用当中,通过标记帧与帧之间显著的边 缘和颜色的统计变化,来检测视频中场景的变化。在每个兴趣点设置一个有相近 特征的直方图所构成“标签”,用以确定图像中的兴趣点。边缘、色…...

HTML5 Web Worker 的使用与实践
引言 在现代 Web 开发中,用户体验是至关重要的。如果页面在执行复杂计算或处理大量数据时变得卡顿或无响应,用户很可能会流失。HTML5 引入了 Web Worker,它允许我们在后台运行 JavaScript 代码,从而避免阻塞主线程,保…...

MVCC底层原理实现
MVCC的实现原理 了解实现原理之前,先理解下面几个组件的内容 1、 当前读和快照读 先普及一下什么是当前读和快照读。 当前读:读取数据的最新版本,并对数据进行加锁。 例如:insert、update、delete、select for update、 sele…...

基于ESP32-IDF驱动GPIO输出控制LED
基于ESP32-IDF驱动GPIO输出控制LED 文章目录 基于ESP32-IDF驱动GPIO输出控制LED一、点亮LED3.1 LED电路3.2 配置GPIO函数gpio_config()原型和头文件3.3 设置GPIO引脚电平状态函数gpio_set_level()原型和头文件3.4 代码实现并编译烧录 一、点亮LED 3.1 LED电路 可以看到&#x…...

【优选算法】9----长度最小的子数组
----------------------------------------begin-------------------------------------- 铁子们,前面的双指针算法篇就算告一段落啦~ 接下来是我们的滑动窗口篇,不过有一说一,算法题就跟数学题一样,只要掌握方法,多做…...

LabVIEW太阳能照明监控系统
在公共照明领域,传统的电力照明系统存在高能耗和维护不便等问题。利用LabVIEW开发太阳能照明监控系统,通过智能控制和实时监测,提高能源利用效率,降低维护成本,实现照明系统的可持续发展。 项目背景 随着能源危机…...

MongoDB中单对象大小超16M的存储方案
在 MongoDB 中,单个文档的大小限制为 16MB。如果某个对象(文档)的大小超过 16MB,可以通过以下几种方案解决: 1. 使用 GridFS 适用场景:需要存储大文件(如图像、视频、文档等)。 原…...

三维激光扫描-用智能检测系统提升效率
当下,企业对生产效率和质量控制的要求越来越高。传统的检测方法往往难以满足高精度、快速响应的需求。三维激光扫描技术结合智能检测系统,为工业检测带来了革命性的变革。 传统检测方法的局限性 传统检测方法主要依赖于人工测量和机械检测工具…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
