刷题总结 回溯算法
为了方便复习并且在把算法忘掉的时候能尽量快速的捡起来
刷完回溯算法这里需要做个总结
回溯算法的适用范围
回溯算法是深度优先搜索(DFS)的一种特定应用,在DFS的基础上引入了约束检查和回退机制。
相比于普通的DFS,回溯法的优势主要体现在解决需要约束条件判断、剪枝和回退的复杂问题上。
实际应用时有易于识别的题目类型特征:组合、分割、子集、排列、棋盘等
这些问题的共同点是解空间均为层次结构,因此回溯算法就是对回溯树进行DFS
模式识别
根据自己刷题的感受,并统计做题过程中思路上遇到过的槛,
归纳后可以得到以下模式识别树,
专门用于看到题目后进行模式识别,
快速找到解题方法:

该模式识别树综合搜索集类型、搜索规则和结果收集条件等因素
接下来对当前的模式识别树进行简单解释:
回溯算法总模板:
def backtracking(self, 参数):if 终止条件存放结果returnfor 选择:本层集合中元素(树中节点孩子的数量就是集合的大小):处理节点self.backtracking(路径,选择列表) // 递归回溯,撤销处理结果步骤:1.函数(无返回值,参数多) + 2.if(终止){收集+return} + 3.for(搜索集){处理;递归;回溯}
回溯树:

一、题目类型
回溯算法常用于解决问题:组合、分割、子集、排列、棋盘等
在我眼里以上题目类型可以总结为三个大类:组合类问题、排列类问题和约束满足类问题,
因此,这几个大类是根据解空间(回溯树)的层次结构进行划分的,
而且对模板的应用有较大的影响

1.组合类问题:层内层间顺序访问
包含类型:组合、分割、子集
模板变体:
def backtracking(self, 输入参数, start_idx, path, ans):if 终止条件存放结果returnfor i in range(start_idx, len(总搜索集)):if 约束条件:continue # 有时需要break处理节点self.backtracking(输入参数, start_idx + 1, path, ans) // 递归回溯,撤销处理结果或
def backtracking(self, 输入参数, start_idx, path, ans):if 终止条件存放结果returnfor i in range(start_idx, len(总搜索集)):if 约束条件:处理节点self.backtracking(输入参数, start_idx + 1, path, ans) // 递归回溯,撤销处理结果模式识别特征:
-
不考虑顺序
-
一般搜索集长度大于结果长度
-
回溯树层内层间顺序访问
题目列表:
组合
77. 组合
216. 组合总和 III
39. 组合总和
40. 组合总和 II
分割
131. 分割回文串
93. 复原 IP 地址
子集
78. 子集
90. 子集 II
491. 非递减子序列
这其中有一个特例就是重复选取题:39. 组合总和
递归命令需要改为:
# self.backtracking(输入参数, start_idx + 1, path, ans) // 递归
self.backtracking(输入参数, start_idx, path, ans) // 递归2.排列类问题:层内遍历访问层间顺序访问
包含类型:排列
模板变体:
该类型题目有visited数组写法、集合写法和交换元素三种写法,
visited数组普适性较强,以visited数组写法为例:
def backtracking(self, 输入参数, visited, path, ans):if 终止条件存放结果returnfor i in range(len(总搜索集)):if visited[i] or 其他约束条件:continue处理节点visited[i] = Trueself.backtracking(输入参数, visited, path, ans) // 递归visited[i] = False其他回溯,撤销处理结果模式识别特征:
-
考虑顺序
-
搜索集长度等于结果长度
-
回溯树层内遍历,层间顺序访问
题目列表:
46. 全排列
47. 全排列 II
3.约束满足问题:约束条件较强,无特定访问顺序
包含类型:安排行程、棋盘
相比于总模板无特定要求,但常需要主函数预处理搜索集以剪枝回溯树,实现高效搜索
模式识别特征:
-
一般类似于排列问题
-
有较强的约束条件
-
一般需要对搜索集预处理,否则会超时或代码过于复杂
题目列表:
332. 重新安排行程
棋盘
51. N 皇后
37. 解数独
二、几个需要注意的题目类型的约束条件
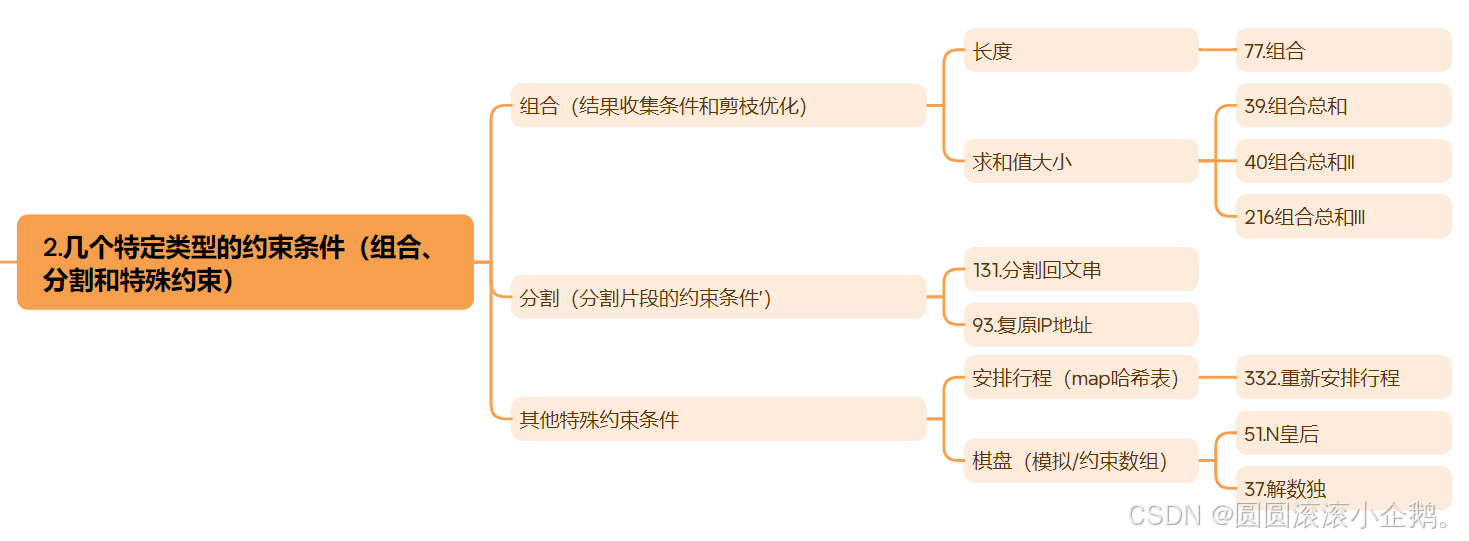
这个只有一个维度,目前共遇到三个种类:
1.组合:结果收集条件和剪枝优化
1.1 长度
用长度作为结果收集条件会产生两个结果:
(1)路径长度符合条件时收集结果并返回
(2)剪枝优化:搜索集末尾剪枝
可以通过控制单个节点内下一步访问的搜索集的末尾位置
实现方式未
把回溯树的末端指针从n调整到n - (k - len(path)) + 1
题目:
77. 组合
理解起来就是把末尾的(k - len(path))个路径去掉,
以长度作为结果收集条件的题目总搜索集长度 > 路径长度 + 节点内搜索集宽度
节点内搜索集宽度太大了,路径长度就达不到要求,
所以需要把回溯树的宽度从n调整到n - (k - len(path)) + 1,
末尾的+1是本轮访问的节点
1.2 求和值大小
类似于长度,也是有两个影响:
(1)路径求和等于目标数时收集结果并返回,大于目标数直接返回
(2)剪枝优化:排序break剪枝,
将搜索集排序,求和大于目标数舍弃节点所有后续路径
题目:
216. 组合总和 III
39. 组合总和
40. 组合总和 II
实现方式为:
如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历
注意主函数种要对总搜索集排序
2.分割:分割片段的约束条件
分割类题目对分割片段有特殊的要求,因此常采用以下模板范式:
def is_valid(self, 参数):判断条件def backtracking(self, 输入参数, start_idx, path, ans):if 终止条件存放结果returnfor i in range(start_idx, len(总搜索集)):if self.is_valid(参数):处理节点self.backtracking(输入参数, start_idx + 1, path, ans) // 递归回溯,撤销处理结果题目:
131. 分割回文串
93. 复原 IP 地址
3.其他特殊约束条件:棋盘、安排行程等
该类题,常常需要复杂的判断条件或在主函数中对搜索集预处理(常用哈希表)来辅助判断约束条件
其中复杂的判断条件可能导致超时,
在主函数中对搜索集预处理(常用哈希表)来辅助判断比较常用
题目:(预处理方式)
安排行程:map哈希表:
332. 重新安排行程
棋盘:数组哈希表:
51. N 皇后
37. 解数独
三、去重
1.组合问题中的去重
如果搜索集存在重复元素,则需要进行同层重复剪枝操作来去重,
否则由于回溯树中同一层存在重复元素,使得多条路径通向同一个结果
导致重复的组合结果,
去重方法可以分为索引去重和数值去重,但都需要排序,
其中排序有两个作用:使相同数字紧贴和防止异层重复访问
防止异层重复访问是去重能够在层内进行的前提,
索引去重便是利用相同数字紧贴的特性去重,有简单写法和数组写法两种写法
数值去重则是在层内统计同一个数值的使用情况来去重,不需要排序的第一个功能,
更详细介绍在刷题记录 回溯算法-13:90. 子集 II-CSDN博客
题目:
40. 组合总和 II
90. 子集 II
491. 非递减子序列
其中491. 非递减子序列情况特殊,只能用数值去重,详见刷题记录 回溯算法-14:491. 非递减子序列-CSDN博客
2.排列问题中的去重
和组合问题略有不同,排列问题除了层内去重还可以倒序去重,
层内去重逻辑和组合去重类似,索引去重和数值去重都可以用,同样需要排序,
但索引去重的简单写法无法使用,只能用数组写法
倒序去重很少用,以上详见:
刷题记录 回溯算法-16:47. 全排列 II-CSDN博客
题目:47. 全排列 II
四、遍历与搜索(递归函数返回)
大部分题目需要找到所有结果,但有些题目找到一个结果即可返回,其代码结构会出现一些变化
1.收集所有结果
大部分题目都需要用一个数组收集所有符合条件的结果,
这也是总模板适配的情况
def backtracking(self, 参数):if 终止条件存放结果returnfor 选择:本层集合中元素(树中节点孩子的数量就是集合的大小):处理节点self.backtracking(路径,选择列表) // 递归回溯,撤销处理结果2.找到一个结果
有些题目只需要找到一个结果即可,且往往尝试找到所有结果会导致超时,
这种情况需要用返回值在找到结果后快速返回主函数:
def backtracking(self, 参数):if 终止条件存放结果return Truefor 选择:本层集合中元素(树中节点孩子的数量就是集合的大小):处理节点if self.backtracking(路径,选择列表): # 递归return True回溯,撤销处理结果return False修改分为三处:
1.终止条件返回True
2.递归调用返回True
3.函数末尾返回False
题目:
332. 重新安排行程
37. 解数独
建议的复习方法
回溯算法类型的题目有较为统一的模板和容易识别的题目类型,
但各个类型都会有格子需要注意的点,
因此建议先简单过一遍模式识别树,熟悉模板和思路
然后按题目类型顺序逐个类型过一遍算法题,强化各个类型的特定模式
当遇到不熟悉的模式识别环节,就做一下特定模式识别环节的强化练习
相关文章:

刷题总结 回溯算法
为了方便复习并且在把算法忘掉的时候能尽量快速的捡起来 刷完回溯算法这里需要做个总结 回溯算法的适用范围 回溯算法是深度优先搜索(DFS)的一种特定应用,在DFS的基础上引入了约束检查和回退机制。 相比于普通的DFS,回溯法的优…...

C++ 静态变量static的使用方法
static概述: static关键字有三种使用方式,其中前两种只指在C语言中使用,第三种在C中使用。 静态局部变量(C) 静态全局变量/函数(C) 静态数据成员/成员函数(C) 静态局部变量 静态局部变量&…...
Langchain+文心一言调用
import osfrom langchain_community.llms import QianfanLLMEndpointos.environ["QIANFAN_AK"] "" os.environ["QIANFAN_SK"] ""llm_wenxin QianfanLLMEndpoint()res llm_wenxin.invoke("中国国庆日是哪一天?") print(…...

20250124 Flink中 窗口开始时间和結束時間
增量聚合的 ProcessWindowFunction # ProcessWindowFunction 可以与 ReduceFunction 或 AggregateFunction 搭配使用, 使其能够在数据到达窗口的时候进行增量聚合。当窗口关闭时,ProcessWindowFunction 将会得到聚合的结果。 这样它就可以增量聚合窗口的…...
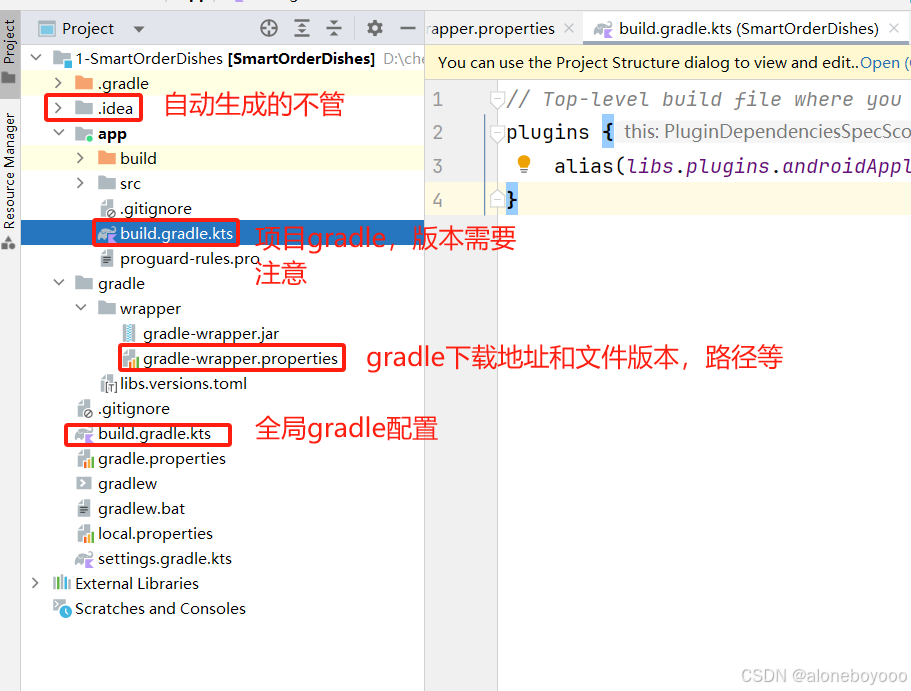
Android Studio安装配置
一、注意事项 想做安卓app和开发板通信,踩了大坑,Android 开发不是下载了就能直接开发的,对于新手需要注意的如下: 1、Android Studio版本,根据自己的Android Studio版本对应决定了你所兼容的AGP(Android…...
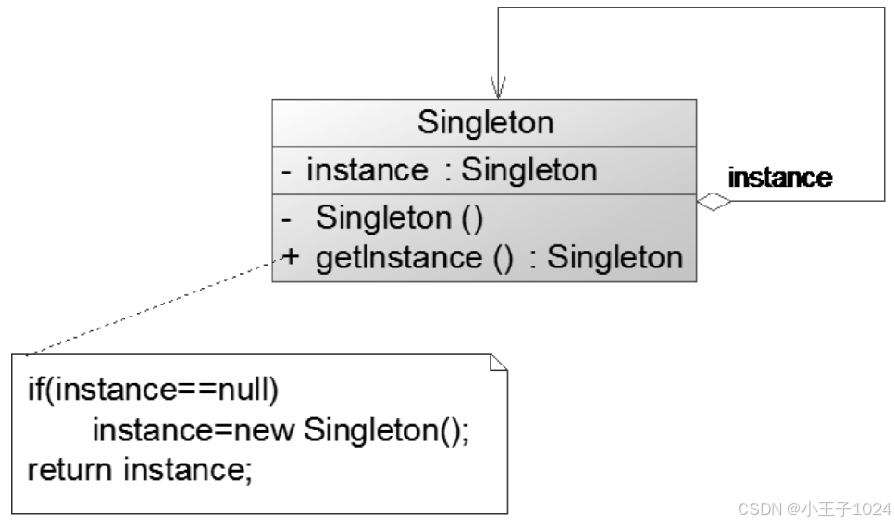
设计模式Python版 单例模式
文章目录 前言一、单例模式二、单例模式实现方式三、单例模式示例四、单例模式在Django框架的应用 前言 GOF设计模式分三大类: 创建型模式:关注对象的创建过程,包括单例模式、简单工厂模式、工厂方法模式、抽象工厂模式、原型模式和建造者模…...
7-Zip高危漏洞CVE-2025-0411:解析与修复
7-Zip高危漏洞CVE-2025-0411:解析与修复 免责声明 本系列工具仅供安全专业人员进行已授权环境使用,此工具所提供的功能只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利…...
python实现http文件服务器访问下载
//1.py import http.server import socketserver import os import threading import sys# 获取当前脚本所在的目录 DIRECTORY os.path.dirname(os.path.abspath(__file__))# 设置服务器的端口 PORT 8000# 自定义Handler,将根目录设置为脚本所在目录 class MyHTT…...
—— 容灾与备份)
《一文讲透》第4期:KWDB 数据库运维(6)—— 容灾与备份
一、KWDB 容灾 WAL 概述 KWDB 采用预写式日志(Write-Ahead Logging,WAL),记录每个时序表的模式变更和数据变更,以实现时序数据库的数据灾难恢复、时序数据的一致性和原子性。 KWDB 默认会将保存在 WAL 日志缓存中的…...
ArcGIS10.2 许可License点击始终启动无响应的解决办法及正常启动的前提
1、问题描述 在ArcGIS License Administrator中,手动点击“启动”无响应;且在计算机管理-服务中,无ArcGIS License 或者License的启动、停止、禁止等均为灰色,无法操作。 2、解决方法 ①通过cmd对service.txt进行手动服务的启动…...

Level2逐笔成交逐笔委托毫秒记录:今日分享优质股票数据20250124
逐笔成交逐笔委托下载 链接: https://pan.baidu.com/s/1UWVY11Q1IOfME9itDN5aZA?pwdhgeg 提取码: hgeg Level2逐笔成交逐笔委托数据分享下载 通过Level2逐笔成交与逐笔委托的详细数据,这种以毫秒为单位的信息能揭示许多关键点,如庄家意图、误导性行为…...
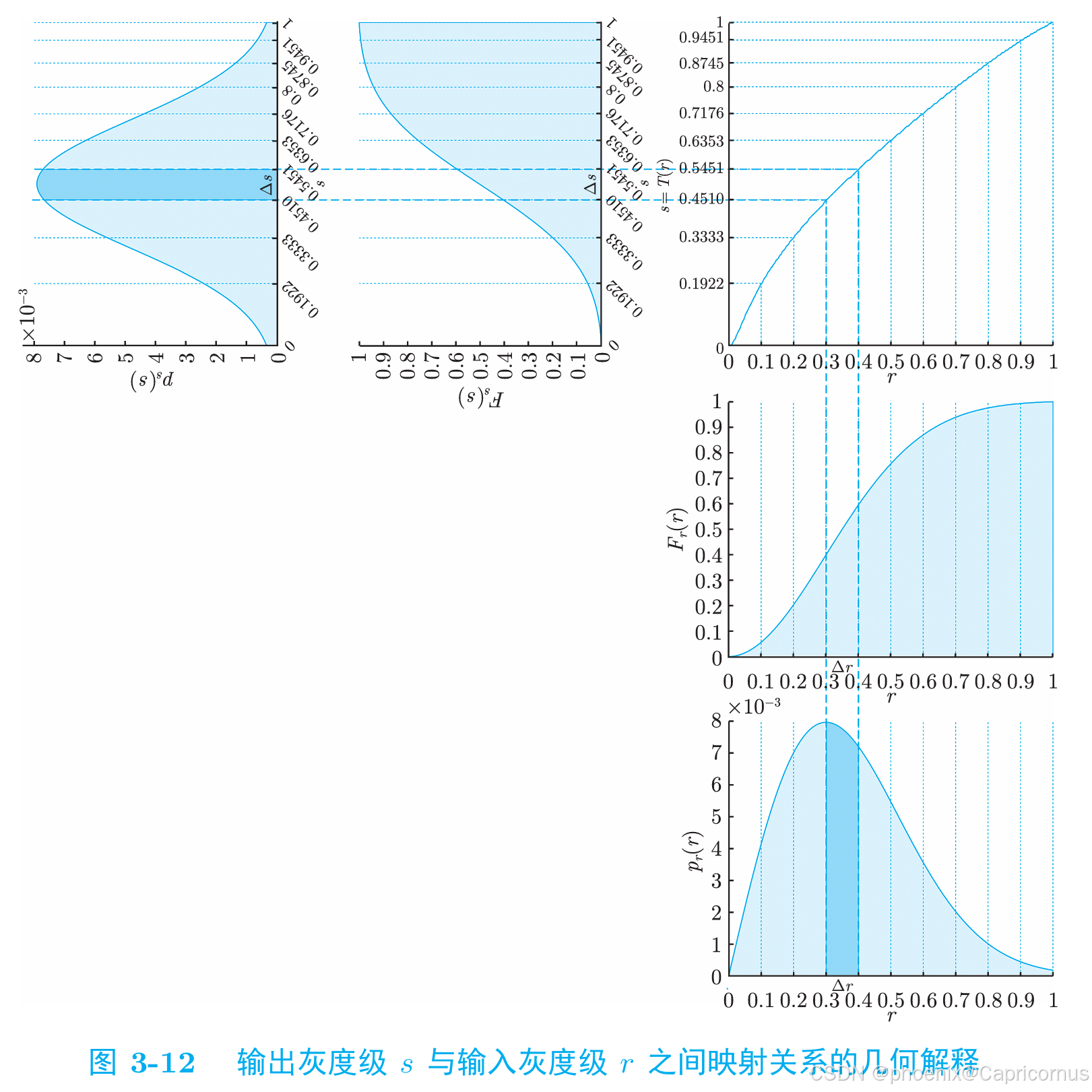
概率密度函数(PDF)分布函数(CDF)——直方图累积直方图——直方图规定化的数学基础
对于连续型随机变量,分布函数(Cumulative Distribution Function, CDF)是概率密度函数(Probability Density Function, PDF)的变上限积分,概率密度函数是分布函数的导函数。 如果我们有一个连续型随机变量…...
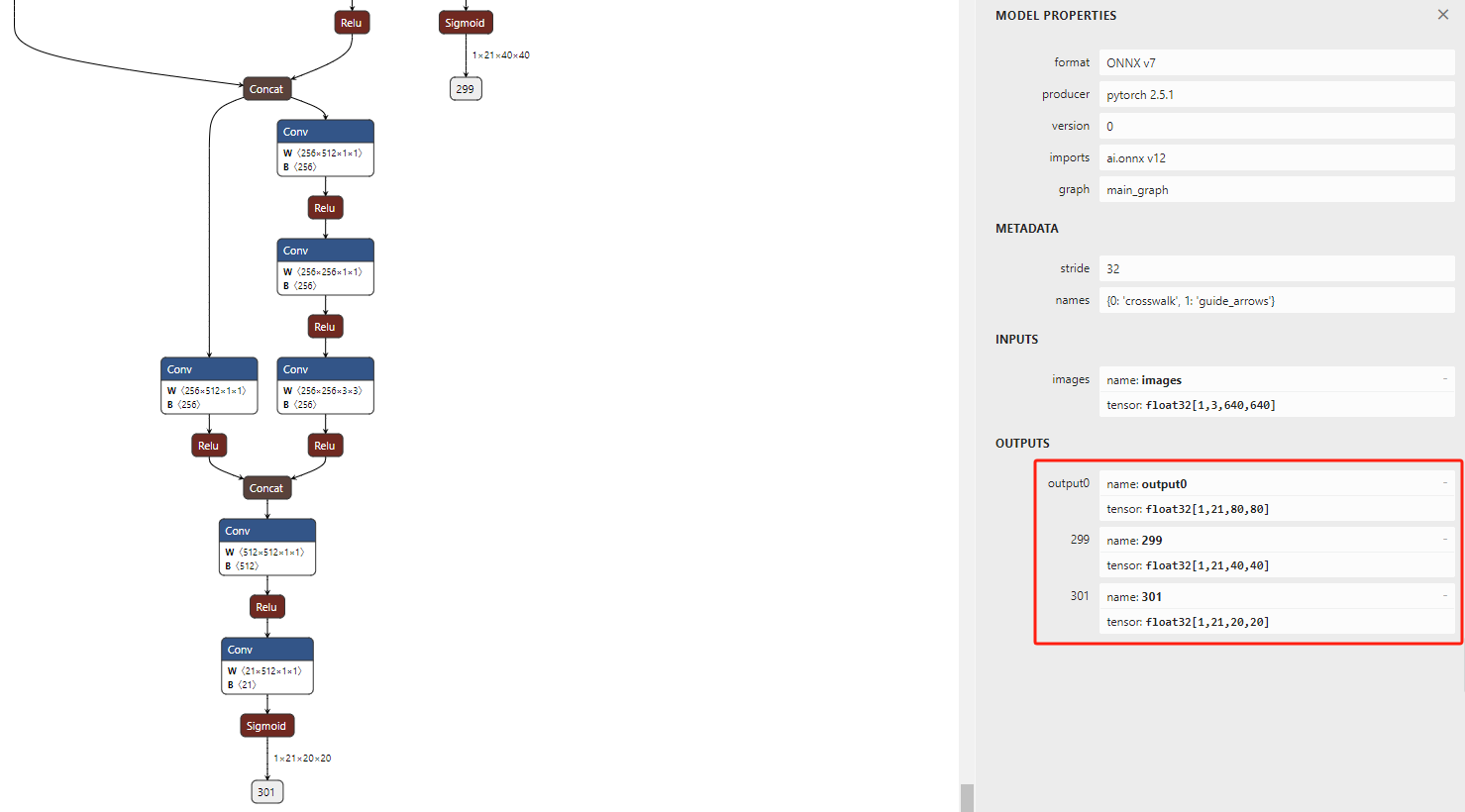
YOLOv5训练自己的数据及rknn部署
YOLOv5训练自己的数据及rknn部署 一、下载源码二、准备自己的数据集2.1 标注图像2.2 数据集结构 三、配置YOLOv5训练3.1 修改配置文件3.2 模型选择 四、训练五、测试六、部署6.1 pt转onnx6.2 onnx转rknn 七、常见错误7.1 训练过程中的错误7.1.1 cuda: out of memory7.1.2 train…...

计算机图形学:实验四 带纹理的OBJ文件读取和显示
一、程序功能设计 在程序中读取带纹理的obj文件,载入相应的纹理图片文件,将带纹理的模型显示在程序窗口中。实现带纹理的OBJ文件读取与显示功能,具体设计如下: OBJ文件解析与数据存储 通过实现TriMesh类中的readObj函数&#x…...

SQL Server 使用SELECT INTO实现表备份
在数据库管理过程中,有时我们需要对表进行备份,以防数据丢失或修改错误。在 SQL Server 中,可以使用 SELECT INTO 语句将数据从一个表备份到另一个表。 备份表的 SQL 语法: SELECT * INTO 【备份表名】 FROM 【要备份的表】 SEL…...
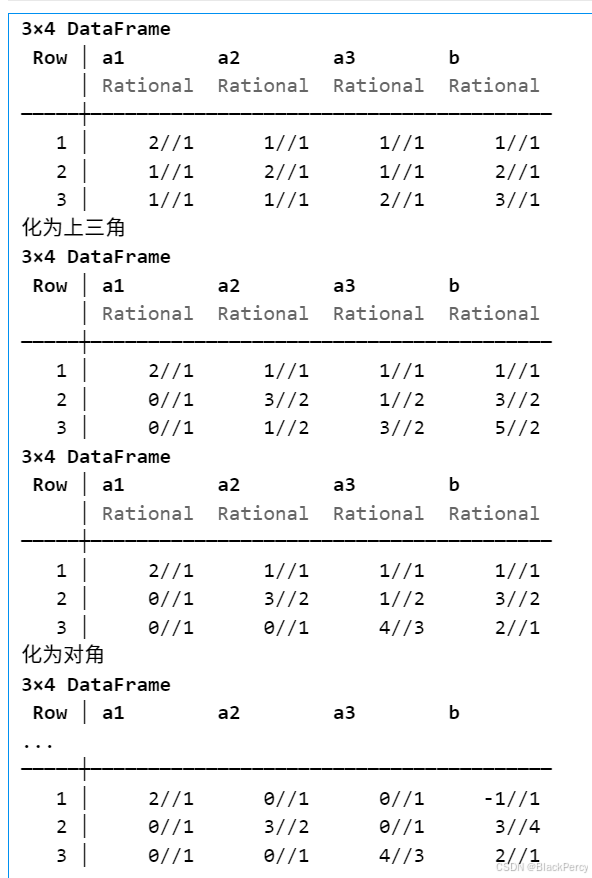
【线性代数】基础版本的高斯消元法
[精确算法] 高斯消元法求线性方程组 线性方程组 考虑线性方程组, 已知 A ∈ R n , n , b ∈ R n A\in \mathbb{R}^{n,n},b\in \mathbb{R}^n A∈Rn,n,b∈Rn, 求未知 x ∈ R n x\in \mathbb{R}^n x∈Rn A 1 , 1 x 1 A 1 , 2 x 2 ⋯ A 1 , n x n b 1…...

Python标准库 threading 的 start 和 join 的使用
python 的多线程机制可以的适用场景不适合与计算密集型的,因为 GIL 的存在,多线程在处理计算密集型时,实际上也是串行的,因为每个时刻只有一个线程可以获得 GIL,但是对于 IO 处理来说,不管是网络IO还是文件…...
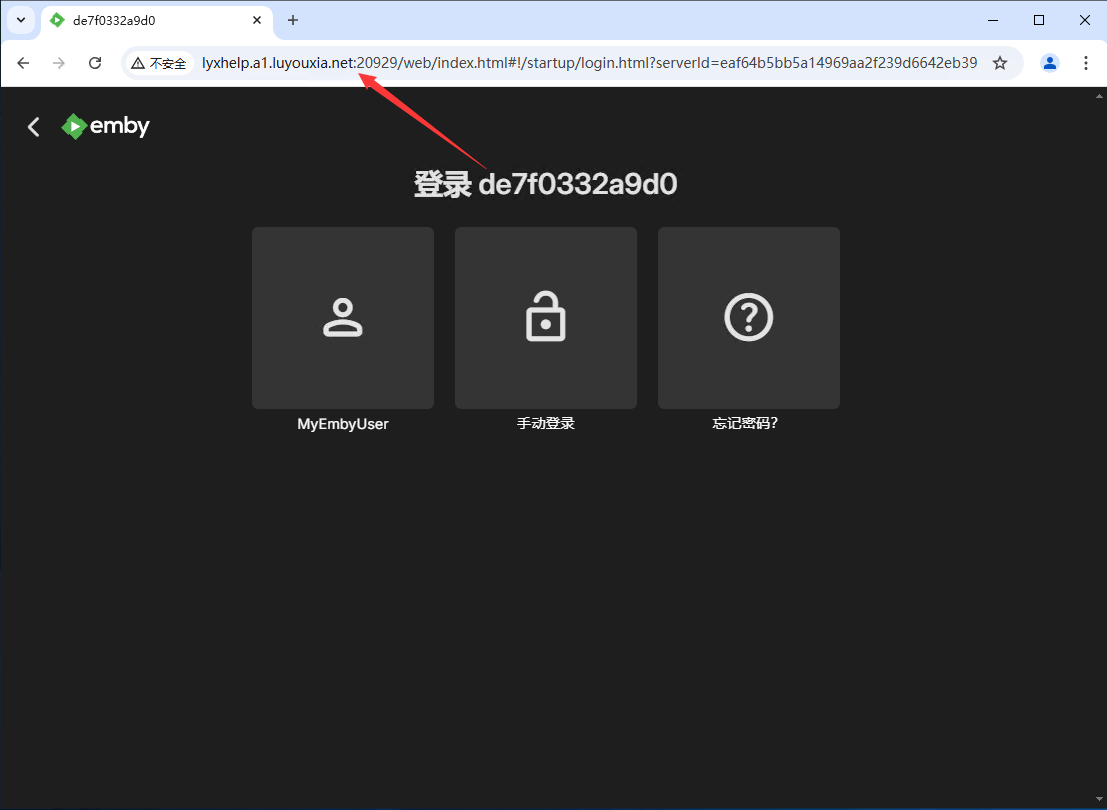
无公网IP 外网访问媒体服务器 Emby
Emby 是一款多媒体服务器软件,用户可以在 Emby 创建自己的个人多媒体娱乐中心,并且可以跨多个设备访问自己的媒体库。它允许用户管理传输自己的媒体内容,比如电影、电视节目、音乐和照片等。 本文将详细的介绍如何利用 Docker 在本地部署 Emb…...
【数据结构】_顺序表
目录 1. 概念与结构 1.1 静态顺序表 1.2 动态顺序表 2. 动态顺序表实现 2.1 SeqList.h 2.2 SeqList.c 2.3 Test_SeqList.c 3. 顺序表性能分析 线性表是n个具有相同特性的数据元素的有限序列。 常见的线性表有:顺序表、链表、栈、队列、字符串等;…...

[MySQL]数据库表内容的增删查改操作大全
目录 一、增加表数据 1.全列插入与指定列插入 2.多行数据插入 3.更新与替换插入 二、查看表数据 1.全列查询与指定列查询 2.查询表达式字段 3.为查询结果起别名 4.结果去重 5.WHERE条件 6.结果排序 7.筛选分页结果 8.插入查询的结果 9.group by子句 三、修改表数…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
