【线性代数】基础版本的高斯消元法
[精确算法] 高斯消元法求线性方程组
线性方程组
考虑线性方程组, 已知 A ∈ R n , n , b ∈ R n A\in \mathbb{R}^{n,n},b\in \mathbb{R}^n A∈Rn,n,b∈Rn, 求未知 x ∈ R n x\in \mathbb{R}^n x∈Rn
A 1 , 1 x 1 + A 1 , 2 x 2 + ⋯ + A 1 , n x n = b 1 , A_{1,1} x_1 +A_{1,2}x_2+\cdots +A_{1,n} x_n = b_1, A1,1x1+A1,2x2+⋯+A1,nxn=b1,
A 2 , 1 x 1 + A 2 , 2 x 2 + ⋯ + A 2 , n x n = b 2 , A_{2,1} x_1 +A_{2,2}x_2 +\cdots +A_{2,n} x_n = b_2, A2,1x1+A2,2x2+⋯+A2,nxn=b2,
⋯ \cdots ⋯
A n , 1 x 1 + A n , 2 x 2 + ⋯ + A n , n x n = b n , A_{n,1} x_1 +A_{n,2}x_2 +\cdots +A_{n,n} x_n = b_n, An,1x1+An,2x2+⋯+An,nxn=bn,
也可以写为矩阵乘法的形式,
A x = b Ax=b Ax=b
化为上三角
-
第 1 轮:
A i , 1 : n = A i , 1 : n − A i , 1 A 1 , 1 A 1 , 1 : n , i = 2 , ⋯ , n A_{i,1:n} = A_{i,1:n}- \frac{A_{i,1}}{A_{1,1}} A_{1,1:n}, i=2,\cdots,n Ai,1:n=Ai,1:n−A1,1Ai,1A1,1:n,i=2,⋯,n -
第 2 轮:
A i , 2 : n = A i , 2 : n − A i , 2 A 2 , 2 A 2 , 2 : n , i = 3 , ⋯ , n A_{i,2:n} = A_{i,2:n}- \frac{A_{i,2}}{A_{2,2}} A_{2,2:n}, i=3,\cdots,n Ai,2:n=Ai,2:n−A2,2Ai,2A2,2:n,i=3,⋯,n
⋯ \cdots ⋯ -
第 k 轮:
A i , k : n = A i , k : n − A i , k A k , k A k , k : n , i = k + 1 , ⋯ , n A_{i,k:n} = A_{i,k:n}- \frac{A_{i,k}}{A_{k,k}} A_{k,k:n}, i=k+1,\cdots,n Ai,k:n=Ai,k:n−Ak,kAi,kAk,k:n,i=k+1,⋯,n -
第n-1 轮
A i , n − 1 : n = A i , n − 1 : n − A i , n − 1 A n − 1 , n − 1 A n , n − 1 : n , i = n A_{i,n-1:n} = A_{i,n-1:n} - \frac{A_{i, n-1}}{A_{n-1,n-1}} A_{n,n-1:n}, i=n Ai,n−1:n=Ai,n−1:n−An−1,n−1Ai,n−1An,n−1:n,i=n
化为对角
-
第 1 轮:
A i , 2 : n = A i , 2 : n − A i , n A n , n A n , 2 : n , i = 1 , ⋯ , n − 1 A_{i,2:n} = A_{i,2:n}- \frac{A_{i,n}}{A_{n,n}} A_{n,2:n}, i=1,\cdots,n-1 Ai,2:n=Ai,2:n−An,nAi,nAn,2:n,i=1,⋯,n−1 -
第 2 轮:
A i , 2 : n − 1 = A i , 2 : n − 1 − A i , n − 1 A n − 1 , n − 1 A n − 1 , 2 : n − 1 , i = 1 , ⋯ , n − 2 A_{i,2:n-1} = A_{i,2:n-1}- \frac{A_{i,n-1}}{A_{n-1,n-1}} A_{n-1,2:n-1}, i=1,\cdots,n-2 Ai,2:n−1=Ai,2:n−1−An−1,n−1Ai,n−1An−1,2:n−1,i=1,⋯,n−2
⋯ \cdots ⋯ -
第 k 轮:
A i , 2 : n − k + 1 = A i , 2 : n − k + 1 − A i , n − k + 1 A n − k + 1 , n − k + 1 A n − k + 1 , 2 : n − k + 1 , i = 1 , ⋯ , n − k + 1 A_{i,2:n-k+1} = A_{i,2:n-k+1}- \frac{A_{i,n-k+1}}{A_{n-k+1,n-k+1}} A_{n-k+1,2:n-k+1}, i=1,\cdots,n-k+1 Ai,2:n−k+1=Ai,2:n−k+1−An−k+1,n−k+1Ai,n−k+1An−k+1,2:n−k+1,i=1,⋯,n−k+1 -
第n-1 轮
A i , 2 = A i , 2 − A i , 2 A 2 , 2 A 2 , 2 , i = 1 A_{i,2} = A_{i,2} - \frac{A_{i, 2}}{A_{2,2}} A_{2,2}, i=1 Ai,2=Ai,2−A2,2Ai,2A2,2,i=1
美化数据格式
using DataFrames
function pm(A,b)m,n=size(A); z=[]for i=1:nz=[z; "a$i"]endz=[z; "b"]println(DataFrame([A b],z))
end
高斯消元法程序
function LEsol(A,b,SHOW=false)"""SHOW 默认为 false 不输出解题步骤, 可以选填 true 输出解题步骤"""n=length(b); A=copy(A); b=copy(b)if SHOW pm(A,b) endif SHOW println("化为上三角") endfor i=1:n-1for j=i+1:nc=A[j,i]/A[i,i]b[j]=b[j]-b[i]*cA[j,i:n]=A[j,i:n]-A[i,i:n]*c endif SHOW pm(A,b) endendif SHOW println("化为对角") endfor i=n:-1:2for j=1:i-1c=A[j,i]/A[i,i]b[j]=b[j]-b[i]*cA[j,i:n]=A[j,i:n]-A[i,i:n]*cendif SHOW pm(A,b) endendx=copy(b)for j=1:nx[j]=b[j]/A[j,j];endreturn(x)
end
举例
n=3;
A=ones(Rational,n,n)
b=ones(Rational,n)
for i=1:n-1A[i,i]=2.0;A[i,i+1]=1.0;A[i+1,i]=1.0; b[i]=i+0.0
end
A[n,n]=2.0;
b[n]=n;
x=LEsol(A,b,true)
求解结果
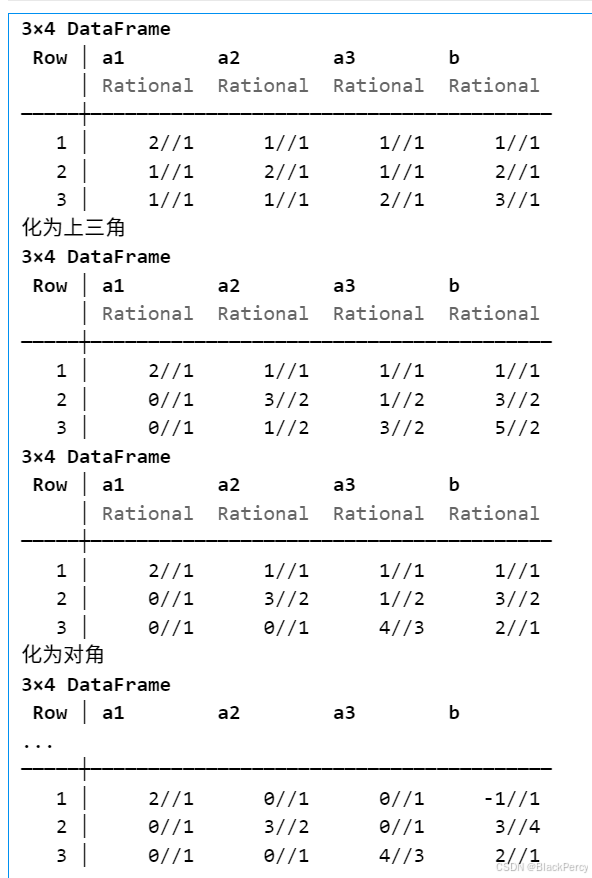
相关文章:

【线性代数】基础版本的高斯消元法
[精确算法] 高斯消元法求线性方程组 线性方程组 考虑线性方程组, 已知 A ∈ R n , n , b ∈ R n A\in \mathbb{R}^{n,n},b\in \mathbb{R}^n A∈Rn,n,b∈Rn, 求未知 x ∈ R n x\in \mathbb{R}^n x∈Rn A 1 , 1 x 1 A 1 , 2 x 2 ⋯ A 1 , n x n b 1…...

Python标准库 threading 的 start 和 join 的使用
python 的多线程机制可以的适用场景不适合与计算密集型的,因为 GIL 的存在,多线程在处理计算密集型时,实际上也是串行的,因为每个时刻只有一个线程可以获得 GIL,但是对于 IO 处理来说,不管是网络IO还是文件…...
无公网IP 外网访问媒体服务器 Emby
Emby 是一款多媒体服务器软件,用户可以在 Emby 创建自己的个人多媒体娱乐中心,并且可以跨多个设备访问自己的媒体库。它允许用户管理传输自己的媒体内容,比如电影、电视节目、音乐和照片等。 本文将详细的介绍如何利用 Docker 在本地部署 Emb…...
【数据结构】_顺序表
目录 1. 概念与结构 1.1 静态顺序表 1.2 动态顺序表 2. 动态顺序表实现 2.1 SeqList.h 2.2 SeqList.c 2.3 Test_SeqList.c 3. 顺序表性能分析 线性表是n个具有相同特性的数据元素的有限序列。 常见的线性表有:顺序表、链表、栈、队列、字符串等;…...

[MySQL]数据库表内容的增删查改操作大全
目录 一、增加表数据 1.全列插入与指定列插入 2.多行数据插入 3.更新与替换插入 二、查看表数据 1.全列查询与指定列查询 2.查询表达式字段 3.为查询结果起别名 4.结果去重 5.WHERE条件 6.结果排序 7.筛选分页结果 8.插入查询的结果 9.group by子句 三、修改表数…...

解决双系统引导问题:Ubuntu 启动时不显示 Windows 选项的处理方法
方法 1:检查 GRUB 引导菜单是否隐藏 启动进入 Ubuntu 系统。打开终端,输入以下命令编辑 GRUB 配置文件:sudo nano /etc/default/grub检查以下配置项: GRUB_TIMEOUT0:如果是 0,将其改为一个较大的值&#x…...
Java面试题2025-Spring
讲师:邓澎波 Spring面试专题 1.Spring应该很熟悉吧?来介绍下你的Spring的理解 1.1 Spring的发展历程 先介绍Spring是怎么来的,发展中有哪些核心的节点,当前的最新版本是什么等 通过上图可以比较清晰的看到Spring的各个时间版本对…...

CentOS7安装使用containerd
一,安装 1.1、安装containerd 下载 https://github.com/containerd/containerd/releases/download/v1.7.24/cri-containerd-cni-1.7.24-linux-amd64.tar.gz wget https://github.com/containerd/containerd/releases/download/v1.7.24/cri-containerd-cni-1.7.24-…...

Redis 集群模式入门
Redis 集群模式入门 一、简介 Redis 有三种集群模式:主从模式、Sentinel 哨兵模式、cluster 分片模式 主从复制(Master-Slave Replication): 在这种模式下,数据可以从一个 Redis 实例(主节点 Master)复…...

WinDBG查找C++句柄泄露
C代码(频繁点击About按钮导致Mutex句柄泄露) HANDLE _mutexHandle;LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam) {switch (message){case WM_COMMAND:{int wmId LOWORD(wParam);// 分析菜单选择:switch (wmId){c…...

Linux查看服务器的内外网地址
目录: 1、内网地址2、外网地址3、ping时显示地址与真实不一致 1、内网地址 ifconfig2、外网地址 curl ifconfig.me3、ping时显示地址与真实不一致 原因是dns缓存导致的,ping这种方法也是不准确的,有弊端不建议使用,只适用于测试…...

深入MapReduce——引入
引入 前面我们已经深入了HDFS的设计与实现,对于分布式系统也有了不错的理解。 但HDFS仅仅解决了海量数据存储和读写的问题。要想让数据产生价值,一定是需要从数据中挖掘出价值才行,这就需要我们拥有海量数据的计算处理能力。 下面我们还是…...

Oracle之开窗函数使用
Oracle中的开窗函数(Window Functions)是一种强大的工具,用于在SQL查询中对数据进行复杂的分析和聚合操作,而无需改变原始查询结果的行数或顺序。以下是关于Oracle开窗函数的使用方法和常见示例: 1. 开窗函数的基本语法…...
)
航空客户价值的数据挖掘与分析(numpy+pandas+matplotlib+scikit-learn)
文章目录 航空客户价值的数据挖掘与分析(numpy+pandas+matplotlib+scikit-learn)写在前面背景与挖掘目标1.1 需求背景1.2 挖掘目标1.3 项目概述项目分析方法规划2.1 RFM模型2.2 LRFMC模型指标2.3 分析总体流程图数据抽取探索及预处理3.1 数据抽取3.2 数据探索分析3.3 数据预处…...

云原生时代,如何构建高效分布式监控系统
文章目录 一.监控现状二.Thanos原理分析SidecarQuerierStoreCompactor 三.Sidecar or ReceiverThanos Receiver工作原理 四.分布式运维架构 一.监控现状 Prometheus是CNCF基金会管理的一个开源监控项目,由于其良好的架构设计和完善的生态,迅速成为了监控…...

什么是CIDR技术? 它是如何解决路由缩放问题的
什么是CIDR技术? 它是如何解决路由缩放问题的 一. 什么是 CIDR?二. CIDR 是如何工作的?1. 高效地址分配2. 路由聚合(Route Aggregation)3. 精确满足需求 三. CIDR 的计算详解1. 子网掩码计算2. 地址范围计算3. 可用 IP…...

Unity URP 获取/设置 Light-Indirect Multiplier
Unity URP 获取/设置 Light-Indirect Multiplier 他喵的代码的字段名称叫:bounceIntensity ~~~~~~...

用Python和Tkinter标准模块建立密码管理器
用Python和Tkinter标准模块建立密码管理器 创建一个简单的密码管理器应用程序,帮助用户存储和管理他们的密码。使用Python的tkinter模块来创建一个图形用户界面(GUI)。 本程序支持 添加、查看、搜索、复制、修改、删除 功能。 本程序使用 …...

PyQt5菜单加多页签实现
pyqt tabs标签_哔哩哔哩_bilibili 代码实现 # coding:utf-8 import sys from PyQt5.QtCore import Qt from PyQt5 import QtCore,QtWidgets from PyQt5.QtWidgets import QApplication,QWidget from QhTabs01 import Ui_Form from PyQt5.Qt import *class QhLiangHuaGUI(QWidg…...

关注搜索引擎蜘蛛压力
以前在建站的时候,他们说蜘蛛来抓取的频率越多越好,因为蜘蛛来抓取说明了网站更新速度快,受搜索引擎的欢迎,但是在最近的网站统计中,发现很多蜘蛛爬取的频次非常的高,比如有的蜘蛛一天能来网站几万次&#…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
