Hive之加载csv格式数据到hive
场景:
今天接了一个需求,将测试环境的hive数据导入到正式环境中。但是不需要整个流程的迁移,只需要迁移ads表
解决方案:
拿到这个需求首先想到两个方案:
1、将数据通过insert into语句导出,然后运行脚本
2、数据导出成csv格式的数据,然后Load进hive
方案一的实践过程中,发现几个问题,然后果断进行了方案二。就讲讲方案一存在的问题
- ads数据量较大。存在18W的数据量,对于大集群而言不值一提,但是公司的堡垒机资源较小,且用DBServer不支持18WSQL执行
- DBServer hive不支持SQL脚本运行,只能粘贴复制,还是问题一一样资源太小
最终采用方案二
实践过程:
这里就说说方案二遇到的问题以及解决方案
-
hive查询结果导出CSV时间格式问题。下图就我设置了CSV导出格式,但是还是存在问题,且时间格式还存在引号的情况,所以将数据导出来之后,用WPS进行打开,对时间格式进行一个调整,然后在保存为CSV结构的数据,用nodepad++打开即可

-
hive导入成功但数据不存在。下面截图就展示了存在的问题。这个问题就是因为hive建表的问题,hive建表的格式不是文本格式导致的。我开始用的org.apache.hadoop.hive.ql.io.parquet.MapredParquetInputFormat,后续如果不指定格式,默认格式就是org.apache.hadoop.mapred.TextInputFormat即可导入进去


-
hive数据导入之后一行的数据都存在某一个字段中。这个问题是因为hive没有指定数据导入后按照什么方式进行分割。
SET SERDEPROPERTIES ('field.delim'=',', 'serialization.format'=' ')指定这个参数后,hive会将csv导入的数据按照逗号分隔。但是请注意,你的数据存在json数据或者别的逗号数据,导入后可能会产生数据错位的情况。在条件允许的情况下,将json和数据中的逗号,在WPS中用中文逗号替换即可。 -
其他的解决方案:其实这种类型的问题解决方案应该很多。例如:shell脚本执行hive insert语句、将数据插入到mysql用ETL的方式抽取到hive目标表。
总结:
导入数据考验一个细心的程度其实问题也不难,就是麻烦。如果其他网友有更好的解决办法,欢迎留言
相关文章:

Hive之加载csv格式数据到hive
场景: 今天接了一个需求,将测试环境的hive数据导入到正式环境中。但是不需要整个流程的迁移,只需要迁移ads表 解决方案: 拿到这个需求首先想到两个方案: 1、将数据通过insert into语句导出,然后运行脚本 …...

Java web与Java中的Servlet
一。前言 Java语言大多用于开发web系统的后端,也就是我们是的B/S架构。通过浏览器一个URL去访问系统的后端资源和逻辑。 当我在代码里看到这个类HttpServletRequest 时 让我想到了Servlet,Servlet看上去多么像是Java的一个普通类,但是它确实…...

kafka常用目录文件解析
文章目录 1、消息日志文件(.log)2、消费者偏移量文件(__consumer_offsets)3、偏移量索引文件(.index)4、时间索引文件( .timeindex)5、检查点引文件( .checkpoint&#x…...
RV1126+FFMPEG推流项目源码
源码在我的gitee上面,感兴趣的可以自行了解 nullhttps://gitee.com/x-lan/rv126-ffmpeg-streaming-projecthttps://gitee.com/x-lan/rv126-ffmpeg-streaming-project...

ANSYS SimAI
ANSYS SimAI 是 ANSYS 公司推出的一款基于人工智能(AI)的仿真解决方案,旨在通过机器学习技术加速仿真流程,降低计算资源需求,并为用户提供更高效的工程决策支持。其核心目标是简化复杂仿真过程,帮助工程师快…...
hedfs和hive数据迁移后校验脚本
先谈论校验方法,本人腾讯云大数据工程师。 1、hdfs的校验 这个通常就是distcp校验,hdfs通过distcp迁移到另一个集群,怎么校验你的对不对。 有人会说,默认会有校验CRC校验。我们关闭了,为什么关闭?全量迁…...

蓝桥杯单片机(八)定时器的基本原理与应用
模块训练: 当有长定时情况时,也就是定时长度超过65.5ms时,采用多次定时累加 一、定时器介绍 1.单片机的定时/计数器 2.定时器工作原理 3.定时器相关寄存器 二、定时器使用程序设计 1.程序设计思路 与写中断函数一样,先写一个初…...
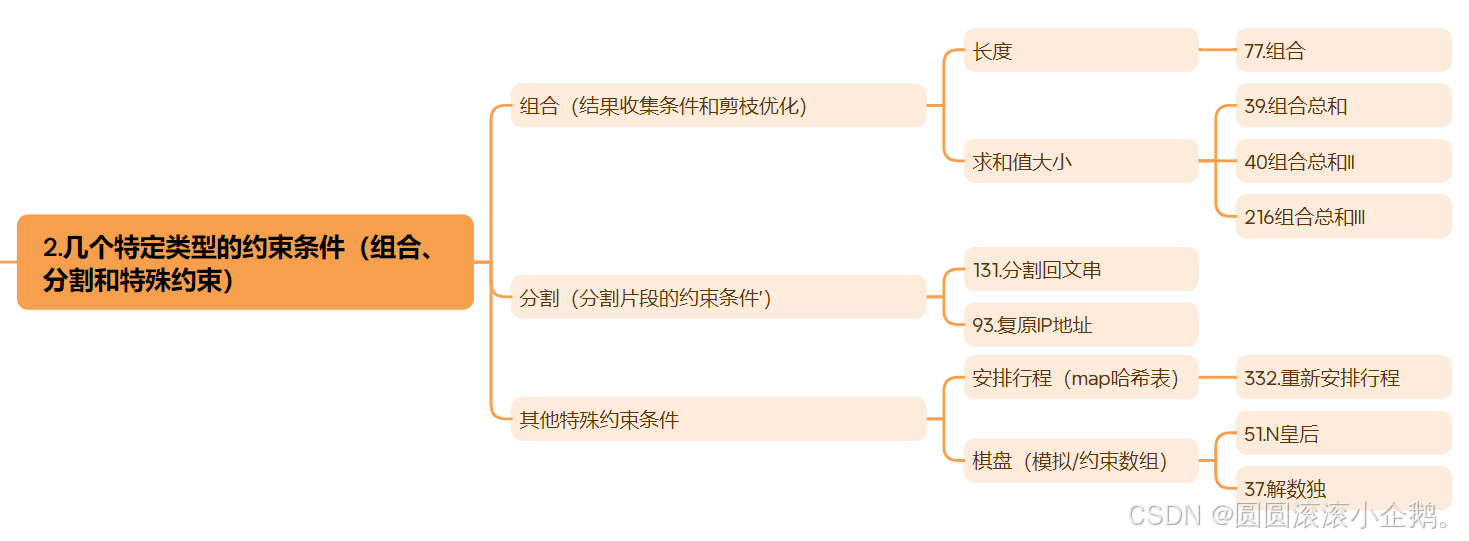
刷题总结 回溯算法
为了方便复习并且在把算法忘掉的时候能尽量快速的捡起来 刷完回溯算法这里需要做个总结 回溯算法的适用范围 回溯算法是深度优先搜索(DFS)的一种特定应用,在DFS的基础上引入了约束检查和回退机制。 相比于普通的DFS,回溯法的优…...

C++ 静态变量static的使用方法
static概述: static关键字有三种使用方式,其中前两种只指在C语言中使用,第三种在C中使用。 静态局部变量(C) 静态全局变量/函数(C) 静态数据成员/成员函数(C) 静态局部变量 静态局部变量&…...
Langchain+文心一言调用
import osfrom langchain_community.llms import QianfanLLMEndpointos.environ["QIANFAN_AK"] "" os.environ["QIANFAN_SK"] ""llm_wenxin QianfanLLMEndpoint()res llm_wenxin.invoke("中国国庆日是哪一天?") print(…...

20250124 Flink中 窗口开始时间和結束時間
增量聚合的 ProcessWindowFunction # ProcessWindowFunction 可以与 ReduceFunction 或 AggregateFunction 搭配使用, 使其能够在数据到达窗口的时候进行增量聚合。当窗口关闭时,ProcessWindowFunction 将会得到聚合的结果。 这样它就可以增量聚合窗口的…...
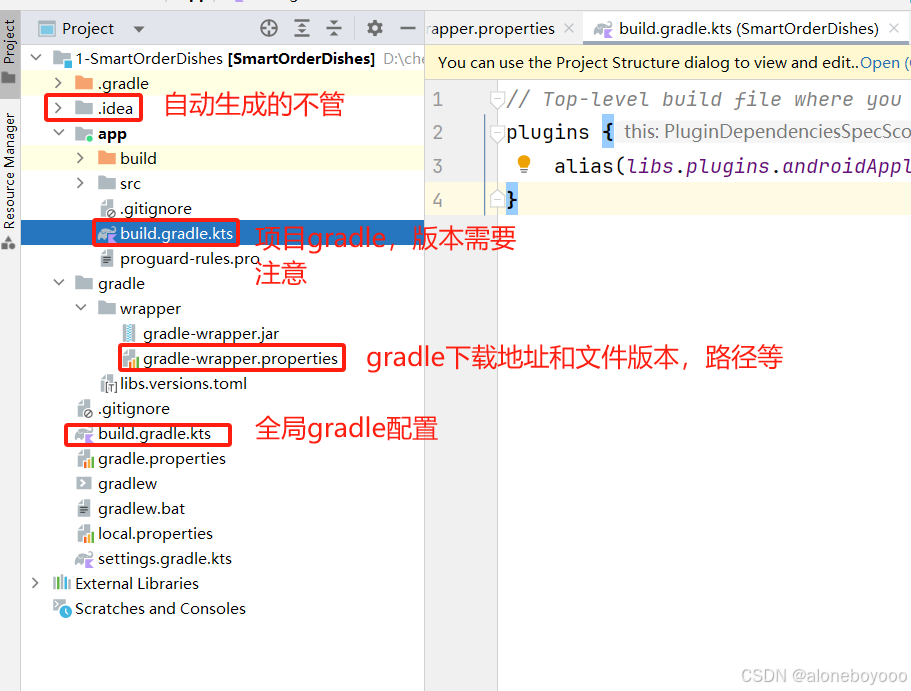
Android Studio安装配置
一、注意事项 想做安卓app和开发板通信,踩了大坑,Android 开发不是下载了就能直接开发的,对于新手需要注意的如下: 1、Android Studio版本,根据自己的Android Studio版本对应决定了你所兼容的AGP(Android…...
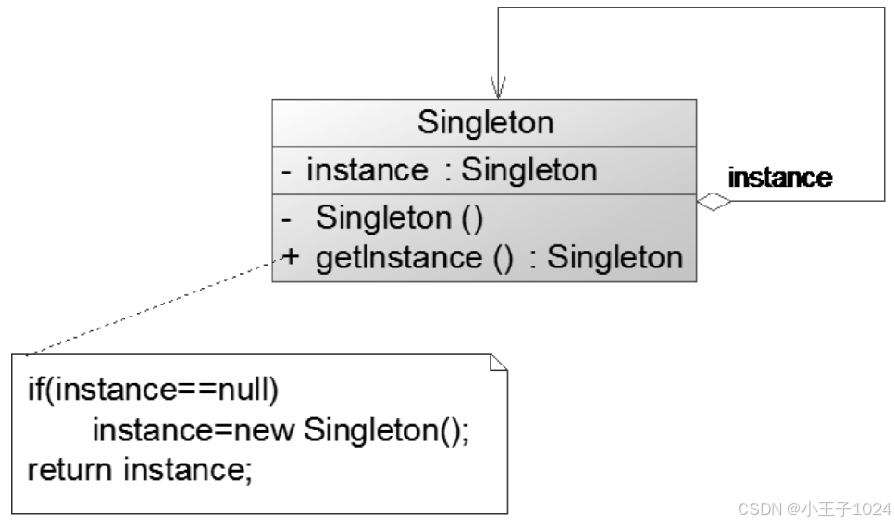
设计模式Python版 单例模式
文章目录 前言一、单例模式二、单例模式实现方式三、单例模式示例四、单例模式在Django框架的应用 前言 GOF设计模式分三大类: 创建型模式:关注对象的创建过程,包括单例模式、简单工厂模式、工厂方法模式、抽象工厂模式、原型模式和建造者模…...
7-Zip高危漏洞CVE-2025-0411:解析与修复
7-Zip高危漏洞CVE-2025-0411:解析与修复 免责声明 本系列工具仅供安全专业人员进行已授权环境使用,此工具所提供的功能只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利…...
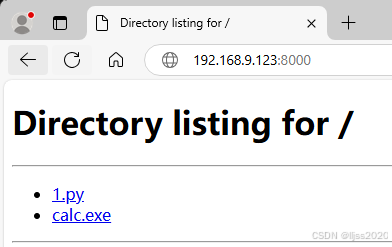
python实现http文件服务器访问下载
//1.py import http.server import socketserver import os import threading import sys# 获取当前脚本所在的目录 DIRECTORY os.path.dirname(os.path.abspath(__file__))# 设置服务器的端口 PORT 8000# 自定义Handler,将根目录设置为脚本所在目录 class MyHTT…...
—— 容灾与备份)
《一文讲透》第4期:KWDB 数据库运维(6)—— 容灾与备份
一、KWDB 容灾 WAL 概述 KWDB 采用预写式日志(Write-Ahead Logging,WAL),记录每个时序表的模式变更和数据变更,以实现时序数据库的数据灾难恢复、时序数据的一致性和原子性。 KWDB 默认会将保存在 WAL 日志缓存中的…...
ArcGIS10.2 许可License点击始终启动无响应的解决办法及正常启动的前提
1、问题描述 在ArcGIS License Administrator中,手动点击“启动”无响应;且在计算机管理-服务中,无ArcGIS License 或者License的启动、停止、禁止等均为灰色,无法操作。 2、解决方法 ①通过cmd对service.txt进行手动服务的启动…...

Level2逐笔成交逐笔委托毫秒记录:今日分享优质股票数据20250124
逐笔成交逐笔委托下载 链接: https://pan.baidu.com/s/1UWVY11Q1IOfME9itDN5aZA?pwdhgeg 提取码: hgeg Level2逐笔成交逐笔委托数据分享下载 通过Level2逐笔成交与逐笔委托的详细数据,这种以毫秒为单位的信息能揭示许多关键点,如庄家意图、误导性行为…...
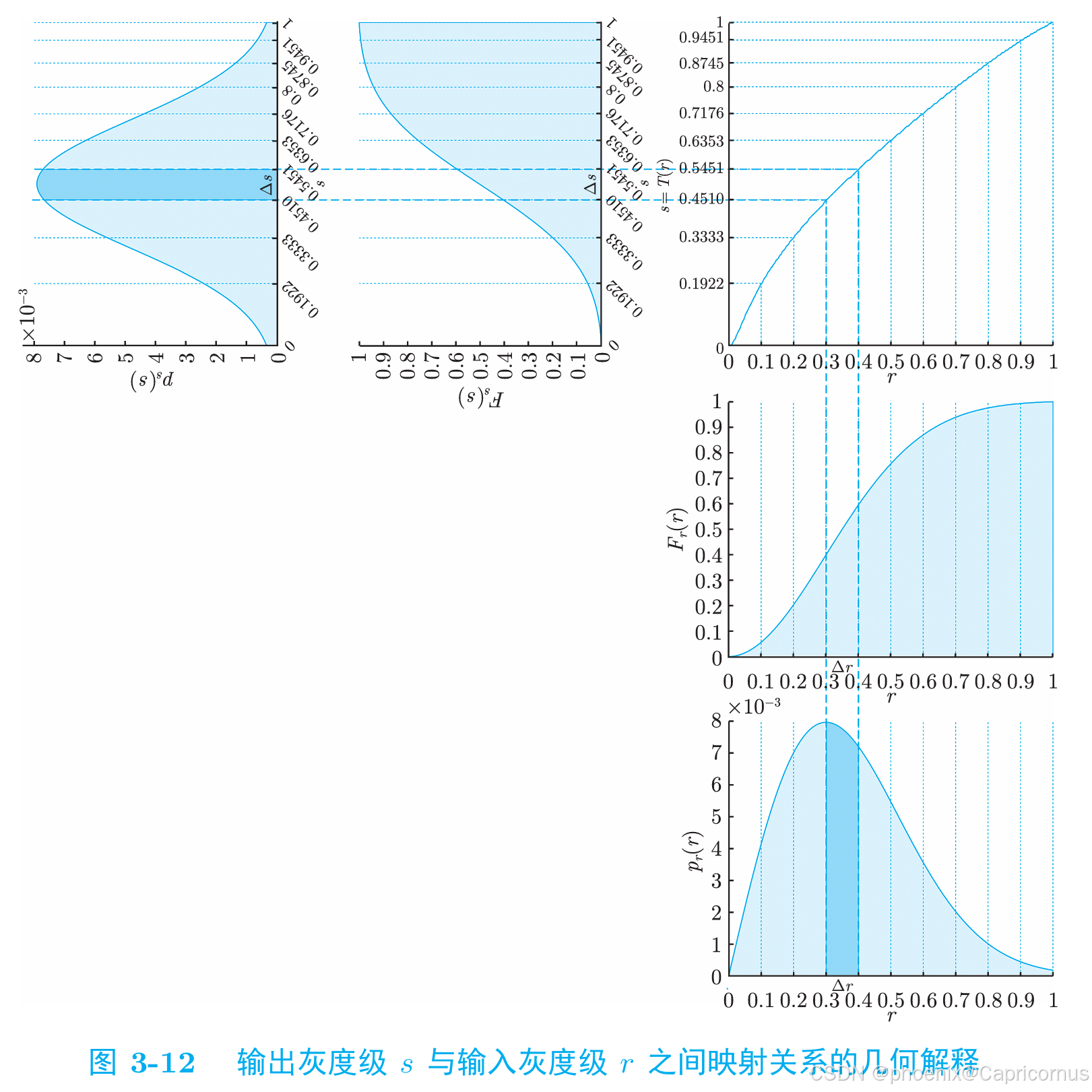
概率密度函数(PDF)分布函数(CDF)——直方图累积直方图——直方图规定化的数学基础
对于连续型随机变量,分布函数(Cumulative Distribution Function, CDF)是概率密度函数(Probability Density Function, PDF)的变上限积分,概率密度函数是分布函数的导函数。 如果我们有一个连续型随机变量…...
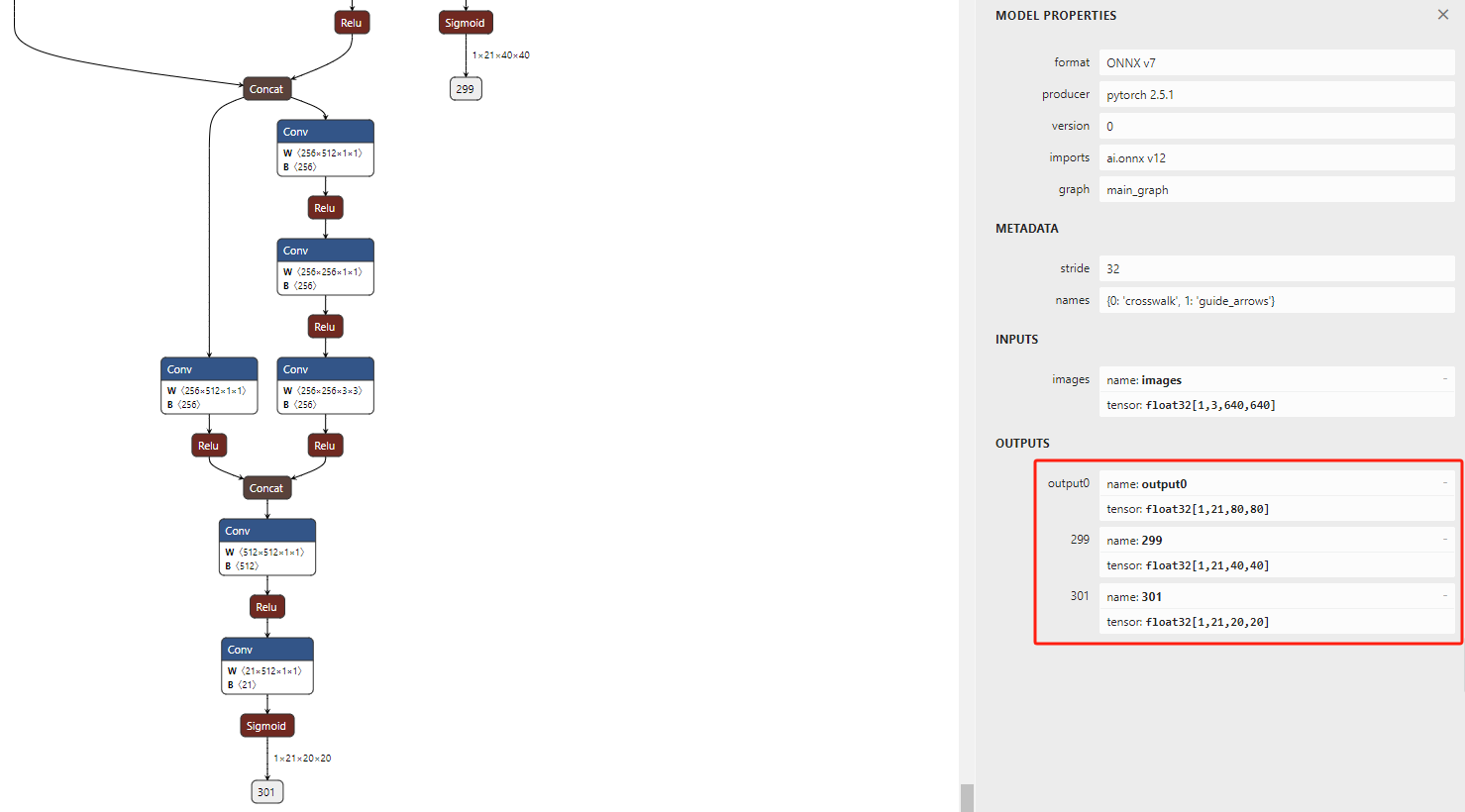
YOLOv5训练自己的数据及rknn部署
YOLOv5训练自己的数据及rknn部署 一、下载源码二、准备自己的数据集2.1 标注图像2.2 数据集结构 三、配置YOLOv5训练3.1 修改配置文件3.2 模型选择 四、训练五、测试六、部署6.1 pt转onnx6.2 onnx转rknn 七、常见错误7.1 训练过程中的错误7.1.1 cuda: out of memory7.1.2 train…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
