算法每日双题精讲 —— 二分查找(寻找旋转排序数组中的最小值,点名)
🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟
别再犹豫了!快来订阅我们的算法每日双题精讲专栏,一起踏上算法学习的精彩之旅吧💪

在算法的学习之旅中,二分查找是一种高效且经典的算法,其应用场景广泛。今天我们将深入探讨如何运用二分查找来解决 “寻找旋转排序数组中的最小值” 以及趣味十足的 “点名” 问题。这两道题不仅能加深我们对二分查找的理解,还能锻炼我们在不同场景下灵活运用算法的能力。
目录
一、寻找旋转排序数组中的最小值
📖题目描述
🧠讲解算法原理
💻代码实现(以 C++ 为例)
复杂度分析
二、点名
📖题目描述
🧠讲解算法原理
💻代码实现(以 C++ 为例)
复杂度分析
一、寻找旋转排序数组中的最小值
题目链接👉【力扣】
📖题目描述


🧠讲解算法原理
对于这道题,我们可以利用二分查找来优化时间复杂度。
初始化左指针 left 为 0,右指针 right 为数组长度减 1。在循环过程中,计算中间索引 mid = left + (right - left) / 2 。
比较 nums[mid] 与 nums[right] 的大小:
- 如果 nums[mid] < nums[right] ,说明最小值在 mid 及其左边,因为 mid 到 right 这一段是有序的,最小值肯定不在这一段,所以将 right 更新为 mid 。
- 如果 nums[mid] > nums[right] ,说明最小值在 mid 的右边,因为 mid 及其左边这一段是有序的,最小值不在这一段,所以将 left 更新为 mid + 1 。
当 left 等于 right 时,循环结束,此时 nums[left] 就是数组中的最小值。

💻代码实现(以 C++ 为例)
#include <iostream>
#include <vector>using namespace std;int findMin(vector<int>& nums) {int left = 0, right = nums.size() - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] < nums[right]) {right = mid;}else {left = mid + 1;}}return nums[left];
}复杂度分析
- 时间复杂度:每次循环都将搜索区间缩小一半,所以时间复杂度为
,其中
是数组的长度。相比遍历整个数组查找最小值的暴力解法(时间复杂度为
),效率大大提高。
- 空间复杂度:只使用了常数级别的额外空间,即几个指针变量,所以空间复杂度为
。
二、点名
题目链接👉【力扣】
📖题目描述


🧠讲解算法原理
这道题同样可以借助二分查找来高效解决。
初始化左指针 left 为 0,右指针 right 为名单长度减 1。
在循环中,计算中间索引 mid = left + (right - left) / 2 。
比较中间位置的学生名字与老师点的名字:
- 如果相同,直接返回 mid 。
- 如果中间位置的名字小于老师点的名字,说明要找的名字在 mid 的右边,将 left 更新为 mid + 1 。
- 如果中间位置的名字大于老师点的名字,说明要找的名字在 mid 的左边,将 right 更新为 mid - 1 。
当 left 大于 right 时,循环结束,说明名单中没有该学生,返回 -1 。
💻代码实现(以 C++ 为例)
#include <iostream>
#include <vector>
#include <string>using namespace std;int rollCall(vector<string>& names, string target) {int left = 0, right = names.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (names[mid] == target) {return mid;}else if (names[mid] < target) {left = mid + 1;}else {right = mid - 1;}}return -1;
}复杂度分析
- 时间复杂度:每次迭代都能将搜索区间缩小一半,时间复杂度为
,其中
是名单中学生的数量。相比逐个遍历名单查找学生的暴力解法(时间复杂度为
),效率大幅提升。
- 空间复杂度:只使用了常数级别的额外空间,如几个指针变量,所以空间复杂度为
。
通过对这两道题目的学习,我们对二分查找算法的理解和应用能力又上了一个新台阶。在今后遇到类似问题时,要学会灵活运用二分查找来优化代码的时间复杂度。
如果大家在学习过程中有任何疑问或者想法,欢迎在评论区交流分享。后续我还会带来更多精彩的算法内容,记得关注哦!

相关文章:

算法每日双题精讲 —— 二分查找(寻找旋转排序数组中的最小值,点名)
🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟 别再犹豫了!快来订阅我们的算法每日双题精讲专栏,一起踏上算法学习的精彩之旅吧💪 在算法的…...

three.js+WebGL踩坑经验合集(4.2):为什么不在可视范围内的3D点投影到2D的结果这么不可靠
上一篇,笔者留下了一个问题,three.js内置的THREE.Vector3.project方法算出来的结果对于超出屏幕可见范围的点来说错得相当离谱。 three.jsWebGL踩坑经验合集(4.1):THREE.Line2的射线检测问题(注意本篇说的是Line2,同样也不是阈值…...
- kafka 查看kafka的运行状态、broker.id不一致导致启动失败问题、topic消息积压量告警监控脚本)
Kafka运维宝典 (二)- kafka 查看kafka的运行状态、broker.id不一致导致启动失败问题、topic消息积压量告警监控脚本
Kafka运维宝典 (二) 文章目录 Kafka运维宝典 (二)一、kafka broker.id冲突问题1. broker.id 冲突的影响2. 如何发现 broker.id 冲突3. 解决 broker.id 冲突的方法4. broker.id 配置管理5. 集群启动后确认 broker.id 唯一性6. brok…...
全球AI模型百科全书,亚马逊云科技Bedrock上的100多款AI模型
今天小李哥给大家介绍的是亚马逊云科技上的AI模型管理平台Amazon Bedrock上的Marketplace,这是亚马逊云科技在今年re:Invent发布的一个全新功能,将亚马逊的电商基因带到了其云计算平台,让我们能够通过Amazon Bedrock访问100多种流行、新兴和专…...
微信小程序中常见的 跳转方式 及其特点的表格总结(wx.navigateTo 适合需要返回上一页的场景)
文章目录 详细说明总结wx.navigateTo 的特点为什么 wx.navigateTo 最常用?其他跳转方式的使用频率总结 以下是微信小程序中常见的跳转方式及其特点的表格总结: 跳转方式API 方法特点适用场景wx.navigateTowx.navigateTo({ url: 路径 })保留当前页面&…...

【Elasticsearch】index:false
在 Elasticsearch 中,index 参数用于控制是否对某个字段建立索引。当设置 index: false 时,意味着该字段不会被编入倒排索引中,因此不能直接用于搜索查询。然而,这并不意味着该字段完全不可访问或没有其他用途。以下是关于 index:…...
新版IDEA创建数据库表
这是老版本的IDEA创建数据库表,下面可以自己勾选Not null(非空),Auto inc(自增长),Unique(唯一标识)和Primary key(主键) 这是新版的IDEA创建数据库表,Not null和Auto inc可以看得到,但Unique和Primary key…...
输入带空格的字符串,求单词个数
输入带空格的字符串,求单词个数 __ueooe_eui_sjje__ ---->3syue__jdjd____die_ ---->3shuue__dju__kk ---->3 #include <stdio.h> #include <string.h>// 自定义函数来判断字符是否为空白字符 int isSpace(char c) {return c || c \t || …...

C语言程序设计十大排序—希尔排序
文章目录 1.概念✅2.希尔排序🎈3.代码实现✅3.1 直接写✨3.2 函数✨ 4.总结✅ 1.概念✅ 排序是数据处理的基本操作之一,每次算法竞赛都很多题目用到排序。排序算法是计算机科学中基础且常用的算法,排序后的数据更易于处理和查找。在计算机发展…...
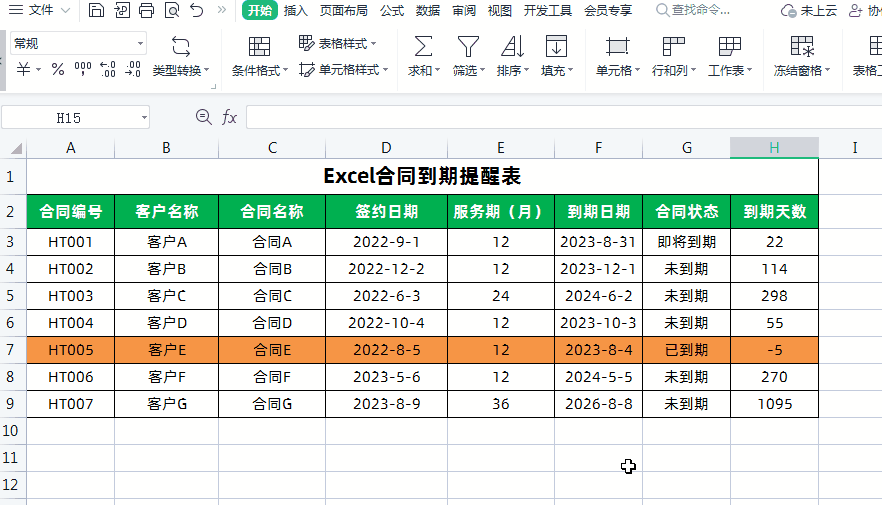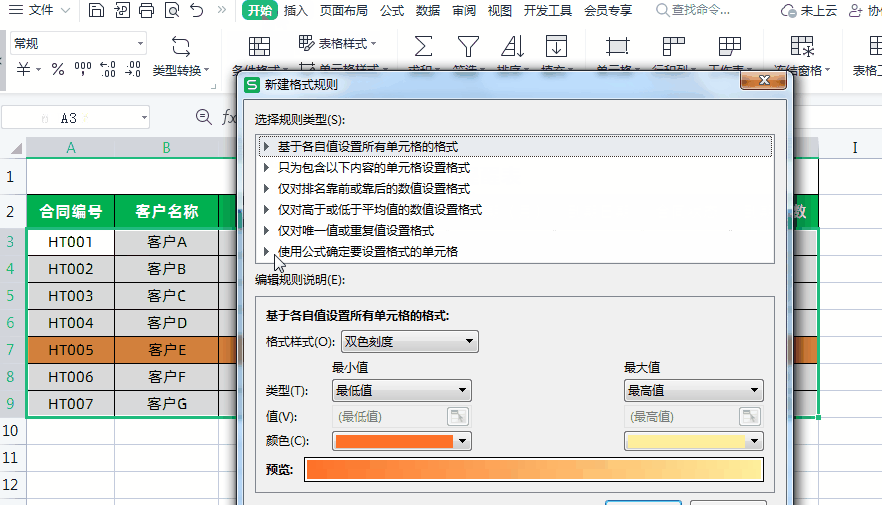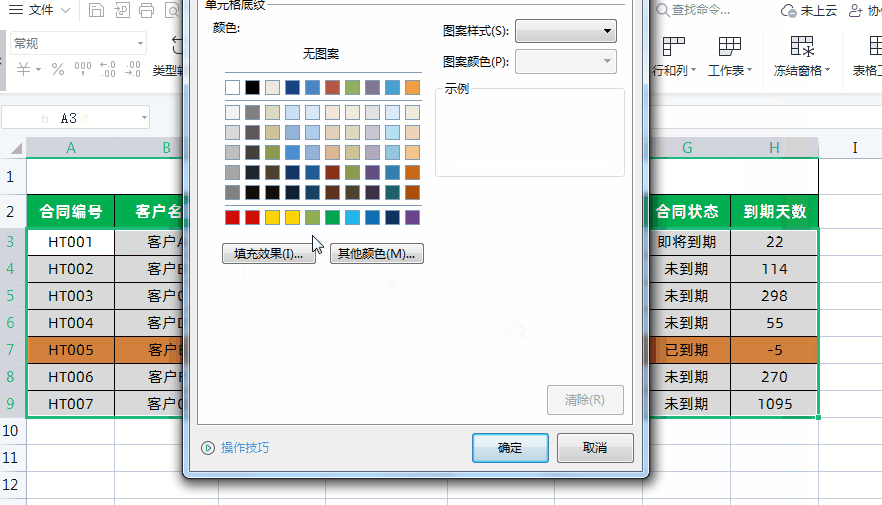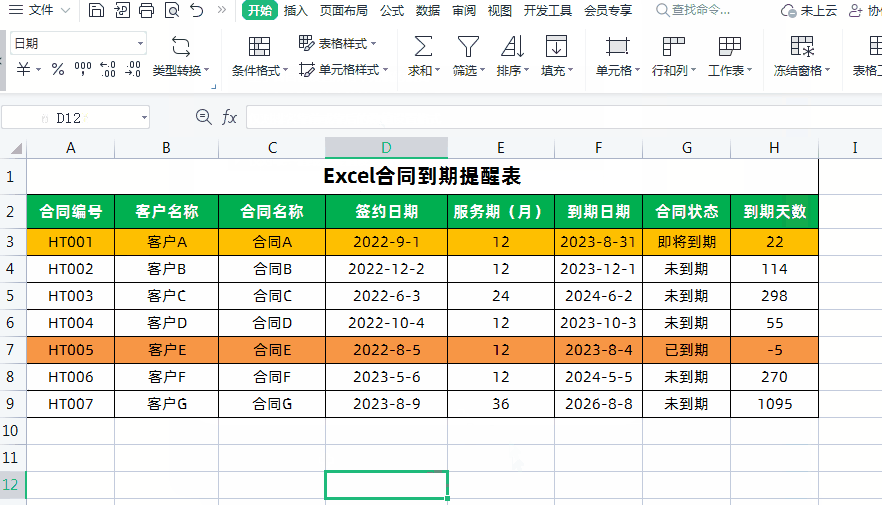
Excel制作合同到期自动提醒!
大家好,我是小鱼。 今天分享一下如何利用Excel制作合同到期提醒表,实现Excel表格自动计算合同到期日和天数,根据合同状态和到期天数自动填充颜色提醒,超实用。先看一下效果,已经到期的合同会自动被填充为红色…...

“AI质量评估系统:智能守护,让品质无忧
嘿,各位小伙伴们!今天咱们来聊聊一个在现代社会中越来越重要的角色——AI质量评估系统。你知道吗?在这个快速发展的时代,产品质量已经成为企业生存和发展的关键。而AI质量评估系统,就像是我们的智能守护神,…...

爬虫基础之爬取某基金网站+数据分析
声明: 本案例仅供学习参考使用,任何不法的活动均与本作者无关 网站:天天基金网(1234567.com.cn) --首批独立基金销售机构-- 东方财富网旗下基金平台! 本案例所需要的模块: 1.requests 2.re(内置) 3.pandas 4.pyecharts 其他均需要 pip install 模块名 爬取步骤: …...

使用 Aryn DocPrep、DocParse 和 Elasticsearch 向量数据库实现高质量 RAG
作者:来自 Elastic Hemant Malik 及 Jonathan Fritz 组织依靠自然语言查询从非结构化数据中获取见解,但要获得高质量的答案,首先要进行有效的数据准备。Aryn DocParse 和 DocPrep通过将复杂文档转换为结构化 JSON 或 markdown 来简化此过程&a…...

Couchbase UI: Server
在 Couchbase UI 中的 Server(服务器)标签页主要用于管理和监控集群中的各个节点。以下是 Server 标签页的主要内容和功能介绍: 1. 节点列表 显示集群中所有节点的列表,每个节点的详细信息包括: 节点地址࿱…...

Web3.0时代的挑战与机遇:以开源2+1链动模式AI智能名片S2B2C商城小程序为例的深度探讨
摘要:Web3.0作为互联网的下一代形态,承载着去中心化、开放性和安全性的重要愿景。然而,其高门槛、用户体验差等问题阻碍了Web3.0的主流化进程。本文旨在深入探讨Web3.0面临的挑战,并提出利用开源21链动模式、AI智能名片及S2B2C商城…...

langchain基础(一)
模型又可分为语言模型(擅长文本补全,输入和输出都是字符串)和聊天模型(擅长对话,输入时消息列表,输出是一个消息)两大类。 以调用openai的聊天模型为例,先安装langchain_openai库 1…...

【Android】布局文件layout.xml文件使用控件属性android:layout_weight使布局较为美观,以RadioButton为例
目录 说明举例 说明 简单来说,android:layout_weight为当前控件按比例分配剩余空间。且单个控件该属性的具体数值不重要,而是多个控件的属性值之比发挥作用,例如有2个控件,各自的android:layout_weight的值设为0.5和0.5࿰…...

RabbitMQ 架构分析
文章目录 前言一、RabbitMQ架构分析1、Broker2、Vhost3、Producer4、Messages5、Connections6、Channel7、Exchange7、Queue8、Consumer 二、消息路由机制1、Direct Exchange2、Topic Exchange3、Fanout Exchange4、Headers Exchange5、notice5.1、备用交换机(Alter…...

Qt Enter和HoverEnter事件
介绍 做PC开发的过程中或多或少都会接触到鼠标的悬停事件,Qt中处理鼠标悬停有Enter和HoverEnter两种事件 相同点 QEvent::Enter对应QEnterEvent,描述的是鼠标进入控件坐标范围之内的行为,QEnterEvent可以抓取鼠标的位置;QEvent…...

大语言模型之prompt工程
前言 随着人工智能的快速发展,我们正慢慢进入AIGC的新时代,其中对自然语言的处理成为了智能化的关键一环,在这个大背景下,“Prompt工程”由此产生,并且正逐渐成为有力的工具... LLM (Large Language Mode…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
