JavaScript逆向高阶指南:突破基础,掌握核心逆向技术
JavaScript逆向高阶指南:突破基础,掌握核心逆向技术
JavaScript逆向工程是Web开发者和安全分析师的核心竞争力。无论是解析混淆代码、分析压缩脚本,还是逆向Web应用架构,掌握高阶逆向技术都将助您深入理解复杂JavaScript逻辑。本文将通过实战案例,带您探索JavaScript逆向的深层技术原理。
1. JavaScript反混淆实战
现代Web应用常采用多重混淆技术保护代码,以下为高效反混淆方法论:
1.1 常见混淆模式识别
- 变量重命名:函数/变量使用
a1B、XyZ等无意义标识 - 字符串编码:采用Base64/十六进制编码或分段存储
- 控制流平坦化:通过冗余条件语句重构执行流程
- 自保护机制:运行时检测调试环境并触发保护
1.2 浏览器开发者工具逆向三板斧
- 代码格式化:使用Chrome DevTools"{}"按钮还原压缩代码
- 断点追踪:在关键执行路径设置断点观察运行时状态
- 动态代码捕获:重载eval函数监控动态执行代码
示例:eval调用拦截
(function() {let originalEval = window.eval;window.eval = function(code) {console.log("捕获动态执行代码:", code);return originalEval(code);};
})();
2. 压缩代码逆向还原
代码压缩通过删除冗余字符和重命名变量实现体积优化,逆向还原技巧包括:
2.1 反压缩工具矩阵
- Beautifier.io:在线代码美化平台
- JSNice:基于AI的变量名智能恢复工具
- UglifyJS:支持语法解析的反压缩利器
2.2 变量名智能还原
当发现a()函数内部调用document.getElementById()时,可将a重命名为getElementByIdWrapper。以下代码可追踪函数调用链:
Function.prototype.call = (function(originalCall) {return function(context, ...args) {console.log("函数调用追踪:", this.name || "匿名函数", "参数列表:", args);return originalCall.apply(this, [context, ...args]);};
})(Function.prototype.call);
3. 隐藏代码挖掘技术
JavaScript常通过动态加载或HTML属性编码实现逻辑隐藏:
3.1 行内事件处理器解析
<button onclick="console.log('隐式验证逻辑')">提交</button>
使用脚本批量提取事件处理器:
document.querySelectorAll("[onclick]").forEach(el => console.log(el.getAttribute("onclick"))
);
3.2 网络请求溯源法
- 开启DevTools网络面板(F12 → Network → XHR/Fetch)
- 筛选.js响应文件并分析内容
- 捕获动态加载的脚本片段
4. 加密代码破解之道
4.1 Base64编码逆向
遇到eval(atob('c29tZV9jb2Rl'))时:
console.log("解码结果:", atob('c29tZV9jb2Rl')); // 输出"some_code"
4.2 XOR加密逆向
常见于安全防护机制,逆向示例:
const encoded = [72, 29, 7];
const key = 42;
const decoded = encoded.map(num => String.fromCharCode(num ^ key));
console.log("解密字符串:", decoded.join('')); // 输出"Hi!"
5. 反调试机制攻防战
5.1 调试阻断绕过
针对debugger;语句的破解方案:
Object.defineProperty(window, 'debugger', {set: () => {},get: () => () => {}
});
5.2 控制台劫持破解
恢复被重写的console方法:
Object.defineProperty(console, 'log', {value: console.__proto__.log
});
技术精要总结
掌握JavaScript逆向工程需要深入理解代码的编写逻辑、混淆机制及运行时特征。通过开发者工具、反混淆技术和定制调试脚本的三重组合,即使面对最复杂的代码结构也能游刃有余。
逆向挑战
解析下列混淆函数的功能并求解返回值:
(function(x){return (x^42).toString(16);})(123)
欢迎在评论区提交你的解答!
本文为您构建了坚实的JavaScript逆向技术体系,无论是安全研究、代码调试还是架构分析,这些高阶技巧都将成为您的神兵利器。如需深入探索JavaScript底层原理,欢迎随时交流探讨!
相关文章:

JavaScript逆向高阶指南:突破基础,掌握核心逆向技术
JavaScript逆向高阶指南:突破基础,掌握核心逆向技术 JavaScript逆向工程是Web开发者和安全分析师的核心竞争力。无论是解析混淆代码、分析压缩脚本,还是逆向Web应用架构,掌握高阶逆向技术都将助您深入理解复杂JavaScript逻辑。本…...

嵌入式知识点总结 Linux驱动 (四)-中断-软硬中断-上下半部-中断响应
针对于嵌入式软件杂乱的知识点总结起来,提供给读者学习复习对下述内容的强化。 目录 1.硬中断,软中断是什么?有什么区别? 2.中断为什么要区分上半部和下半部? 3.中断下半部一般如何实现? 4.linux中断的…...

在ubuntu下一键安装 Open WebUI
该脚本用于自动化安装 Open WebUI,并支持以下功能: 可选跳过 Ollama 安装:通过 --no-ollama 参数跳过 Ollama 的安装。自动清理旧目录:如果安装目录 (~/open-webui) 已存在,脚本会自动删除旧目录并重新安装。完整的依…...

c语言网 1127 尼科彻斯定理
原题 题目描述 验证尼科彻斯定理,即:任何一个整数m的立方都可以写成m个连续奇数之和。 输入格式 任一正整数 输出格式 该数的立方分解为一串连续奇数的和 样例输入 13 样例输出 13*13*132197157159161163165167169171173175177179181 #include<ios…...
Cloudflare通过代理服务器绕过 CORS 限制:原理、实现场景解析
第一部分:问题背景 1.1 错误现象复现 // 浏览器控制台报错示例 Access to fetch at https://chat.qwenlm.ai/api/v1/files/ from origin https://ocr.doublefenzhuan.me has been blocked by CORS policy: Response to preflight request doesnt pass access con…...
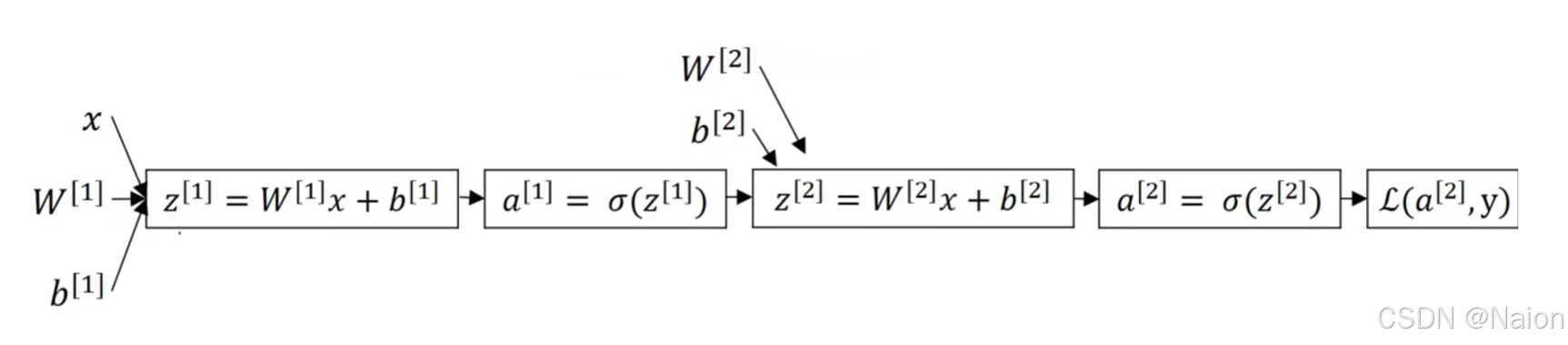
吴恩达深度学习——如何实现神经网络
来自吴恩达深度学习,仅为本人学习所用。 文章目录 神经网络的表示计算神经网络的输出激活函数tanh选择激活函数为什么需要非激活函数双层神经网络的梯度下降法 随机初始化 神经网络的表示 对于简单的Logistic回归,使用如下的计算图。 如果是多个神经元…...

《STL基础之vector、list、deque》
【vector、list、deque导读】vector、list、deque这三种序列式的容器,算是比较的基础容器,也是大家在日常开发中常用到的容器,因为底层用到的数据结构比较简单,笔者就将他们三者放到一起做下对比分析,介绍下基本用法&a…...

LockSupport概述、阻塞方法park、唤醒方法unpark(thread)、解决的痛点、带来的面试题
目录 ①. 什么是LockSupport? ②. 阻塞方法 ③. 唤醒方法(注意这个permit最多只能为1) ④. LockSupport它的解决的痛点 ⑤. LockSupport 面试题目 ①. 什么是LockSupport? ①. 通过park()和unpark(thread)方法来实现阻塞和唤醒线程的操作 ②. LockSupport是一个线程阻塞…...
Android开发基础知识
1 什么是Android? Android(读音:英:[ndrɔɪd],美:[ˈnˌdrɔɪd]),常见的非官方中文名称为安卓,是一个基于Linux内核的开放源代码移动操作系统,由Google成立…...

C++ Lambda 表达式的本质及原理分析
目录 1.引言 2.Lambda 的本质 3.Lambda 的捕获机制的本质 4.捕获方式的实现与底层原理 5.默认捕获的实现原理 6.捕获 this 的机制 7.捕获的限制与注意事项 8.总结 1.引言 C 中的 Lambda 表达式是一种匿名函数,最早在 C11 引入,用于简化函数对象的…...
《多线程基础之条件变量》
【条件变量导读】条件变量是多线程中比较灵活而且容易出错的线程同步手段,比如:虚假唤醒、为啥条件变量要和互斥锁结合使用?windows和linux双平台下,初始化、等待条件变量的api一样吗? 本文将分别为您介绍条件变量在w…...
21款炫酷烟花合集
系列专栏 《Python趣味编程》《C/C趣味编程》《HTML趣味编程》《Java趣味编程》 写在前面 Python、C/C、HTML、Java等4种语言实现18款炫酷烟花的代码。 Python Python烟花① 完整代码:Python动漫烟花(完整代码) Python烟花② 完整…...

智能风控 数据分析 groupby、apply、reset_index组合拳
目录 groupby——分组 本例 apply——对每个分组应用一个函数 等价用法 reset_index——重置索引 使用前编辑 注意事项 groupby必须配合聚合函数、 关于agglist 一些groupby试验 1. groupby对象之后。sum(一个列名) 2. groupby对象…...

Python网络自动化运维---用户交互模块
文章目录 目录 文章目录 前言 实验环境准备 一.input函数 代码分段解析 二.getpass模块 前言 在前面的SSH模块章节中,我们都是将提供SSH服务的设备的账户/密码直接写入到python代码中,这样很容易导致账户/密码泄露,而使用Python中的用户交…...

【JVM】调优
目的: 减少minor gc、full gc的次数,也就是减少STW的时间,因为java虚拟机在做后台垃圾收集线程的时候,会停掉其他线程,专门做垃圾收集,这样会影响网站的性能,以及用户的体验。 调优位置&#x…...
软件测试 —— jmeter(2)
软件测试 —— jmeter(2) HTTP默认请求头(元件)元件作用域和取样器作用域HTTP Cookie管理器同步定时器jmeter插件梯度压测线程组(Stepping Thread Group)参数解析总结 Response Times over TimeActive Thre…...
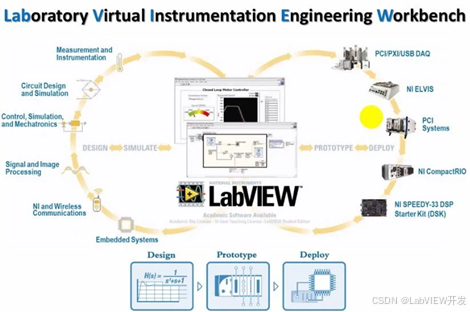
为什么LabVIEW适合软硬件结合的项目?
LabVIEW是一种基于图形化编程的开发平台,广泛应用于软硬件结合的项目中。其强大的硬件接口支持、实时数据采集能力、并行处理能力和直观的用户界面,使得它成为工业控制、仪器仪表、自动化测试等领域中软硬件系统集成的理想选择。LabVIEW的设计哲学强调模…...

【机器学习】自定义数据集 使用tensorflow框架实现逻辑回归并保存模型,然后保存模型后再加载模型进行预测
一、使用tensorflow框架实现逻辑回归 1. 数据部分: 首先自定义了一个简单的数据集,特征 X 是 100 个随机样本,每个样本一个特征,目标值 y 基于线性关系并添加了噪声。tensorflow框架不需要numpy 数组转换为相应的张量࿰…...

.NET Core缓存
目录 缓存的概念 客户端响应缓存 cache-control 服务器端响应缓存 内存缓存(In-memory cache) 用法 GetOrCreateAsync 缓存过期时间策略 缓存的过期时间 解决方法: 两种过期时间策略: 绝对过期时间 滑动过期时间 两…...
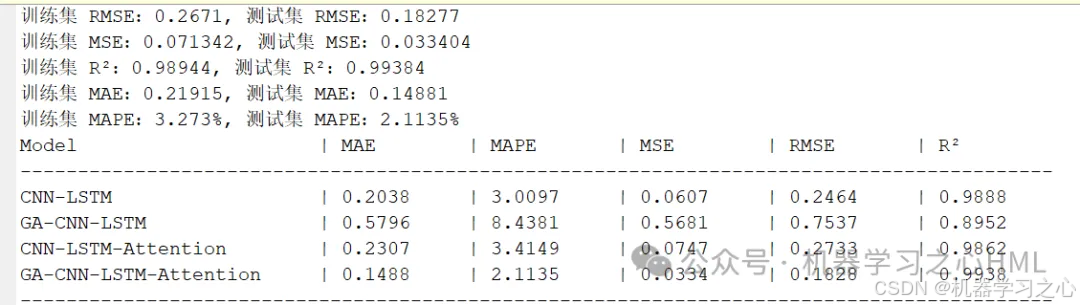
GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比
GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比 目录 GA-CNN-LSTM-Attention、CNN-LSTM-Attention、GA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比预测效果基本介绍程序设计参考资料 预测效果 基本介绍 基于GA-CNN-LST…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
