C++进阶课程第2期——排列与组合1
大家好,我是清墨,欢迎收看《C++进阶课程——排列与组合》。

啊,上一期我们的情况啊也是非常好的,今天直接开始!
排列(Arrange)
与上期一样啊,我们先了解一下排列的概念。
排列是指将一组事物按照一定的顺序进行摆放的方式。在数学中,排列是指从一组事物中选取若干个进行组合,并按照特定的顺序进行排列的方法。
至于怎样表示呢就用表示从n个元素中选择m个元素进行排列,所有的方案数。
是n的全排列,结果是n的阶乘(n!)。
计算: =
。
组合(Combination)
组合是从给定的元素集合中选取一些元素的方式。在组合中,选取的元素的顺序是不重要的,也就是说,(1,2,3)和(3,2,1)被视为相同的组合。
至于怎样表示呢就用表示从n个元素中选择m个元素进行组合,所有的方案数。
计算: =
海题——杨辉三角
题目描述
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
上面的图形熟悉吗?如果还没看出来它的特点的话,不妨再调整一下格式:
11 11 2 11 3 3 11 4 6 4 1
1 5 10 10 5 1
是不是看出这些数字的特点了?这是大名鼎鼎的杨辉三角。
今天,我们试着来输出 n 行的杨辉三角数字。
输入格式 1 个正整数:n。
输出格式 相应层数的杨辉三角数字。
样例
输入数据 1
6
输出数据 1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[111][111];
int main(){cin>>n;a[1][1]=1;a[2][1]=1;a[2][2]=1;for(int i=3;i<=n;i++){for(int j=1;j<=n;j++){a[i][j]=a[i-1][j]+a[i-1][j-1];}}for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cout<<a[i][j]<<" ";}cout<<endl;}return 0;
}杨辉三角有什么用呢,先买个管子,进入例题。
例题1.派水果
题目描述
若一位母亲手里有 m 个相同的苹果,还有 n 个相同的梨,在 m+n 天内分给她的小孩,每天分 1 个水果,有多少种不同的分派方案?。
输入格式 两个整数 m 和 n ( 1≤m,n≤32)。
输出格式 一个整数。结果不超出 max long long
样例
输入数据 1
2 3
输出数据 1
10分析题目
本题确定了苹果的位置就可以确定梨的位置,又因为苹果和梨都相同,所以不用考虑顺序。
只用求 或
就可以了。
所以=
。
但是,直接计算必须会超,在我们计算32的阶乘时,就会溢出。

“e+35”!10的35次方,超出了long long范围,那要怎样计算呢?
找规律
我们不妨试试小点的C。
用原本的代码计算小一点的。
#include<bits/stdc++.h>
using namespace std;
long long ans1=1,ans2=1,n,m;
int main(){cin>>n>>m;n+=m;for(long long i=n;i>=n-m+1;i--){ans1*=i;}for(long long i=m;i>=1;i--){ans2*=i;}cout<<ans1/ans2;return 0;
}得 :
=1
=1
=2
=1
=3
=3
=1
=4
=6
=4
=1
有点感觉了吗?
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
杨辉三角!
代码
写得代码
#include<bits/stdc++.h>
using namespace std;
long long n,a[11100][11000],m;
int main(){cin>>n>>m;n+=m;a[1][1]=1;a[1][2]=1;for(int i=2;i<=n;i++){for(int j=1;j<=n;j++){a[i][j]=a[i-1][j]+a[i-1][j-1];}}cout<<a[n][n-m+1];return 0;
}所以杨辉三角可不只是数学游戏和海题,在实际应用中有大用。例如在计算组合方案数的时候,C(n, m) = C(n-1,m) + C(n-1, m-1),从而避免了组合公式中的除法运算(除法运算的计算机代码要复杂很多,远远没有加法容易处理)。
我们下期再见。

相关文章:

C++进阶课程第2期——排列与组合1
大家好,我是清墨,欢迎收看《C进阶课程——排列与组合》。 啊,上一期我们的情况啊也是非常好的,今天直接开始! 排列(Arrange) 与上期一样啊,我们先了解一下排列的概念。 排列是指将…...

C++17 std::variant 详解:概念、用法和实现细节
文章目录 简介基本概念定义和使用std::variant与传统联合体union的区别 多类型值存储示例初始化修改判断variant中对应类型是否有值获取std::variant中的值获取当前使用的type在variant声明中的索引 访问std::variant中的值使用std::get使用std::get_if 错误处理和访问未初始化…...

Leetcode::119. 杨辉三角 II
119. 杨辉三角 II 已解答 简单 相关标签 相关企业 给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。 在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例 1: 输入: rowIndex 3 输出: [1,3,3,1]示例 2: 输入: rowIndex 0…...

多模态论文笔记——TECO
大家好,这里是好评笔记,公主号:Goodnote,专栏文章私信限时Free。本文详细解读多模态论文TECO(Temporally Consistent Transformer),即时间一致变换器,是一种用于视频生成的创新模型&…...

Ubuntu 16.04用APT安装MySQL
个人博客地址:Ubuntu 16.04用APT安装MySQL | 一张假钞的真实世界 安装MySQL 用以下命令安装MySQL: sudo apt-get install mysql-server 这个命令会安装MySQL服务器、客户端和公共文件。安装过程会出现两个要求输入的对话框: 输入MySQL root用户的密…...

Linux 4.19内核中的内存管理:x86_64架构下的实现与源码解析
在现代操作系统中,内存管理是核心功能之一,它直接影响系统的性能、稳定性和多任务处理能力。Linux 内核在 x86_64 架构下,通过复杂的机制实现了高效的内存管理,涵盖了虚拟内存、分页机制、内存分配、内存映射、内存保护、缓存管理等多个方面。本文将深入探讨这些机制,并结…...

JavaScript逆向高阶指南:突破基础,掌握核心逆向技术
JavaScript逆向高阶指南:突破基础,掌握核心逆向技术 JavaScript逆向工程是Web开发者和安全分析师的核心竞争力。无论是解析混淆代码、分析压缩脚本,还是逆向Web应用架构,掌握高阶逆向技术都将助您深入理解复杂JavaScript逻辑。本…...

嵌入式知识点总结 Linux驱动 (四)-中断-软硬中断-上下半部-中断响应
针对于嵌入式软件杂乱的知识点总结起来,提供给读者学习复习对下述内容的强化。 目录 1.硬中断,软中断是什么?有什么区别? 2.中断为什么要区分上半部和下半部? 3.中断下半部一般如何实现? 4.linux中断的…...

在ubuntu下一键安装 Open WebUI
该脚本用于自动化安装 Open WebUI,并支持以下功能: 可选跳过 Ollama 安装:通过 --no-ollama 参数跳过 Ollama 的安装。自动清理旧目录:如果安装目录 (~/open-webui) 已存在,脚本会自动删除旧目录并重新安装。完整的依…...

c语言网 1127 尼科彻斯定理
原题 题目描述 验证尼科彻斯定理,即:任何一个整数m的立方都可以写成m个连续奇数之和。 输入格式 任一正整数 输出格式 该数的立方分解为一串连续奇数的和 样例输入 13 样例输出 13*13*132197157159161163165167169171173175177179181 #include<ios…...
Cloudflare通过代理服务器绕过 CORS 限制:原理、实现场景解析
第一部分:问题背景 1.1 错误现象复现 // 浏览器控制台报错示例 Access to fetch at https://chat.qwenlm.ai/api/v1/files/ from origin https://ocr.doublefenzhuan.me has been blocked by CORS policy: Response to preflight request doesnt pass access con…...
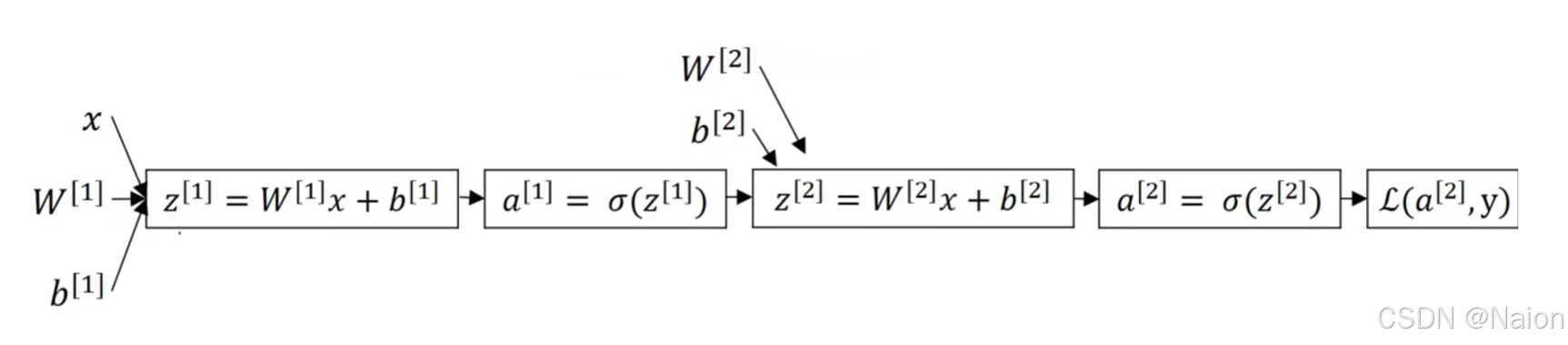
吴恩达深度学习——如何实现神经网络
来自吴恩达深度学习,仅为本人学习所用。 文章目录 神经网络的表示计算神经网络的输出激活函数tanh选择激活函数为什么需要非激活函数双层神经网络的梯度下降法 随机初始化 神经网络的表示 对于简单的Logistic回归,使用如下的计算图。 如果是多个神经元…...

《STL基础之vector、list、deque》
【vector、list、deque导读】vector、list、deque这三种序列式的容器,算是比较的基础容器,也是大家在日常开发中常用到的容器,因为底层用到的数据结构比较简单,笔者就将他们三者放到一起做下对比分析,介绍下基本用法&a…...

LockSupport概述、阻塞方法park、唤醒方法unpark(thread)、解决的痛点、带来的面试题
目录 ①. 什么是LockSupport? ②. 阻塞方法 ③. 唤醒方法(注意这个permit最多只能为1) ④. LockSupport它的解决的痛点 ⑤. LockSupport 面试题目 ①. 什么是LockSupport? ①. 通过park()和unpark(thread)方法来实现阻塞和唤醒线程的操作 ②. LockSupport是一个线程阻塞…...
Android开发基础知识
1 什么是Android? Android(读音:英:[ndrɔɪd],美:[ˈnˌdrɔɪd]),常见的非官方中文名称为安卓,是一个基于Linux内核的开放源代码移动操作系统,由Google成立…...

C++ Lambda 表达式的本质及原理分析
目录 1.引言 2.Lambda 的本质 3.Lambda 的捕获机制的本质 4.捕获方式的实现与底层原理 5.默认捕获的实现原理 6.捕获 this 的机制 7.捕获的限制与注意事项 8.总结 1.引言 C 中的 Lambda 表达式是一种匿名函数,最早在 C11 引入,用于简化函数对象的…...
《多线程基础之条件变量》
【条件变量导读】条件变量是多线程中比较灵活而且容易出错的线程同步手段,比如:虚假唤醒、为啥条件变量要和互斥锁结合使用?windows和linux双平台下,初始化、等待条件变量的api一样吗? 本文将分别为您介绍条件变量在w…...
21款炫酷烟花合集
系列专栏 《Python趣味编程》《C/C趣味编程》《HTML趣味编程》《Java趣味编程》 写在前面 Python、C/C、HTML、Java等4种语言实现18款炫酷烟花的代码。 Python Python烟花① 完整代码:Python动漫烟花(完整代码) Python烟花② 完整…...

智能风控 数据分析 groupby、apply、reset_index组合拳
目录 groupby——分组 本例 apply——对每个分组应用一个函数 等价用法 reset_index——重置索引 使用前编辑 注意事项 groupby必须配合聚合函数、 关于agglist 一些groupby试验 1. groupby对象之后。sum(一个列名) 2. groupby对象…...

Python网络自动化运维---用户交互模块
文章目录 目录 文章目录 前言 实验环境准备 一.input函数 代码分段解析 二.getpass模块 前言 在前面的SSH模块章节中,我们都是将提供SSH服务的设备的账户/密码直接写入到python代码中,这样很容易导致账户/密码泄露,而使用Python中的用户交…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
