动态规划DP 最长上升子序列模型 合唱队形(题目分析+C++完整代码)
概览检索
动态规划DP 最长上升子序列模型
合唱队形
原题链接
AcWiing 482. 合唱队形
题目描述
N位同学站成一排,音乐老师要请其中的 (N−K)位同学出列,使得剩下的 K位同学排成合唱队形。
合唱队形是指这样的一种队形:设 K位同学从左到右依次编号为 1,2…,K,他们的身高分别为 T1,T2,…,TK,
则他们的身高满足 T1<…Ti+1>…>TK(1≤i≤K)。
你的任务是,已知所有 N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
输入格式
输入的第一行是一个整数 N,表示同学的总数。
第二行有 N个整数,用空格分隔,第 i个整数 Ti是第 i 位同学的身高(厘米)。
输出格式
输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。
数据范围
2≤N≤100,130≤Ti≤230
输入样例:
8
186 186 150 200 160 130 197 220
输出样例:
4
题目分析
由合唱队形满足的要求 身高满足 T1<…Ti+1>…>TK 可知该队形就是一个先上升后下降的子序列;
最少去掉的同学 即使合唱队形中的人数最多。
由此联想到 登山(点击链接跳转题目)。
也可参考 怪盗基德的滑翔伞(点击链接跳转题目)。
以最高的同学为划分,划分为左半部分的递增子序列,和右半部分的递减子序列(也就是相当于逆着的递增子序列),可直接看出该题为最长上升子序列模型。
分别求出左半部分和右半部分在以不同同学为那个顶峰时的值,分别存储在 f[i], g[i] 中。
则对应一个顶峰同学为i的合唱队形下的人数为 f[i]+g[i]-1 ,
遍历所有1~n的可能情形下,取其中人数最多(数值最大)的值max,
则出列的最少同学的数目为总人数n 减去该最大值max。
完整代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N=110;
int n;
int a[N],f[N],g[N];
int main(){scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);//左半部分递增子序列for(int i=1;i<=n;i++){f[i]=1; //序列中只有a[i],长度为1//前一个数为a[j]for(int j=1;j<i;j++)if(a[j]<a[i]) //满足前一个数a[j]大于后一个数a[i]f[i]=max(f[i],f[j]+1); //尝试更新,f[j]+1为以前一个数a[j]结尾的最长序列的长度f[j]再加上当前最有一个数a[i](长度为1)}//右半部分递减子序列for(int i=n;i>=1;i--){g[i]=1;for(int j=n;j>i;j--)if(a[j]<a[i])g[i]=max(g[i],g[j]+1);}int res=0;for(int i=1;i<=n;i++) res=max(res,f[i]+g[i]-1); //取和的最大值printf("%d",n-res); //所有人数-最大值return 0;
}
相关文章:
)
动态规划DP 最长上升子序列模型 合唱队形(题目分析+C++完整代码)
概览检索 动态规划DP 最长上升子序列模型 合唱队形 原题链接 AcWiing 482. 合唱队形 题目描述 N位同学站成一排,音乐老师要请其中的 (N−K)位同学出列,使得剩下的 K位同学排成合唱队形。 合唱队形是指这样的一种队形:设 K位同学从左到右…...

【踩坑】解决Hugging-face下载问题
解决Hugging-face下载问题 问题1:couldnt connect to https://huggingface.co问题2:HTTPSConnectionPool(hostcdn-lfs-us-1.hf-mirror.com, port443)设置hf_transfer加快速度 问题3:requests.exceptions.ChunkedEncodingError: (Connection b…...

Spring AI 在微服务中的应用:支持分布式 AI 推理
1. 引言 在现代企业中,微服务架构 已成为开发复杂系统的主流方式,而 AI 模型推理 也越来越多地被集成到业务流程中。如何在分布式微服务架构下高效地集成 Spring AI,使多个服务可以协同完成 AI 任务,并支持分布式 AI 推理&#x…...

5.3.2 软件设计原则
文章目录 抽象模块化信息隐蔽与独立性衡量 软件设计原则:抽象、模块化、信息隐蔽。 抽象 抽象是抽出事物本质的共同特性。过程抽象是指将一个明确定义功能的操作当作单个实体看待。数据抽象是对数据的类型、操作、取值范围进行定义,然后通过这些操作对数…...

java求职学习day20
1 在线考试系统 1.1 软件开发的流程 需求分析文档、概要设计文档、详细设计文档、编码和测试、安装和调试、维护和升级 1.2 软件的需求分析 在线考试系统的主要功能分析如下: ( 1 )学员系统 (1.1)用户模块&…...

Python NumPy(8):NumPy 位运算、NumPy 字符串函数
1 NumPy 位运算 位运算是一种在二进制数字的位级别上进行操作的一类运算,它们直接操作二进制数字的各个位,而不考虑数字的整体值。NumPy 提供了一系列位运算函数,允许对数组中的元素进行逐位操作,这些操作与 Python 的位运算符类似…...

日志2025.1.30
日志2025.1.30 1.简略地做了一下交互系统 public class Interactable : MonoBehaviour { private MeshRenderer renderer; private Material defaultMaterial; public Material highlightMaterial; private void Awake() { renderer GetComponentInChildren<Me…...

实战:如何快速让新网站被百度收录?
本文来自:百万收录网 原文链接:https://www.baiwanshoulu.com/22.html 要让新网站快速被百度收录,可以采取以下实战策略: 一、网站基础优化 网站结构清晰:确保网站的结构简洁清晰,符合百度的抓取规则。主…...

PhotoShop中JSX编辑器安装
1.使用ExtendScript Tookit CC编辑 1.安装 打开CEP Resource链接: CEP-Resources/ExtendScript-Toolkit at master Adobe-CEP/CEP-Resources (github.com) 将文件clone到本地或者下载到本地 点击AdobeExtendScriptToolKit_4_Ls22.exe安装,根据弹出的…...

01-时间与管理
时间与效率 一丶番茄时钟步骤好处 二丶86400s的财富利用时间的方法每天坚持写下一天计划 自我管理体系计划-行动-评价-回顾 一丶番茄时钟 一个计时器 一份任务清单,任务 步骤 每一个25分钟是一个番茄时钟 将工作时间划分为若干个25分钟的工作单元期间只专注于当前任务,遇到…...

MiniMax-01技术报告解读
刚刚MiniMax发布了MiniMax-01,简单测试了效果,感觉不错。于是又把它的技术报告看了一下。这种报告看多了,就会多一个毛病,越来越觉得自己也能搞一个。 这篇文章我觉得最有意思的一句是对数据质量的强调“低质量数据在训练超过两个…...
:让大模型“轻装上阵”的技术革新——从DeepSeek看下一代语言模型的高效之路)
多头潜在注意力(MLA):让大模型“轻装上阵”的技术革新——从DeepSeek看下一代语言模型的高效之路
多头潜在注意力(MLA):让大模型“轻装上阵”的技术革新 ——从DeepSeek看下一代语言模型的高效之路 大模型的“内存焦虑” 当ChatGPT等大语言模型(LLM)惊艳世界时,很少有人意识到它们背后隐藏的“内存焦虑”…...

哈希表实现
目录 1. 哈希概念 1.1 直接定址法 1.2 哈希冲突 1.3 负载因子 1.4 将关键字转为整型 1.5 哈希函数 1.5.1 除法散列法/除留余数法 1.5.2 乘法散列法 1.5.3 全域散列法 1.5.4 其他方法 1.6 处理哈希冲突 1.6.1 开放定址法 1.6.1.1 线性探测 1.6.1.2 二次探测 1.6.…...
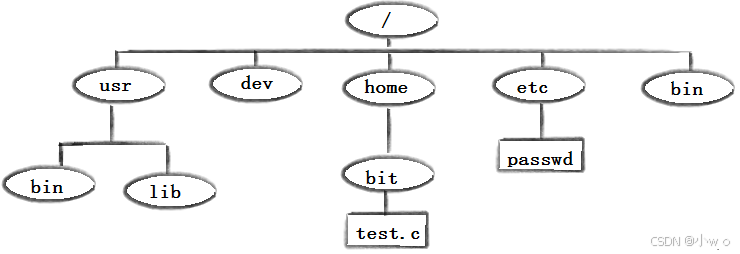
Linux的常用指令的用法
目录 Linux下基本指令 whoami ls指令: 文件: touch clear pwd cd mkdir rmdir指令 && rm 指令 man指令 cp mv cat more less head tail 管道和重定向 1. 重定向(Redirection) 2. 管道(Pipes&a…...

Ubuntu安装VMware17
安装 下载本文的附件,之后执行 sudo chmod x VMware-Workstation-Full-17.5.2-23775571.x86_64.bundle sudo ./VMware-Workstation-Full-17.5.2-23775571.x86_64.bundle安装注意事项: 跳过账户登录的办法:断开网络 可能出现的问题以及解决…...
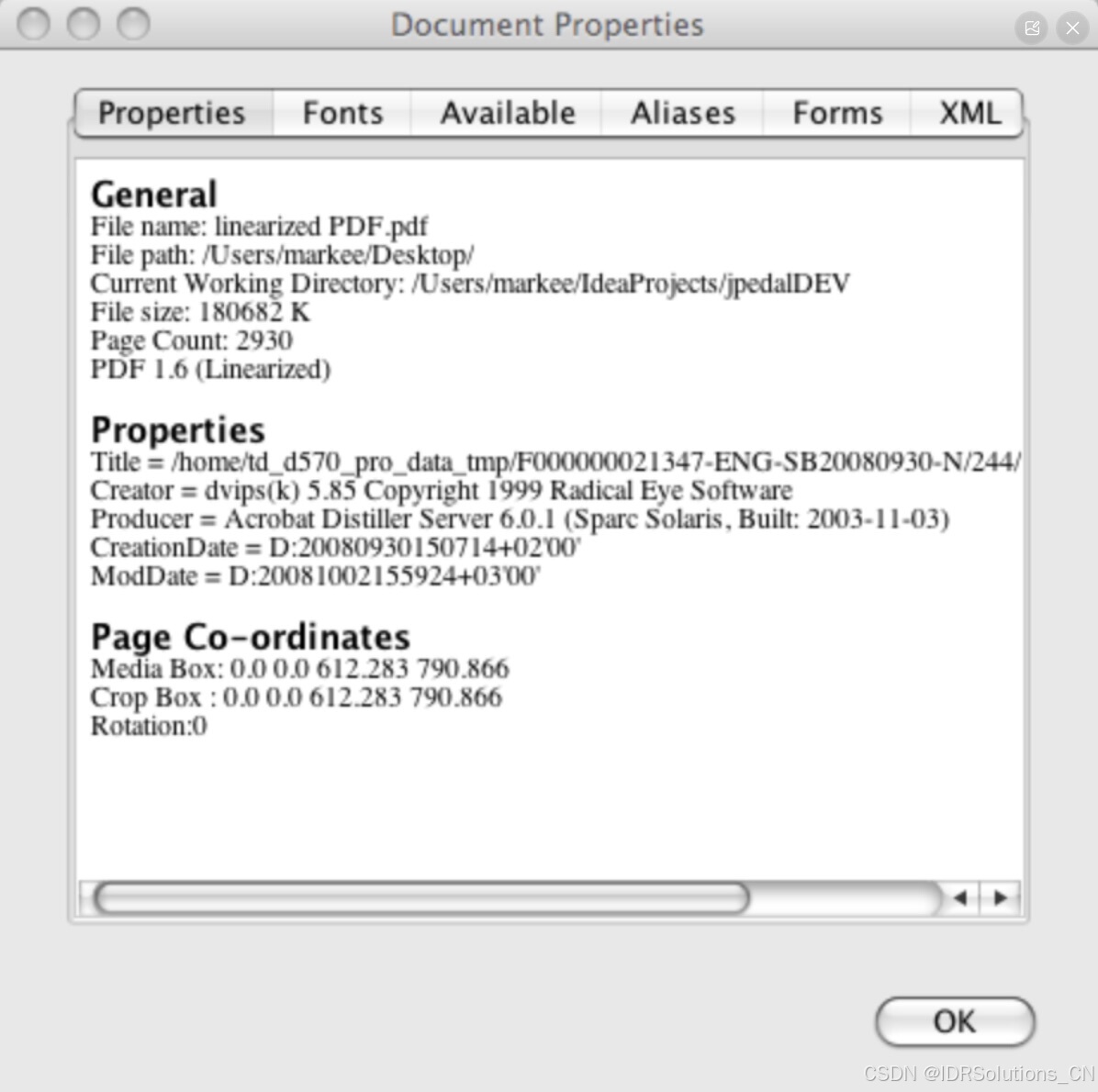
什么是线性化PDF?
线性化PDF是一种特殊的PDF文件组织方式。 总体而言,PDF是一种极为优雅且设计精良的格式。PDF由大量PDF对象构成,这些对象用于创建页面。相关信息存储在一棵二叉树中,该二叉树同时记录文件中每个对象的位置。因此,打开文件时只需加…...
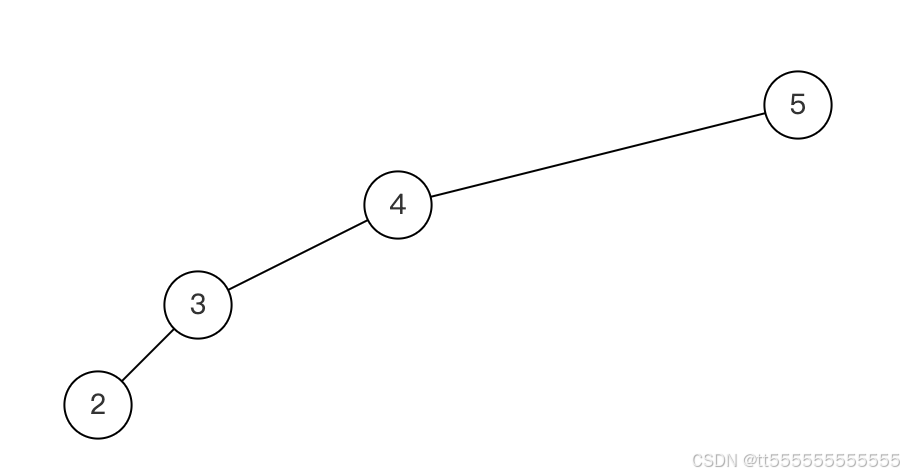
每日一题——序列化二叉树
序列化二叉树 BM39 序列化二叉树题目描述序列化反序列化 示例示例1示例2 解题思路序列化过程反序列化过程 代码实现代码说明复杂度分析总结 BM39 序列化二叉树 题目描述 请实现两个函数,分别用来序列化和反序列化二叉树。二叉树的序列化是将二叉树按照某种遍历方式…...
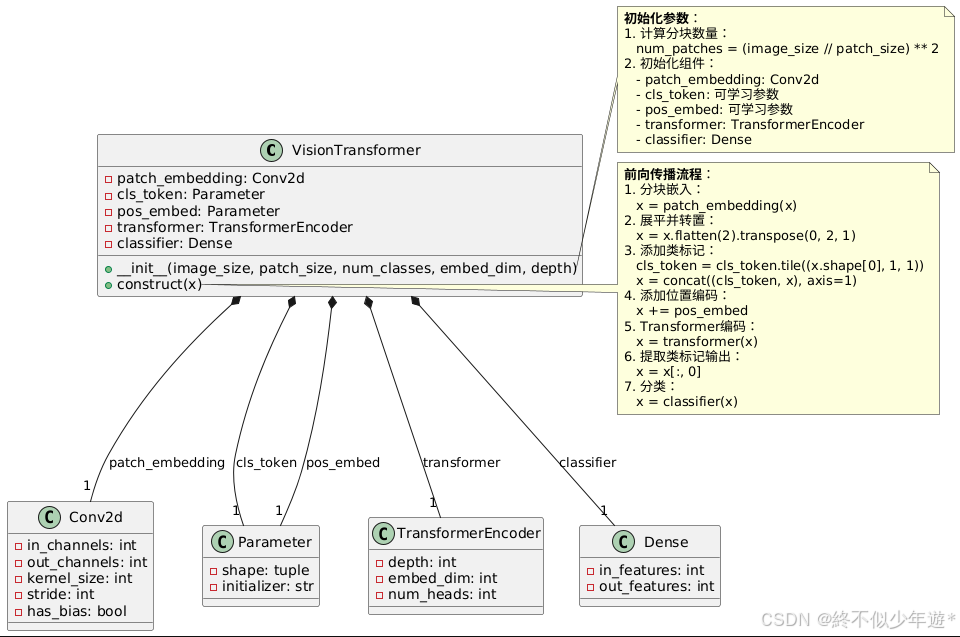
Transformer+vit原理分析
目录 一、Transformer的核心思想 1. 自注意力机制(Self-Attention) 2. 多头注意力(Multi-Head Attention) 二、Transformer的架构 1. 整体结构 2. 编码器层(Encoder Layer) 3. 解码器层(Decoder…...
「AI学习笔记」深度学习的起源与发展:从神经网络到大数据(二)
深度学习(DL)是现代人工智能(AI)的核心之一,但它并不是一夜之间出现的技术。从最初的理论提出到如今的广泛应用,深度学习经历了几乎一个世纪的不断探索与发展。今天,我们一起回顾深度学习的历史…...
【漫话机器学习系列】069.哈达马乘积(Hadamard Product)
哈达马乘积(Hadamard Product) 哈达马乘积(Hadamard Product)是两个矩阵之间的一种元素级操作,也称为逐元素乘积(Element-wise Product)。它以矩阵的对应元素相乘为规则,生成一个新…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
