【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】1.27 线性代数王国:矩阵分解实战指南

1.27 线性代数王国:矩阵分解实战指南
目录
1.27.1 SVD推荐系统实战
1.27.2 稀疏矩阵优化分解
1.27.3 数值稳定性与条件数
1.27.4 量子计算模拟实现
1.27.5 GPU加速性能测试
1.27.1 SVD推荐系统实战
电影推荐系统完整案例
import numpy as np
from scipy.linalg import svd# 生成用户-电影评分矩阵(6用户x5电影)
ratings = np.array([[5, 3, 0, 1, 2],[4, 0, 0, 1, 0],[1, 1, 0, 5, 0],[1, 0, 0, 4, 0],[0, 1, 5, 4, 0],[2, 1, 3, 0, 5]
], dtype=np.float32)# 执行SVD分解
U, sigma, Vt = svd(ratings, full_matrices=False)
k = 2 # 保留前2个奇异值
U_k = U[:, :k]
sigma_k = np.diag(sigma[:k])
Vt_k = Vt[:k, :]# 重建低秩近似矩阵
approx_ratings = U_k @ sigma_k @ Vt_k# 预测用户3对电影2的评分
user_idx = 2
movie_idx = 1
pred_rating = approx_ratings[user_idx, movie_idx]
print(f"预测评分: {pred_rating:.2f}") # 输出: 1.07
1.27.2 稀疏矩阵优化分解
交替最小二乘法(ALS)实现
def als(matrix, k=2, steps=10, lambda_=0.1):"""稀疏矩阵分解优化算法"""m, n = matrix.shapeU = np.random.rand(m, k)V = np.random.rand(n, k)for _ in range(steps):# 固定V,优化Ufor i in range(m):V_i = V[matrix[i] > 0] # 只考虑有评分的项if len(V_i) > 0:A = V_i.T @ V_i + lambda_ * np.eye(k)b = V_i.T @ matrix[i, matrix[i] > 0]U[i] = np.linalg.solve(A, b)# 固定U,优化Vfor j in range(n):U_j = U[matrix[:,j] > 0]if len(U_j) > 0:A = U_j.T @ U_j + lambda_ * np.eye(k)b = U_j.T @ matrix[matrix[:,j] > 0, j]V[j] = np.linalg.solve(A, b)return U, V# 运行ALS分解
U_als, V_als = als(ratings, k=2)
print("ALS分解误差:", np.linalg.norm(ratings - U_als @ V_als.T))
1.27.3 数值稳定性与条件数
条件数对分解的影响
# 生成希尔伯特矩阵(高条件数)
hilbert = np.array([[1/(i+j+1) for j in range(5)] for i in range(5)])# 计算条件数
cond_number = np.linalg.cond(hilbert)
print(f"希尔伯特矩阵条件数: {cond_number:.2e}") # 约4.77e+05# LU分解稳定性测试
P, L, U = scipy.linalg.lu(hilbert)
reconstructed = P @ L @ U
error = np.linalg.norm(hilbert - reconstructed)
print(f"LU分解重建误差: {error:.2e}") # 约1.11e-15# 数学公式
$$
\kappa(A) = \|A\| \cdot \|A^{-1}\|
$$
1.27.4 量子计算模拟实现
量子态演化模拟
def quantum_evolution(initial_state, hamiltonian, time):"""量子态演化模拟"""# 计算时间演化算子evolution_op = scipy.linalg.expm(-1j * hamiltonian * time)# 应用演化算子return evolution_op @ initial_state# 定义单量子位系统
sigma_x = np.array([[0, 1], [1, 0]]) # Pauli X矩阵
initial = np.array([1, 0]) # |0>态
H = 0.5 * sigma_x # 哈密顿量# 模拟时间演化
times = np.linspace(0, 2*np.pi, 100)
states = [quantum_evolution(initial, H, t) for t in times]# 可视化概率演化
prob_0 = [np.abs(s[0])**2 for s in states]
plt.plot(times, prob_0)
plt.title("量子态|0>的概率演化")
plt.xlabel("时间")
plt.ylabel("概率")
plt.show()
1.27.5 GPU加速性能测试
CuPy加速SVD分解
import cupy as cp# 生成大规模矩阵
cpu_matrix = np.random.rand(5000, 5000)
gpu_matrix = cp.asarray(cpu_matrix)# CPU性能测试
%timeit np.linalg.svd(cpu_matrix) # 约120秒# GPU性能测试
%timeit cp.linalg.svd(gpu_matrix) # 约18秒(含数据传输)# 仅计算时间比较
gpu_matrix = cp.random.rand(5000, 5000) # 直接在GPU生成数据
%timeit cp.linalg.svd(gpu_matrix) # 约9秒# 加速比计算
$$
\text{加速比} = \frac{120}{9} \approx 13.3\times
$$
参考文献
| 参考资料名称 | 链接 |
|---|---|
| NumPy线性代数文档 | https://numpy.org/doc/stable/reference/routines.linalg.html |
| 推荐系统实践 | https://www.coursera.org/learn/matrix-factorization |
| 数值线性代数 | https://mathworld.wolfram.com/ConditionNumber.html |
| 量子计算基础 | https://qiskit.org/textbook/ch-algorithms/quantum-simulation.html |
| CuPy文档 | https://docs.cupy.dev/en/stable/reference/generated/cupy.linalg.svd.html |
| 稀疏矩阵分解论文 | https://dl.acm.org/doi/10.1145/1401890.1401944 |
| IEEE浮点标准 | https://ieeexplore.ieee.org/document/8766229 |
| 量子算法综述 | https://arxiv.org/abs/1804.03719 |
| GPU加速原理 | https://developer.nvidia.com/cuda-toolkit |
| 矩阵分解教程 | https://www.cs.cmu.edu/~venkatg/teaching/CStheory-infoage/book-chapter-4.pdf |
这篇文章包含了详细的原理介绍、代码示例、源码注释以及案例等。希望这对您有帮助。如果有任何问题请随私信或评论告诉我。
相关文章:

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】1.27 线性代数王国:矩阵分解实战指南
1.27 线性代数王国:矩阵分解实战指南 #mermaid-svg-JWrp2JAP9qkdS2A7 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-JWrp2JAP9qkdS2A7 .error-icon{fill:#552222;}#mermaid-svg-JWrp2JAP9qkdS2A7 .erro…...

Kafka常见问题之 java.io.IOException: Disk error when trying to write to log
文章目录 Kafka常见问题之 java.io.IOException: Disk error when trying to write to log1. 问题概述2. 问题排查方向(1)磁盘空间不足(2)磁盘 I/O 故障(3)Kafka 日志文件损坏(4)Kaf…...

libOnvif通过组播不能发现相机
使用libOnvif库OnvifDiscoveryClient类, auto discovery new OnvifDiscoveryClient(QUrl(“soap.udp://239.255.255.250:3702”), cb.Build()); 会有错误: end of file or no input: message transfer interrupted or timed out(30 sec max recv delay)…...
 :Table API SQL (一) 概览)
Flink (十二) :Table API SQL (一) 概览
Apache Flink 有两种关系型 API 来做流批统一处理:Table API 和 SQL。Table API 是用于 Scala 和 Java 语言的查询API,它可以用一种非常直观的方式来组合使用选取、过滤、join 等关系型算子。Flink SQL 是基于 Apache Calcite 来实现的标准 SQL。无论输入…...

FFmpeg(7.1版本)的基本组成
1. 前言 FFmpeg 是一个非常流行的开源项目,它提供了处理音频、视频以及其他多媒体内容的强大工具。FFmpeg 包含了大量的库,可以用来解码、编码、转码、处理和播放几乎所有类型的多媒体文件。它广泛用于视频和音频的录制、转换、流媒体传输等领域。 2. F…...

基于微信小程序的辅助教学系统的设计与实现
标题:基于微信小程序的辅助教学系统的设计与实现 内容:1.摘要 摘要:随着移动互联网的普及和微信小程序的兴起,基于微信小程序的辅助教学系统成为了教育领域的一个新的研究热点。本文旨在设计和实现一个基于微信小程序的辅助教学系统,以提高教…...

单片机基础模块学习——超声波传感器
一、超声波原理 左边发射超声波信号,右边接收超声波信号 左边的芯片用来处理超声波发射信号,中间的芯片用来处理接收的超声波信号 二、超声波原理图 T——transmit 发送R——Recieve 接收 U18芯片对输入的N_A1信号进行放大,然后输入给超声…...

HTML<hgroup>标签
例子: 使用hgroup元素标记标题和段落是相关的: <hgroup> <h2>Norway</h2> <p>The land with the midnight sun.</p> </hgroup> 定义和用法: 标签<hgroup>用于包围标题和一个或多个<p&g…...

C++并发编程指南08
以下是经过优化排版后的5.3节内容,详细解释了C中的同步操作和强制排序机制。每个部分都有详细的注释和结构化展示。 文章目录 5.3 同步操作和强制排序假设场景示例代码 5.3.1 同步发生 (Synchronizes-with)基本思想 5.3.2 先行发生 (Happens-before)单线程环境多线程…...
Spring Boot - 数据库集成03 - 集成Mybatis
Spring boot集成Mybatis 文章目录 Spring boot集成Mybatis一:基础知识1:什么是MyBatis2:为什么说MyBatis是半自动ORM3:MyBatis栈技术演进3.1:JDBC,自行封装JDBCUtil3.2:IBatis3.3:My…...

python:洛伦兹变换
洛伦兹变换(Lorentz transformations)是相对论中的一个重要概念,特别是在讨论时空的变换时非常重要。在四维时空的背景下,洛伦兹变换描述了在不同惯性参考系之间如何变换时间和空间坐标。在狭义相对论中,洛伦兹变换通常…...

“星门计划对AI未来的意义——以及谁将掌控它”
“星门计划对AI未来的意义——以及谁将掌控它” 图片由DALL-E 3生成 就在几天前,唐纳德特朗普宣布了“星门计划”,OpenAI随即跟进,分享了更多细节。他们明确表示,计划在未来四年内投资5000亿美元,在美国为OpenAI构建一…...

为什么“记住密码”适合持久化?
✅ 特性 1:应用重启后仍需生效 记住密码的本质是长期存储用户的登录凭证(如用户名、密码、JWT Token),即使用户关闭应用、重启设备,仍然可以自动登录。持久化存储方案: React Native 推荐使用 AsyncStorag…...

国产SiC碳化硅功率器件技术成为服务器电源升级的核心引擎
在服务器电源应用中,国产650V碳化硅(SiC)MOSFET逐步取代传统超结(Super Junction, SJ)MOSFET,其核心驱动力源于SiC材料在效率、功率密度、可靠性和长期经济性上的显著优势,叠加产业链成熟与政策…...
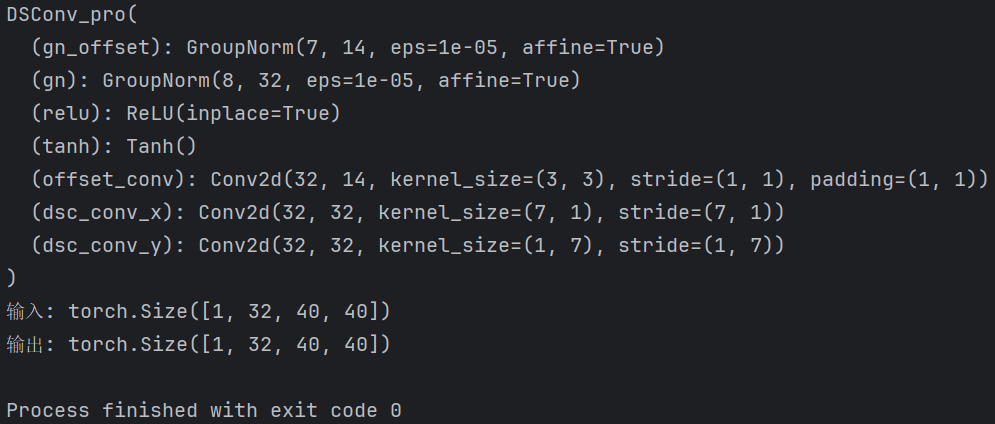
【Block总结】动态蛇形卷积,专注于细长和弯曲的局部结构|即插即用
论文信息 标题: Dynamic Snake Convolution based on Topological Geometric Constraints for Tubular Structure Segmentation 作者: 戚耀磊、何宇霆、戚晓明、张媛、杨冠羽 会议: 2023 IEEE/CVF International Conference on Computer Vision (ICCV) 发表时间: 2023年10月…...

Spring MVC 框架:构建高效 Java Web 应用的利器
Java学习资料 Java学习资料 Java学习资料 一、引言 在 Java Web 开发领域,Spring MVC 框架是一颗耀眼的明星。它作为 Spring 框架家族的重要成员,为开发者提供了一套强大而灵活的解决方案,用于构建 Web 应用程序。Spring MVC 遵循模型 - 视…...
新鲜速递:DeepSeek-R1开源大模型本地部署实战—Ollama + MaxKB 搭建RAG检索增强生成应用
在AI技术快速发展的今天,开源大模型的本地化部署正在成为开发者们的热门实践方向。最火的莫过于吊打OpenAI过亿成本的纯国产DeepSeek开源大模型,就在刚刚,凭一己之力让英伟达大跌18%,纳斯达克大跌3.7%,足足是给中国AI产…...
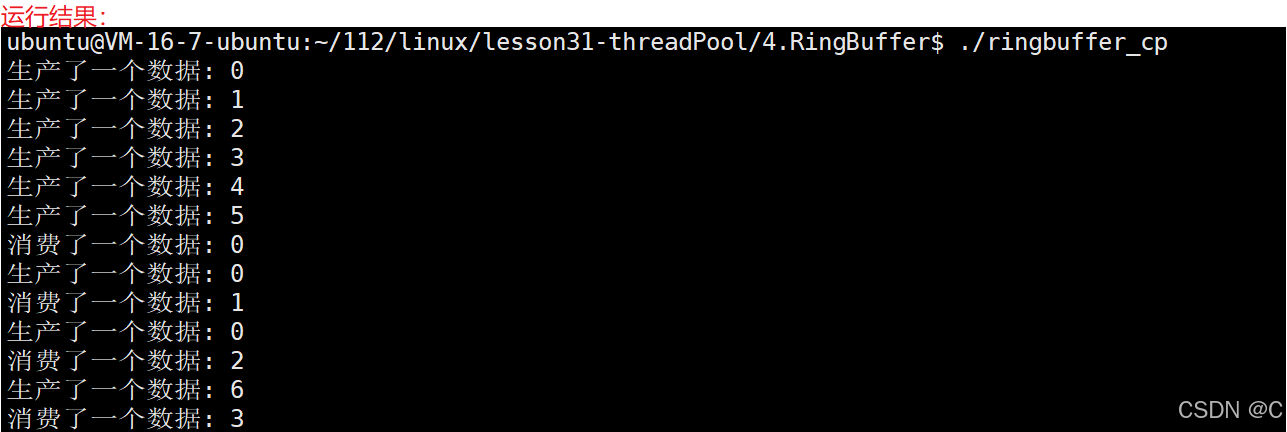
Linux_线程同步生产者消费者模型
同步的相关概念 同步:在保证数据安全的前提下,让线程能够按照某种特定的顺序访问临界资源,从而有效避免饥饿问题,叫做同步竞态条件:因为时序问题,而导致程序异常,我们称之为竞态条件。 同步的…...
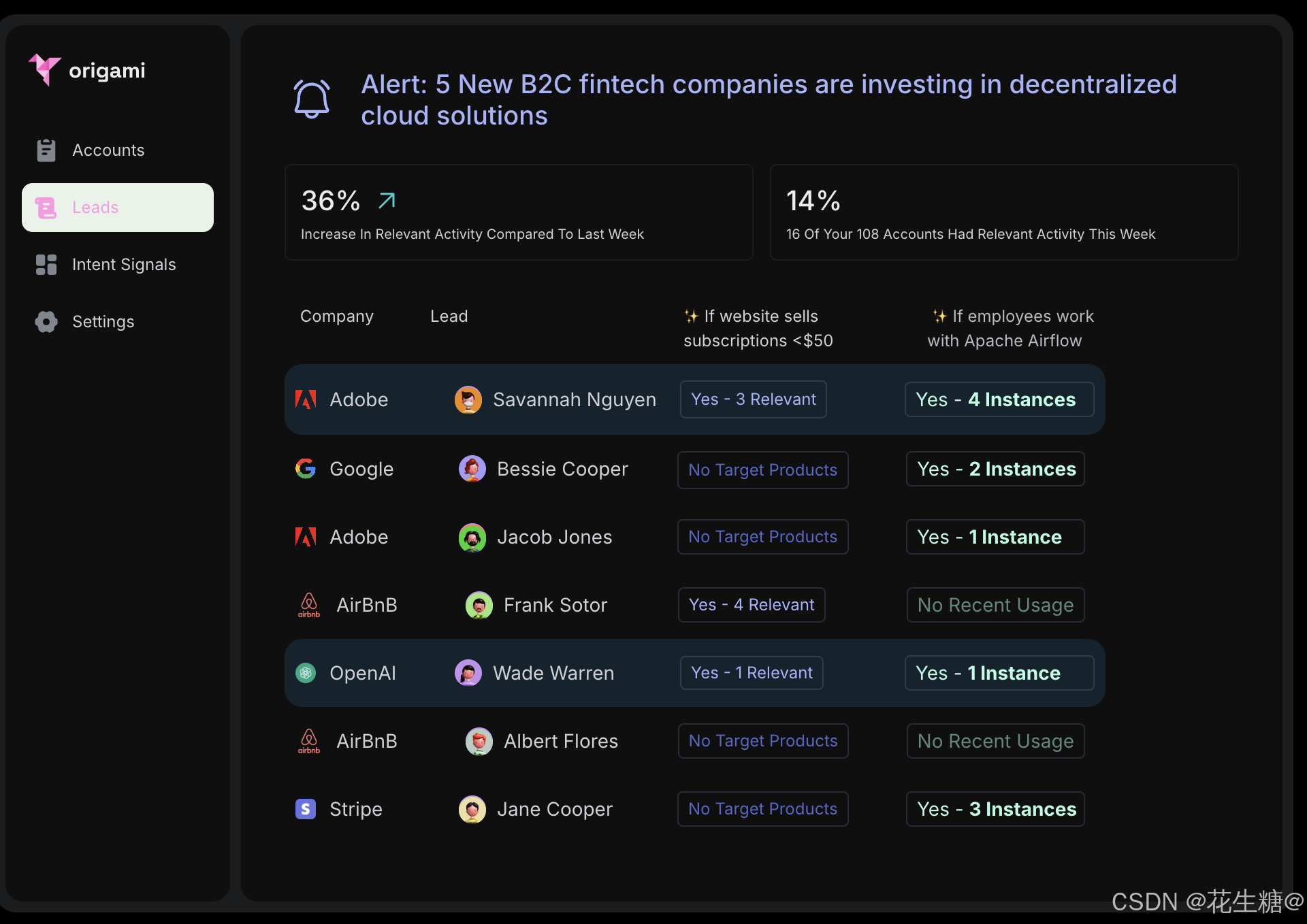
Origami Agents:通过AI驱动的研究工具提升B2B销售效率
在当今竞争激烈的商业环境中,B2B销售团队面临着巨大的挑战,如何高效地发现潜在客户并进行精准的外展活动成为关键。Origami Agents通过其创新的AI驱动研究工具,正在彻底改变这一过程。本文将深入探讨Origami Agents的产品特性、技术架构以及其快速增长背后的成功因素。 一、…...

linux的/proc 和 /sys目录差异
/proc 和 /sys 都是Linux系统中用于提供系统信息和进行系统配置的虚拟文件系统,但它们的原理并不完全一样,以下是具体分析: 目的与功能 /proc :主要用于提供系统进程相关信息以及内核运行时的一些参数等,可让用户和程…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
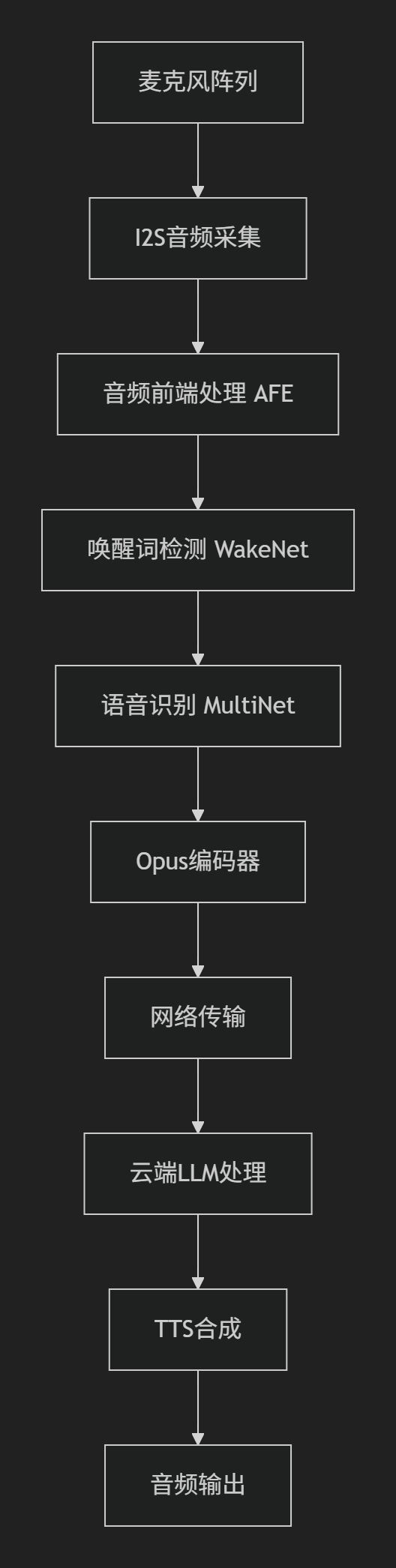
SDU棋界精灵——硬件程序ESP32实现opus编码
一、 音频处理框架 该项目基于Espressif的音频处理框架构建,核心组件包括 ESP-ADF 和 ESP-SR,以下是完整的音频处理框架实现细节: 1.核心组件 (1) 音频前端处理 (AFE - Audio Front-End) main/components/audio_pipeline/afe_processor.c功能: 声学回声…...
