Starlink卫星动力学系统仿真建模第九讲-滑模(SMC)控制算法原理简介及卫星控制应用
滑模控制(Sliding Mode Control)算法详解
一、基本原理
滑模控制(Sliding Mode Control, SMC)是一种变结构控制方法,通过设计一个滑模面(Sliding Surface),迫使系统状态在有限时间内到达该面,并在滑模面上沿预定轨迹滑动至平衡点。其核心特点是强鲁棒性,能够有效抑制参数不确定性、模型误差和外部扰动。

关键步骤:
-
滑模面设计:
定义滑模面 ( s(t) = 0 ),通常选择误差及其导数的线性组合。
例如,对二阶系统:
[
s(t) = \dot{e}(t) + \lambda e(t) \quad (\lambda > 0)
]
其中 ( e(t) = x_{\text{desired}} - x(t) )。 -
控制律设计:
设计控制输入 ( u(t) ),使得系统状态在有限时间内收敛到滑模面,并保持滑动。
控制律一般形式:
[
u(t) = u_{\text{eq}}(t) + u_{\text{sw}}(t)
]- 等效控制 ( u_{\text{eq}} ):抵消系统动态,保证在滑模面上滑动。
- 切换控制 ( u_{\text{sw}} ):抑制扰动,通常包含符号函数 ( \text{sign}(s) )。
-
稳定性分析:
通过李雅普诺夫函数证明 ( \dot{V}(s) \leq -\eta |s| ),确保有限时间收敛。
二、分类
-
传统滑模控制
- 控制律包含不连续项(如符号函数),易引起抖振(高频振荡)。
- 示例:
[
u(t) = K \cdot \text{sign}(s)
]
-
高阶滑模控制
- 通过高阶导数平滑抖振,如超螺旋算法(Super-Twisting Algorithm)。
- 示例(二阶滑模):
[
u(t) = -k_1 |s|^{1/2} \text{sign}(s) + v, \quad \dot{v} = -k_2 \text{sign}(s)
]
-
终端滑模控制
- 引入非线性滑模面,实现有限时间收敛。
- 示例:
[
s(t) = \dot{e} + \beta e^{q/p} \quad (\beta > 0, , q < p \text{为正奇数})
]
三、代码实现(Python)
以二阶系统为例,设计传统滑模控制器。
import numpy as np
import matplotlib.pyplot as pltclass SlidingModeController:def __init__(self, lambda_, K, dt):self.lambda_ = lambda_ # 滑模面参数self.K = K # 切换增益self.dt = dt # 采样时间self.prev_error = 0.0def compute(self, desired, actual, actual_derivative):error = desired - actualerror_derivative = (error - self.prev_error) / self.dtself.prev_error = error# 滑模面 s = error_derivative + lambda * errors = error_derivative + self.lambda_ * error# 控制律: u = K * sign(s)u = self.K * np.sign(s)return u# 系统模型(二阶系统)
def system_model(x, dx, u, dt):# 假设系统动力学: ddx = -2*dx - 3*x + u + 扰动ddx = -2 * dx - 3 * x + u + 0.5 * np.sin(10 * x) # 加入扰动dx_new = dx + ddx * dtx_new = x + dx_new * dtreturn x_new, dx_new# 参数初始化
lambda_ = 2.0
K = 5.0
dt = 0.01
controller = SlidingModeController(lambda_, K, dt)# 仿真
desired = 1.0
x, dx = 0.0, 0.0
time = np.arange(0, 10, dt)
x_history = []for t in time:u = controller.compute(desired, x, dx)x_new, dx_new = system_model(x, dx, u, dt)x, dx = x_new, dx_newx_history.append(x)# 绘图
plt.plot(time, x_history, label='Actual')
plt.plot(time, [desired]*len(time), 'r--', label='Desired')
plt.xlabel('Time (s)')
plt.ylabel('Position')
plt.legend()
plt.show()
四、在卫星姿态控制中的使用示例
场景
控制卫星三轴姿态(俯仰角、偏航角、滚动角),使其跟踪目标姿态角。
动力学模型(以俯仰轴为例):
[
J \ddot{\theta} = u + d(t)
]
- ( J ):转动惯量
- ( \theta ):俯仰角
- ( u ):控制力矩
- ( d(t) ):外部扰动(如太阳辐射压力)。
滑模控制设计
-
定义误差:
[
e = \theta_{\text{desired}} - \theta
] -
滑模面:
[
s = \dot{e} + \lambda e \quad (\lambda > 0)
] -
控制律:
[
u = J \left( \ddot{\theta}_{\text{desired}} + \lambda \dot{e} \right) - K \cdot \text{sign}(s)
]
(包含等效控制和切换项)
代码片段(简化)
class SatelliteSMController:def __init__(self, lambda_, K, J, dt):self.lambda_ = lambda_self.K = Kself.J = Jself.dt = dtself.prev_error = 0.0def compute(self, theta_desired, theta, dtheta):error = theta_desired - thetaerror_derivative = (error - self.prev_error) / self.dtself.prev_error = errors = error_derivative + self.lambda_ * erroru_eq = self.J * (0 + self.lambda_ * error_derivative) # 假设目标角加速度为0u_sw = -self.K * np.sign(s)u = u_eq + u_swreturn u# 卫星姿态动力学仿真
J = 100.0 # 转动惯量
dt = 0.01
controller = SatelliteSMController(lambda_=1.5, K=50, J=J, dt=dt)
theta, dtheta = 0.0, 0.0
theta_desired = np.deg2rad(30) # 目标30度for _ in range(1000):u = controller.compute(theta_desired, theta, dtheta)ddtheta = (u + 10 * np.sin(2 * np.pi * 0.1 * _ * dt)) / J # 控制输入 + 扰动dtheta += ddtheta * dttheta += dtheta * dt
五、关键问题与改进
-
抖振抑制:
- 使用饱和函数 ( \text{sat}(s/\phi) ) 替代符号函数。
- 采用高阶滑模(如超螺旋算法)。
-
参数选择:
- ( \lambda ) 决定滑模面收敛速度。
- ( K ) 需大于扰动上界。
六、总结
- 优点:强鲁棒性,适用于复杂扰动和模型不确定性场景(如航天器、无人机)。
- 缺点:抖振可能影响执行机构寿命。
- 应用扩展:结合自适应控制、模糊逻辑,进一步提升性能。
相关文章:

Starlink卫星动力学系统仿真建模第九讲-滑模(SMC)控制算法原理简介及卫星控制应用
滑模控制(Sliding Mode Control)算法详解 一、基本原理 滑模控制(Sliding Mode Control, SMC)是一种变结构控制方法,通过设计一个滑模面(Sliding Surface),迫使系统状态在有限时间内…...

JVM相关面试题
1. 类加载与双亲委派机制 聊一下你对类加载器的理解。 类加载器是JVM用来加载类文件到内存的组件。它负责将字节码文件解析为java.lang.Class实例,并存储到运行时数据区的方法区中。类加载器分为Bootstrap ClassLoader、Extension ClassLoader和Application ClassLo…...

WiFi定位:宠物安全的“秘密武器”
从「全网寻狗」到「实时掌控」的进化史 凌晨三点收到邻居转发的「寻狗启事」,配图里的金毛犬项圈上赫然挂着某品牌定位器 —— 这样的魔幻场景在养宠圈并不罕见。随着宠物经济突破 3000 亿规模,智能定位器早已从「小众玩具」变成「刚需装备」。但你知道…...

【git】【reset全解】Git 回到上次提交并处理提交内容的不同方式
Git 回到上次提交并处理提交内容的不同方式 在 Git 中,若要回到上次提交并对提交内容进行不同处理,可使用 git reset 命令搭配不同选项来实现。以下为你详细介绍操作步骤及各选项的作用。 1. 查看提交历史 在操作之前,可通过以下命令查看提…...

【leetcode hot 100 11】移动零
一、暴力解法:两个 for 循环,外层循环遍历所有可能的左边界,内层循环遍历所有可能的右边界 class Solution {public int maxArea(int[] height) {int max_area0;for(int i0; i<height.length; i){for(int ji1; j<height.length; j){in…...

DeepSeek 部署实战:Ollama + 多客户端 + RAG
DeepSeek 部署实战:Ollama 多客户端 RAG 一、前置条件 (一)硬件要求 GPU:强烈建议使用 NVIDIA RTX 3090 或更高型号,显存至少 24GB。小显存跑大模型会遇到诸多问题,本人亲测 2080Ti 跑模型体验不佳。内…...

Linux通过设备名称如何定位故障硬盘
因为ceph集群的服务器硬盘都是直通的,当我们发现有硬盘存储坏道需要更换硬盘,但是因为盘序可能不是连续的,无法定位服务器上那块硬盘是故障的,如果冒然测试可能把正常的硬盘拔出,得不偿失,所以就写一下我定…...

大模型基础概念之神经网络宽度
在大模型中,神经网络宽度是提升模型容量的核心手段之一,与深度、数据规模共同构成性能的三大支柱。合理增加宽度可显著增强模型表达能力,但需结合正则化、硬件优化和结构设计进行平衡。未来趋势可能包括动态宽度调整、稀疏化宽度设计(如MoE)以及更高效宽度-深度复合缩放策…...

数据开发的简历及面试
简历 个人信息: 邮箱别写QQ邮箱, 写126邮箱/189邮箱等 学历>>本科及以上写,大专及以下不写 专业>>非计算机专业不写 政治面貌>>党员写, 群众不用写 掌握的技能: 精通 > 熟悉 > 了解 专业工具: 大数据相关的 公司: 如果没有可以写的>>金融服…...

数据存储:一文掌握存储数据到ElasticSearch详解
文章目录 一、Elasticsearch简介二、Python与Elasticsearch交互2.1 安装必要的库2.2 连接到Elasticsearch服务器 三、数据准备四、创建索引(可选)五、存储数据5.1 单个文档索引5.2 批量索引 六、查询数据七、更新和删除数据7.1 更新文档7.2 删除文档 八、…...
)
Pytorch使用手册--将 PyTorch 模型导出为 ONNX(专题二十六)
注意 截至 PyTorch 2.1,ONNX 导出器有两个版本。 torch.onnx.dynamo_export 是最新的(仍处于测试阶段)导出器,基于 PyTorch 2.0 发布的 TorchDynamo 技术。 torch.onnx.export 基于 TorchScript 后端,自 PyTorch 1.2.0 起可用。 一、torch.onnx.dynamo_export使用 在 60 …...

Vue2+Element实现Excel文件上传下载预览
目录 一、需求背景 二、落地实现 1.文件上传 图片示例 HTML代码 业务代码 2.文件下载 图片示例 方式一:代码 方式二:代码 3.文件预览 图片示例 方式一:代码 方式二:代码 一、需求背景 在一个愉快的年后ÿ…...

物联网平台建设方案一
系统概述 构建物联网全域支撑服务能力,为实现学院涵盖物联网设备的全面感知、全域互联、全程智控、全域数字基底、全过程统筹管理奠定基础,为打造智能化提供坚实后台基石。 物联网平台向下接入各种传感器、终端和网关,向上通过开放的实施分…...

机器学习破局指南:零基础6个月系统训练计划
以下是为零基础学习者制定的「机器学习」系统学习计划(含学习路径资源推荐),分为6个阶段,建议学习周期4-6个月: 一、基础准备阶段(1-2周) 目标:掌握必要数学工具与编程基础 数学基础…...

mmdetection框架下使用yolov3训练Seaships数据集
之前复现的yolov3算法采用的是传统的coco数据集,这里我需要在新的数据集上跑,也就是船舶检测方向的SeaShips数据集,这里给出教程。 Seaships论文链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp&arnumber8438999 一、…...
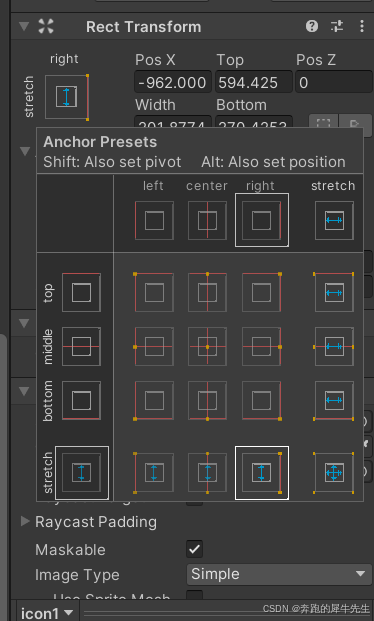
unity学习52:UI的最基础组件 rect transform,锚点anchor,支点/轴心点 pivot
目录 1 image 图像:最简单的UI 1.1 图像的基本属性 1.2 rect transform 1.3 image的component: 精灵 → 图片 1.4 修改颜色color 1.5 修改材质 1.6 raycast target 1.7 maskable 可遮罩 1.8 imageType 1.9 native size 原生大小 2 rect transform 2.1 …...

STM32MP15-FSMP1A单片机移植Linux系统platform总线驱动
之前在该单片机下移植的Linux驱动是学习过程中,对Linux内核驱动的引导学习,接下来才是比较正常的驱动开发。 在Linux内核中,对于驱动的处理,一般会通过总线进行设备信息和设备驱动的匹配,来达到自动检测外设连接系统以…...
)
Java 常见的面试题(设计模式)
一、说一下你熟悉的设计模式? **设计模式:**是一套被反复使用的代码设计经验的总结(情境中一个问题经过证实的一个解决方案)。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性。设计模式使人们可以更加简…...

机器学习3-聚类
1 聚类解决的问题 知识发现,发现事物之间的潜在关系异常值检测特征提取 数据压缩的例子新闻自动分组、用户分群、图像分割、像素压缩等等 2 与监督学习比较 监督学习是需要给定X、Y,X为特征,Y为标签,选择模型,学习&a…...

html中的css
css (cascading style sheets,串联样式表,也叫层叠样式表) css规范一般约定: 1.存放CSS样式文件的目录一般命名为style或css。 2.在项目初期,会把不同类别的样式放于不同的CSS文件,是为了CSS编…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
