2023/2/13 蓝桥备战acwing刷题(set的使用、简单推个不等式+差分、快速幂、01背包模板回顾、类似01背包的题)
4454未初始化警告
set计数
#include<iostream>
#include<set>
using namespace std;int main(){int n,m;cin>>n>>m;set<int> s;int res = 0;s.insert(0);while(m--){int l,r;cin>>l>>r;if(s.count(r)==0){res++;}s.insert(l);}cout<<res<<endl;return 0;
}
4455出行计划
有题目可得不等式
q>=t−c+1−kq>=t-c+1-kq>=t−c+1−k
q<=t−kq<=t-kq<=t−k
但是如果正常的遍历会出现O(n2)O(n^2)O(n2)的复杂度
所以要优化的话,可以这么搞:
因为公式已知,我们可以得到能正常参加各个计划的q的区间
对这个区间都加一
最后询问时直接O(1)的访问就行
所以区间加法,用差分
细节是注意负值的处理,防止越界
#include<iostream>
using namespace std;
const int maxx = 2e5+10;struct Node{int t;int c;
};Node node[maxx];
int d[maxx];int main(){int m,k,n;cin>>n>>m>>k;//q+k>=t-c+1,q+k<=tfor(int i=0;i<n;i++){int t,c;cin>>t>>c;int l = t+1-c-k;int r = t-k;//注意处理一下负值l = max(l,1);if(r>0){d[l]++,d[r+1]--;}}for(int i=1;i<maxx;i++){d[i]=d[i-1]+d[i];}while(m--){int q;cin>>q;cout<<d[q]<<endl;}return 0;
}
4728乘方
用快速幂做的,注意用ull,ll会有问题
#include<iostream>
#include<cmath>
using namespace std;
typedef unsigned long long ll;
const ll INF = 1e9;ll fastpow(ll a,ll b){ll res = 1;while(b>=1){if(b%2==1){res*=a;}if(res>INF){return 0;}b/=2;a = a*a;}return res;
}int main(){ll a,b;cin>>a>>b;ll res = fastpow(a,b);if(res==0)cout<<"-1"<<endl;else cout<<res<<endl;return 0;
}
2、01背包
#include<iostream>
using namespace std;
const int maxx = 1e4+10;int dp[maxx][maxx];
int v[maxx];
int w[maxx];int main(){int N,V;cin>>N>>V;for(int i=1;i<=N;i++){cin>>v[i]>>w[i];}for(int i=1;i<=N;i++){for(int j=0;j<=V;j++){if(j<v[i]){dp[i][j] = dp[i-1][j];}else{dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);}}}cout<<dp[N][V]<<endl;return 0;
}
4700 何以包邮(说实话没懂)
给出x,给出一个价格数组,要求挑一些数出来,总和m>=xm>=xm>=x,且尽量小
想到01背包,它是和要小于一个值(背包大小),所以我们这里可以采用加负号反向
即当总和不超过sum-x时尽可能大
注意要反向遍历,相当于不断分解
#include<iostream>
using namespace std;
const int maxlen=40;
const int maxx = 3e5+20;int dp[maxx];
int a[maxlen];int main(){int n,x;cin>>n>>x;int sum=0;for(int i=1;i<=n;i++){cin>>a[i];sum+=a[i];}int res = 0;for(int i=1;i<=n;i++){for(int j=sum-x;j>=a[i];j--){dp[j]=max(dp[j],dp[j-a[i]]+a[i]);res = max(res,dp[j]);}}cout<<sum-dp[sum-x]<<endl;return 0;
}
相关文章:
)
2023/2/13 蓝桥备战acwing刷题(set的使用、简单推个不等式+差分、快速幂、01背包模板回顾、类似01背包的题)
4454未初始化警告 set计数 #include<iostream> #include<set> using namespace std;int main(){int n,m;cin>>n>>m;set<int> s;int res 0;s.insert(0);while(m--){int l,r;cin>>l>>r;if(s.count(r)0){res;}s.insert(l);}cout<…...

【情人节专属】AI一键预测你和Ta的CP值
如何预测你和心仪的Ta有没有夫妻相?基于华为云ModelArts开发的【一键预测你和Ta的CP值】Demo帮你预测CP指数。该模型利用ssim算法综合计算五官特征相似程度,从而得出CP值。//夫妻相的原理在当今心理学、生物学仍有很大争议,夫妻相指数高并不意…...
一文浅谈sql中的 in与not in,exists与not exists的区别以及性能分析
文章目录1. 文章引言2. 查询对比2.1 in和exists2.2 not in 和not exists2.3 in 与 的区别3. 性能分析3.1 in和exists3.2 NOT IN 与NOT EXISTS4. 重要总结1. 文章引言 我们在工作的过程中,经常使用in,not in,exists,not exists来…...
2023前端面试题——JS篇
1.判断 js 类型的方式 1. typeof 可以判断出’string’,‘number’,‘boolean’,‘undefined’,‘symbol’ 但判断 typeof(null) 时值为 ‘object’; 判断数组和对象时值均为 ‘object’ 2. instanceof 原理是 构造函数的 prototype 属性是否出现在对象的原型链中的任何位置 …...
微服务中API网关的作用是什么?
目录 什么是API网关? 为什么要用API网关? API网关架构 API网关是如何实现这些功能的? 协议转换 链式处理 异步请求 什么是API网关? Api网关是微服务的重要组成部分,封装了系统内部的复杂结构,客户端…...

python爬虫--xpath模块简介
一、前言 前两篇博客讲解了爬虫解析网页数据的两种常用方法,re正则表达解析和beautifulsoup标签解析,所以今天的博客将围绕另外一种数据解析方法,它就是xpath模块解析,话不多说,进入内容: 一、简介 XPat…...

【论文阅读】基于意图的网络(Intent-Based Networking,IBN)研究综述
IBN研究综述一、IBN体系结构1.1 体系结构:1.2 闭环流程:1.3 IBN的自动化程度(逐步向前演进):二、IBN 的实现方式2.1 意图获取:2.1.1 YANG、NEMO2.1.2 Frenetic、NetKAT、LAI2.2 意图转译:2.2.1 iNDIRA系统2.2.2 基于模…...
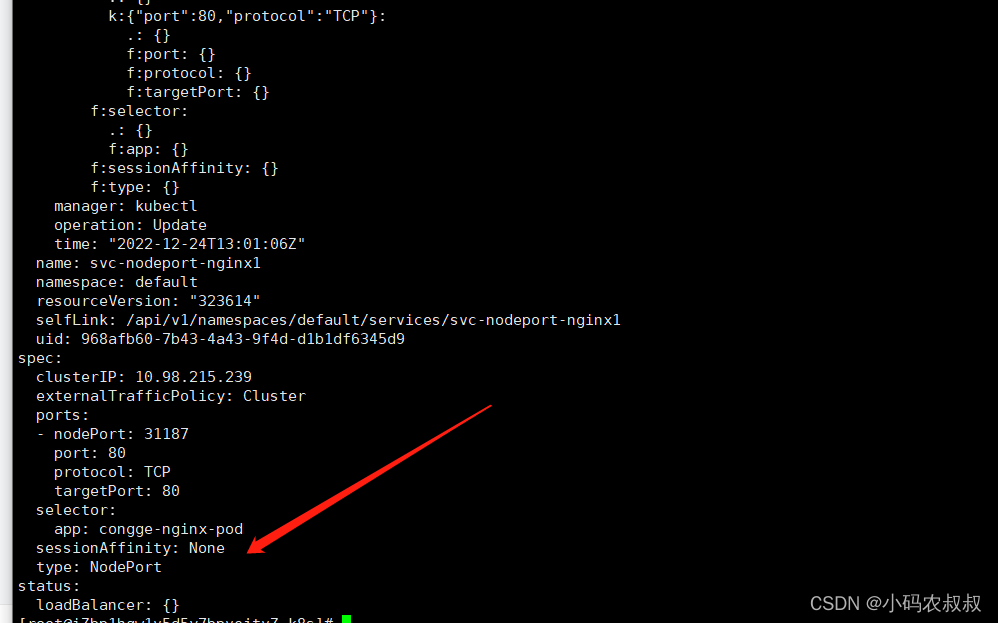
【云原生kubernetes】k8s service使用详解
一、什么是服务service? 在k8s里面,每个Pod都会被分配一个单独的IP地址,但这个IP地址会随着Pod的销毁而消失,重启pod的ip地址会发生变化,此时客户如果访问原先的ip地址则会报错 ; Service (服务)就是用来解决这个问题的…...

Python 数据可视化的 3 大步骤,你知道吗?
Python实现可视化的三个步骤: 确定问题,选择图形转换数据,应用函数参数设置,一目了然 1、首先,要知道我们用哪些库来画图? matplotlib Python中最基本的作图库就是matplotlib,是一个最基础的Python可视…...

CSS基础:盒子模型和浮动
盒子模型 所有HTML元素可以看作盒子,在CSS中,"box model"这一术语是用来设计和布局时使用 CSS盒模型本质上是一个盒子,封装HTML元素。 它包括:外边距(margin),边框(bord…...
OpenHarmony使用Socket实现一个TCP服务端详解
点击获取BearPi-HM_Nano源码 ,以D4_iot_tcp_server为例: 点击查看:上一篇关于socket udp实现的解析 查看 TCPServerTask 方法实现: static void TCPServerTask(void) {//连接WifiWifiConnect("TP-LINK_65A8",...

kafka监控工具安装和使用
1. KafkaOffsetMonitor 该监控是基于一个jar包的形式运行,部署较为方便。只有监控功能,使用起来也较为安全(1)消费者组列表 (2)查看topic的历史消费信息. (3)每个topic的所有parition列表(topic,pid,offset,logSize,lag,owner) (4)对consumer消费情况进…...

近期工作感悟
从应届生变为社畜已经半年了,在这里吐槽一下自己的所想给自己看。 首先是心理层面上的,初期大大增加的压力。 我觉得应届生能够来到大厂的,基本都是在大学有去规划学习,对自己技能比较认可的。比如我在学校自学游戏开发ÿ…...
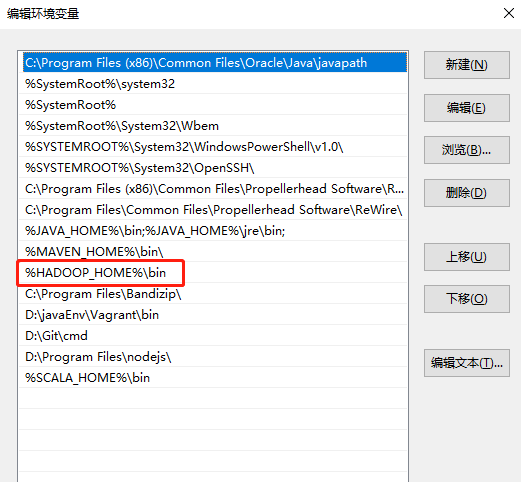
大数据框架之Hadoop:HDFS(三)HDFS客户端操作(开发重点)
3.1 HDFS客户端环境准备 1.根据自己电脑的操作系统拷贝对应的编译后的hadoop jar包到非中文路径(例如:D:\javaEnv\hadoop-2.77),如下图所示。 2.配置HADOOP_HOME环境变量,如下图所示。 3&#…...
多模式支持无线监控技术:主动式定位、被动式定位
物联网空间信息与数字技术发展至今,已经催生了一大批优秀的践行者。在日常与商业应用中,室内外定位领域依托于这一技术的发展,更是在近几年风光无限。但是并不是说室内定位与室外定位都已经相当成熟,相对来说,室内定位…...
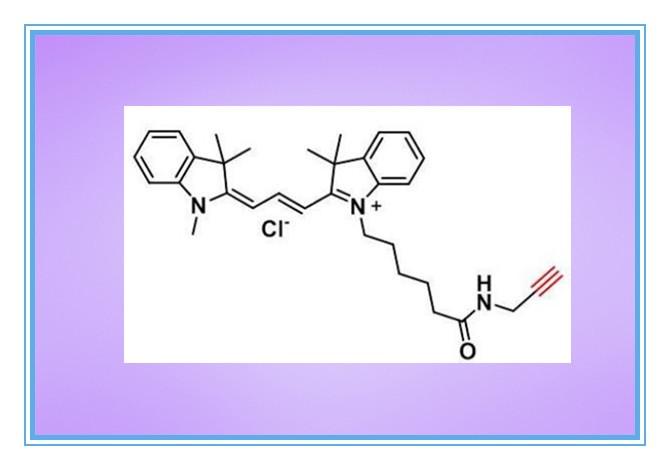
Cy5 Alkyne,1223357-57-0,花青素Cyanine5炔基,氰基5炔烃
CAS号:1223357-57-0 | 英文名: Cyanine5 alkyne,Cy5 Alkyne | 中文名:花青素CY5炔基CASNumber:1223357-57-0Molecular formula:C35H42ClN3OMolecular weight:556.19Purity:95%Appear…...
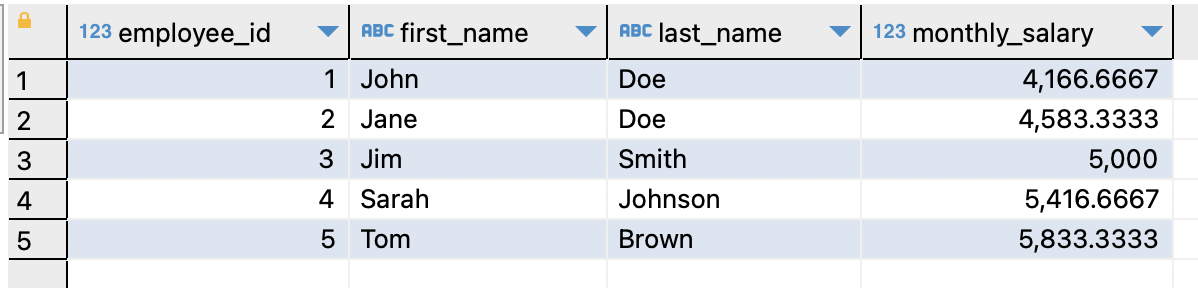
【MySQL】MySQL 中 WITH 子句详解:从基础到实战示例
文章目录一、什么是 WITH 子句1. 定义2.用途二、WITH 子句的语法和用法1.语法2.使用示例3.优点三、总结"梦想不会碎,只有被放弃了才会破灭。" "Dreams wont break, only abandoned will shatter."一、什么是 WITH 子句 1. 定义 WITH 子句是 M…...
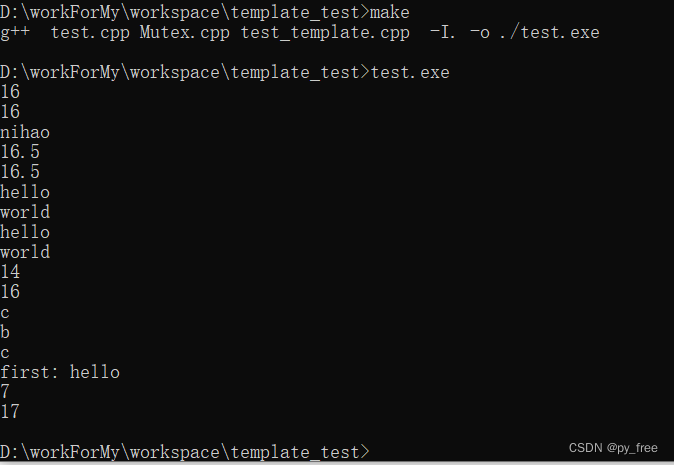
c/c++开发,无可避免的模板编程实践(篇一)
一、c模板 c开发中,在声明变量、函数、类时,c都会要求使用指定的类型。在实际项目过程中,会发现很多代码除了类型不同之外,其他代码看起来都是相同的,为了实现这些相同功能,我们可能会进行如下设计…...

mulesoft MCIA 破釜沉舟备考 2023.02.13.04
mulesoft MCIA 破釜沉舟备考 2023.02.13.03 1. An integration Mule application consumes and processes a list of rows from a CSV file.2. One of the backend systems involved by the API implementation enforces rate limits on the number of request a particle clie…...
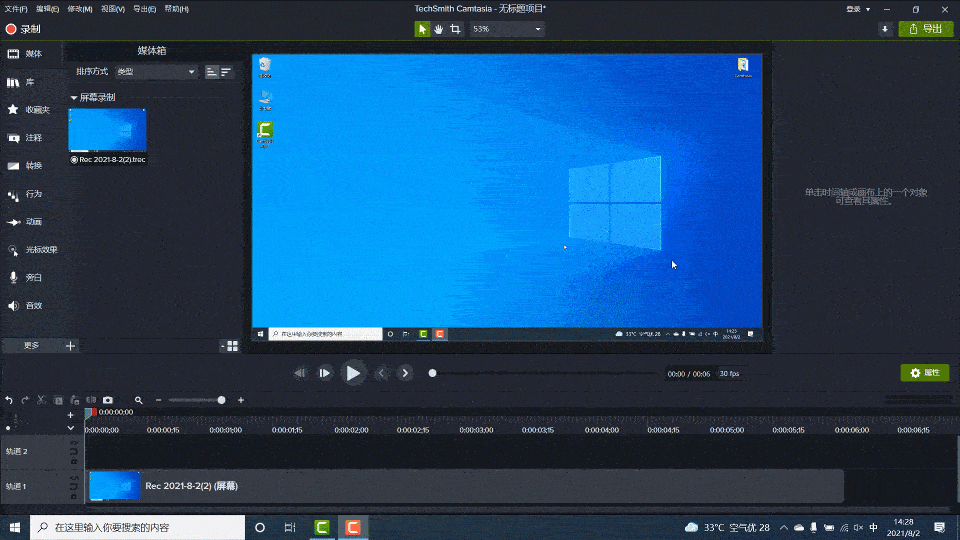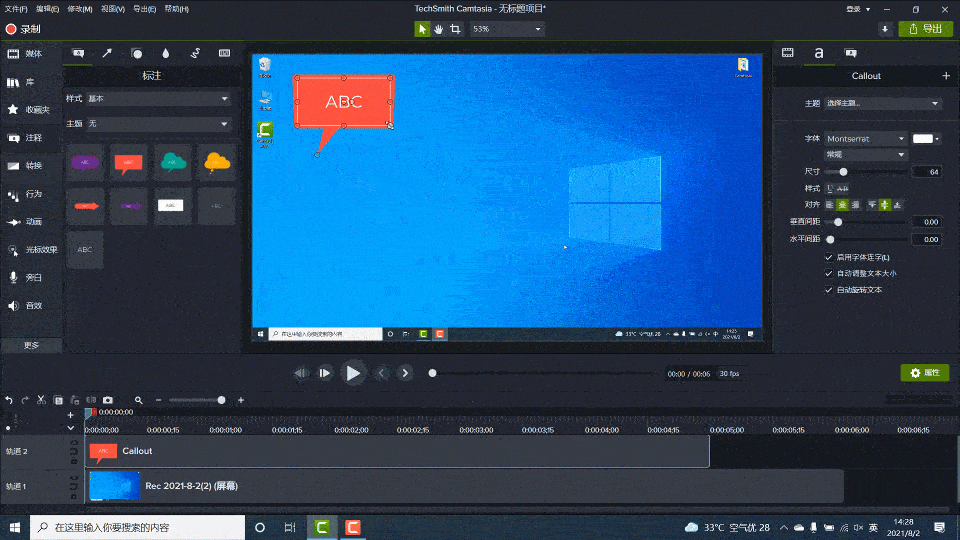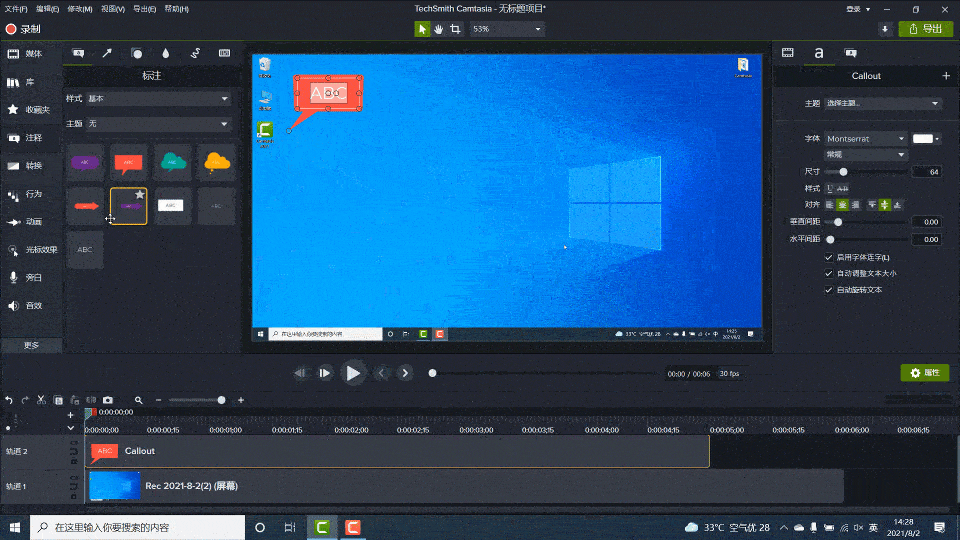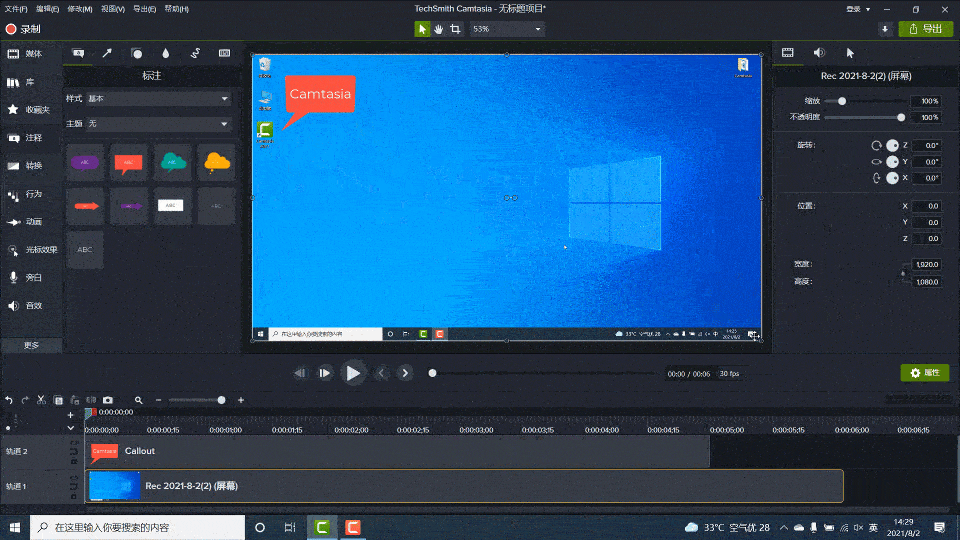
Camtasia2023最新版本新功能及快捷键教程
使用Camtasia,您可以毫不费力地在计算机的显示器上录制专业的活动视频。除了录制视频外,Camtasia还允许您从外部源将高清视频导入到录制中。Camtasia的独特之处在于它可以创建包含可单击链接的交互式视频,以生成适用于教室或工作场所的动态视…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
