python使用args,kwargs
使用*args, **kwargs
在Python中,*args和**kwargs分别用于在函数定义中处理可变数量的位置参数和关键字参数。这使得您可以在调用函数时传入任意数量的参数,而不需要在函数定义中为每个参数单独声明一个形参。
这里是它们的使用方法:
*args用于处理可变数量的位置参数。当在函数定义中使用*args时,它将所有未显式指定的位置参数收集到一个名为args的元组中。您可以在函数内部遍历这个元组来访问这些参数。
示例:
def my_function(*args):for arg in args:print(arg)my_function(1, 2, 3, 4) # 输出: 1 2 3 4
**kwargs用于处理可变数量的关键字参数。在函数定义中使用**kwargs时,所有未显式指定的关键字参数将被收集到一个名为kwargs的字典中。您可以在函数内部遍历这个字典来访问这些参数。
示例:
def my_function(**kwargs):for key, value in kwargs.items():print(f"{key}: {value}")my_function(name="Alice", age=30, city="New York") # 输出: name: Alice, age: 30, city: New York
您还可以将*args和**kwargs结合起来使用,以处理可变数量的位置参数和关键字参数。
示例:
def my_function(*args, **kwargs):for arg in args:print(arg)for key, value in kwargs.items():print(f"{key}: {value}")my_function(1, 2, 3, name="Alice", age=30, city="New York")
# 输出: 1 2 3, name: Alice, age: 30, city: New York
注意,在使用时,通常省略args和kwargs的名称,只保留前面的星号。但是,这些名称在函数内部是需要的,以便访问传递的参数。
相关文章:

python使用args,kwargs
使用*args, **kwargs 在Python中,*args和**kwargs分别用于在函数定义中处理可变数量的位置参数和关键字参数。这使得您可以在调用函数时传入任意数量的参数,而不需要在函数定义中为每个参数单独声明一个形参。 这里是它们的使用方法: *arg…...

20230408英语学习
Planting This Could Feed Millions and Lock Away Tons of Carbon 食用菌:新型蛋白质来源,还能固碳 The world hungers for more food while wildlife yearns for untouched habitats.So goes the conflict between our seemingly insatiable need for…...
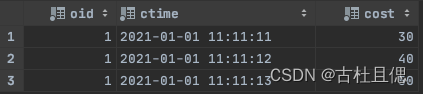
ReplacingMergeTree
在 MergeTree 的基础上,添加了“处理重复数据”的功能,该引擎和MergeTree的不同之处在于它会删除具有相同(区内)排序⼀样的重复项。数据的去重只会在合并的过程中出现。合并会在未知的时间在后台进⾏(⼿动合并),所以你⽆法预先作出计划。有⼀…...
)
Java核心技术知识点笔记—集合(二)
1、树集(TreeSet):是一个有序集合(sorted collection),与散列集类似,但比散列集有所改进。 (1)可以以任意顺序将元素插入到集合中; (2ÿ…...

Sharepoint Online手工迁移方案 | 分享二
目录 前言 1.创建新的目标网站集合 2.备份旧网站集合的内容数据库 3.卸载旧网站集合...

MVC获取当前区域、控制器、Action
控制器中获取: 获取区域名称:RouteData.DataTokens["area"].ToString() 获取控制器名称:RouteData.Values["controller"].ToString() 获取Action名称:RouteData.Values["action"].ToString() 视…...

第十六章 脚手架文件介绍
react项目脚手架文件目录 public ---- 静态资源文件夹 |-------favicon.icon ------ 网站页签图标 |-------index.html -------- 主页面 |-------logo192.png ------- logo图 |-------logo512.png ------- logo图 |-------manifest.json ----- 应用加壳的配置文件 |-------rob…...

基于Clion开发(stm32移植FreeRTOS+LVGL)
嵌入式单片机开发中,通常使用 Keil IAR 或 芯片厂商提供的IDE,这类IDE界面风格还停留在十几年前XP风,代码编辑实在让人难受,所以很多时候笔者都是采用VSCode编辑,然后再用这类IDE下载调试使用,另外像keil 和…...

Python | 蓝桥杯进阶第三卷——动态规划
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——贪心 💝 Python | 蓝桥杯进阶第三卷——动态规划 ✈️ Python | 蓝桥杯进阶…...

蓝桥杯31天真题冲刺|题解报告|第二十九天
大家好,我是snippet,今天是我们刷题的第二十九天,今天主打打比赛,牛客AcWing力扣,今天的牛客是真的有趣,下面是我今天AcWing周赛的题解 目录 一、热身计算 题目链接:4944. 热身计算 - AcWing题…...

[Rust GUI]fltk-rs的helloworld
1、安装VSCode 下载安装VSCode 安装VSCode扩展 rust-analyzer或rust-analyzer(CN) 2、安装Microsoft C 生成工具 访问微软官网下载生成工具,勾选使用 C 的桌面开发之后会自动勾选5个项目 取消勾选以下项目 用于 Windows 的 C CMake 工具 测试工具核心功能 - 生成…...

蓝桥杯真题05
重新排序 问题描述 给定一个数组 A 和一些查询 Li,Ri 求数组中第 Li 至第 Ri个元素之和。 小蓝觉得这个问题很无聊, 于是他想重新排列一下数组, 使得最终每个查询结果的和尽可能地大。小蓝想知道相比原数组, 所有查询结果的总和最多可以增加多少? 输入格式 输入第一行包含…...
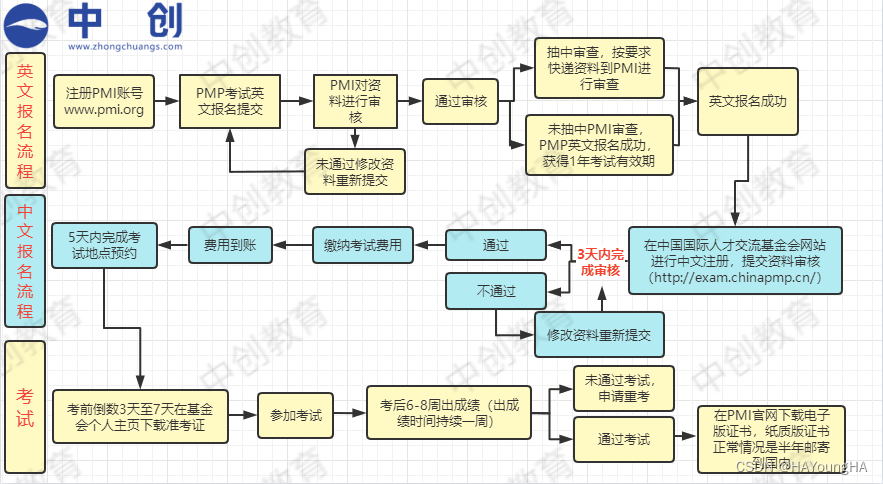
PMP那些事儿,备考小白看过来
一、PMP是什么? PMP指的是项目管理专业人士资格认证。它是由美国项目管理协会(Project Management Institute(PMI)发起的,严格评估项目管理人员知识技能是否具有高品质的资格认证考试。 其目的是为了给项目管理人员提供统一的行业标准。目前࿰…...
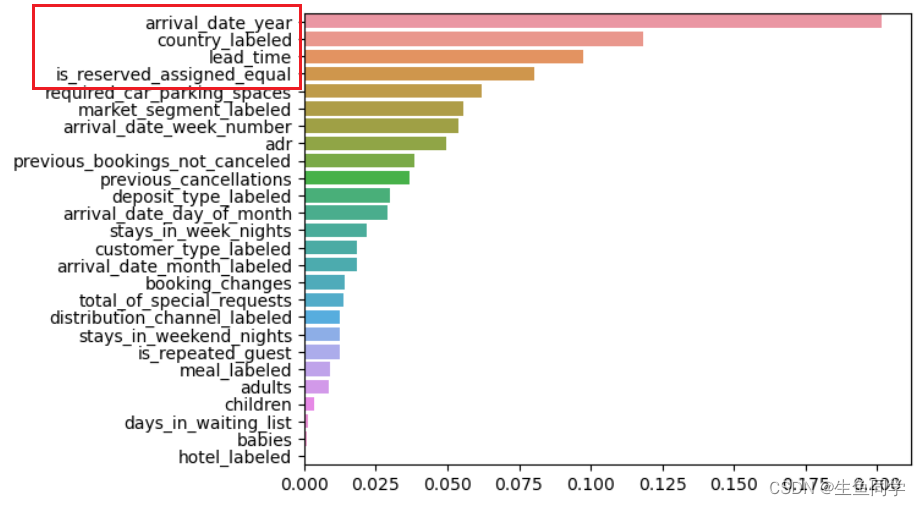
【数据分析实战】基于python对酒店预订需求进行分析
文章目录📚引言📖数据加载以及基本观察📑缺失值观察及处理🔖缺失值观察以及可视化🔖缺失值处理📖用户数据探索📑什么时间预定酒店将会更经济实惠?📑哪个月份的酒店预订是…...

【新2023Q2模拟题JAVA】华为OD机试 - 数组的中心位置
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:数组的中心位置 题目 给你一…...

Vue的props组件详解
const props defineProps({name: String, }); String 是在 defineProps() 函数中用来声明 name prop 的类型,表示 name 必须是字符串类型。如果父组件没有传入 name 或传入的 name 不是字符串类型,那么就会产生类型验证错误。 defineProps() 函数支持…...
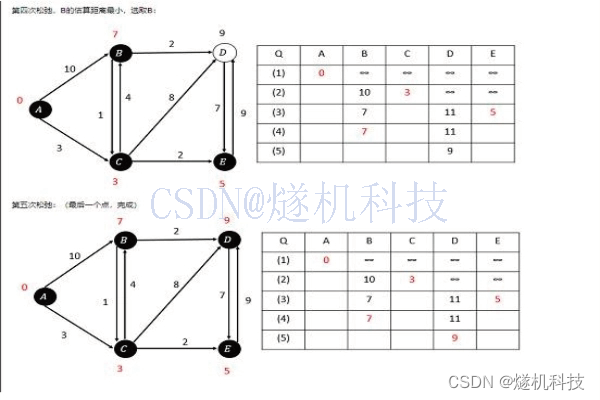
抽烟行为识别预警系统 yolov5
抽烟行为识别预警系统基于yolov5网络模型智能分析技术,抽烟行为识别预警算法通过监测现场人员抽烟行为自动存档进行报警提示。我们选择当下YOLO卷积神经网络YOLOv5来进行抽烟识别检测。6月9日,Ultralytics公司开源了YOLOv5,离上一次YOLOv4发布…...

【0基础学爬虫】爬虫基础之文件存储
大数据时代,各行各业对数据采集的需求日益增多,网络爬虫的运用也更为广泛,越来越多的人开始学习网络爬虫这项技术,K哥爬虫此前已经推出不少爬虫进阶、逆向相关文章,为实现从易到难全方位覆盖,特设【0基础学…...

airflow源码分析-任务调度器实现分析
Airflow源码分析-任务调度器实现分析 概述 本文介绍Airflow执行器的总体实现流程。通过函数调用的方式说明了Airflow scheduler的实现原理,对整个调度过程的源码进行了分析。 通过本文,可以基本把握住Airflow的调度器的运行原理主线。 启动调度器 可…...
和reduceRight())
一文学会数组的reduce()和reduceRight()
reduce()方法和reduceRight()方法依次处理数组的每个成员,最终累计为一个值。 它们的差别是,reduce()是从左到右处理,reduceRight()则是从右到左,其他完全一样。 [1, 2, 3, 4, 5].reduce(function (a, b) {console.log(a, b);ret…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...
