数据结构---二叉树
专栏:数据结构
个人主页:HaiFan.
专栏简介:这里是HaiFan.的数据结构专栏,今天的内容是二叉树。
二叉树
- 树的概念及结构
- 二叉树概念及结构
- 二叉树的概念
- 二叉树的存储结构
- 二叉树的顺序结构及实现
- 大根堆和小根堆
- 堆的实现及其各个接口
- 堆的初始化和空间销毁
- 入堆
- 删除堆顶元素
- 返回堆顶元素
- 返回堆的大小
- 判断堆是否为空
- 二叉树的链式实现
- 二叉树的初始化
- 二叉树的创建
- 前序遍历
- 中序遍历
- 后序遍历
- 二叉树的销毁
- 二叉树的大小
- 二叉树第k层的大小
- 二叉树查找数据
树的概念及结构
树是一种非线性的数据结构,是由n个有限结点组成的具有一个层次关系的集合,把称为树是因为把它倒着看很像一颗树。
- 有一个特殊的结点,称为根节点,根节点没有前驱结点
- 除根结点之后,其余的结点都是互不相交的集合,每一个集合都是一颗结构与树类似的子树。
- 树是递归定义的
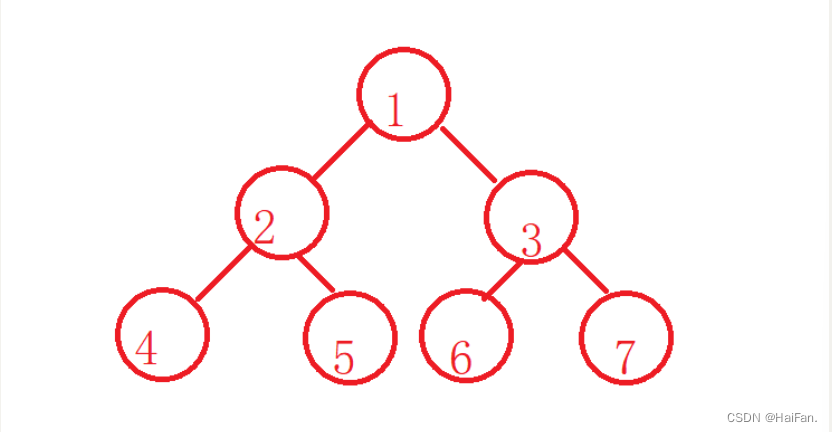
像这样,就被称为树。
子树一旦相交,就不再叫做树,而是另一种特殊的数据结构—图
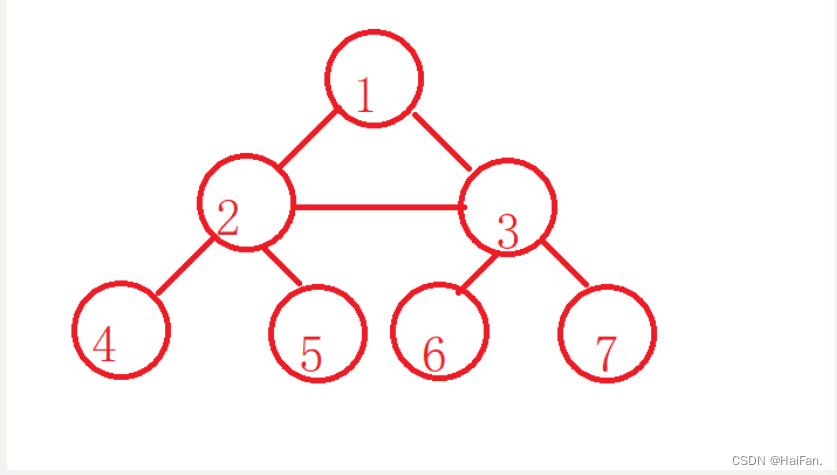
除此之外,树还有一些性质。
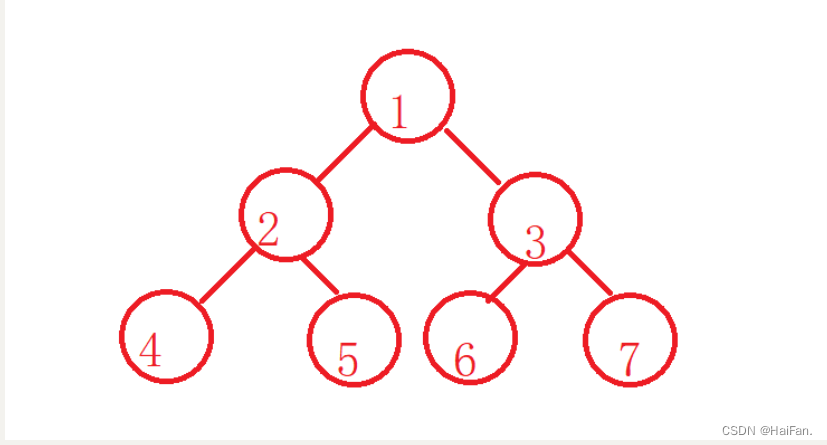
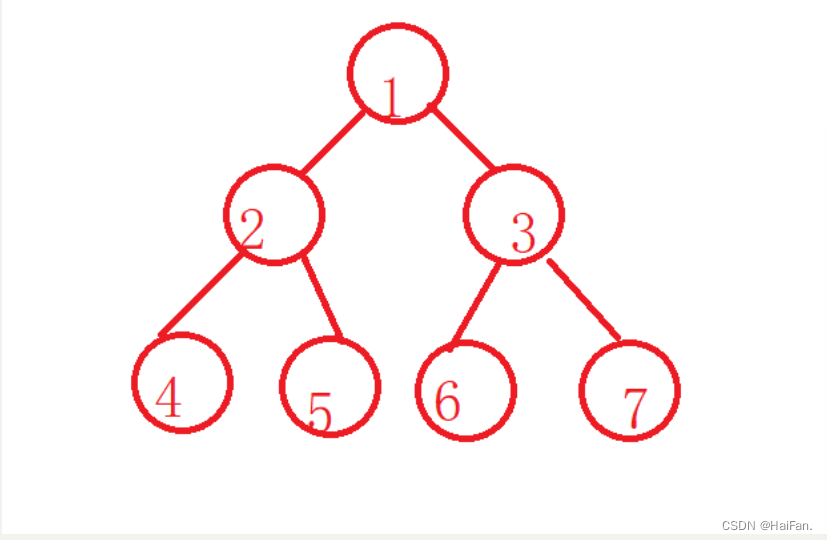
节点的度:一个节点含有的子树的个数称为该节点的度,如1的度为2
叶节点或终端节点:度为0的节点称为叶节点,如4,5,6,7都是叶节点
非终端节点或分支节点:度不为0的节点 ,如1,2,3
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点 ,如1是2的父节点
孩子节点或子节点:一个节点含有的子树的根节点,如2是1的孩子节点
兄弟结点:具有同一个父节点的子树,如2和3就互为兄弟结点
树的度:树最大的节点的度称为树的度,如树的度为2
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为3
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:4和6
节点的祖先:从根到该节点所经分支上的所有节点;如上图:1是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是1的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
那么树是怎么表示的呢?
树的结构就有点复杂了,用线性表定义树的话呢,会面临一个问题:就是一个节点可能有n个子树,那么定义多少个接口来存储该节点和子树的关系呢?这个不太好解决。于是,有大佬相出了解决办法:孩子兄弟表示法,孩子表示法等等,在这里讲解一下孩子兄弟表示法。
struct Node
{struct Node* left_child; //左孩子struct Node* right_child;//右兄弟int data;//数据
}
就比如上图中的树,
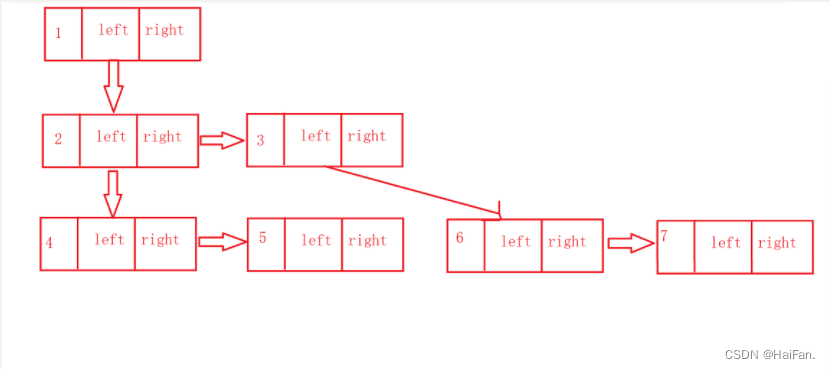
这样存,不管有多少个子树,都可以存储,left存左二子,right存兄弟。
二叉树概念及结构
二叉树的概念
二叉树是一种特殊的树形结构,它有一个根节点以及每个节点最多有两个子节点(一个左孩子,一个右孩子)
性质:
- 因为每个节点最多两个孩子,所以二叉树的最大的度不超过2
- 左儿子是左儿子,右儿子是右儿子,有顺序之分
- 叶子节点没有子节点
- 每一层上的节点数目都不超过2的n - 1次方,根节点为第一层
- 对于深度为k的二叉树来说,最多有2的n次方-1个节点,最少有k个节点
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2,则有n0 = n2 + 1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度**,**h= log(n + 1). (ps: 是log以2为底,n+1为对数)
特殊的二叉树
满二叉树:深度为k且有2的k次方-1个节点的二叉树称为满二叉树
完全二叉树:对于深度为k的二叉树来说,除了第k层节点从左到右连续排列外,其余层节点都连续的排列
二叉树的存储结构
提到存储结构,肯定是顺序结构和链式结构。
-
二叉树的顺序结构就是利用数组去存储,一般使用数组只适合完全二叉树,因为不是完全二叉树会有空间的浪费(完全二叉树会使得数组中的每一个位置都存的有元素,而非完全二叉树会造成空间的浪费,想一想为什么)
-
链式存储:定义一个结构体,结构体中 有两个结构体指针,一个存数据,一个指针用来指向左二子,一个指针用来指向右儿子。
typedef char TreeDataType; typedef struct BinaryTreeNode {TreeDataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right; }BTNode;
二叉树的顺序结构及实现
普通的二叉树不适合用数组来存储数据,因为可能会造成大量的空间浪费,而完全二叉树比较适合使用顺序结构存储。
提到完全二叉树,就不得不提到堆这一概念,堆是一个数据结构而不是管理内存的一块区域分段。
大根堆和小根堆
大根堆就是每个节点的值都大于等于父节点的值,根节点的值最大
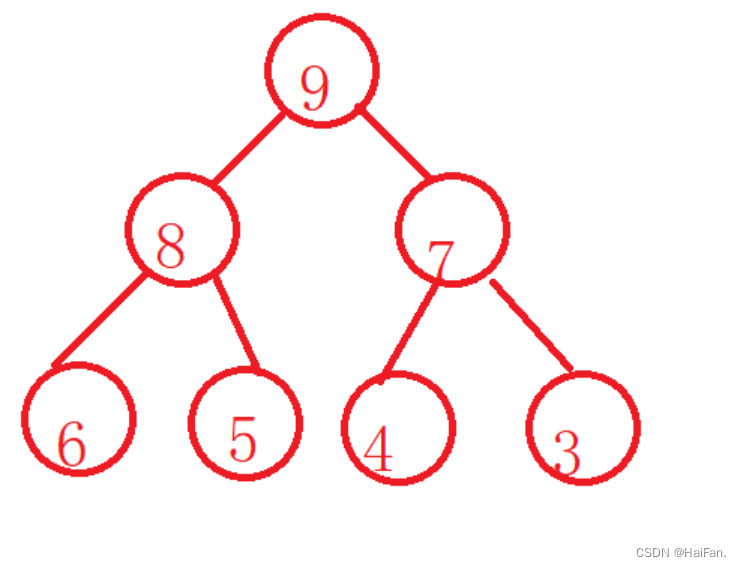
小根堆就是每个节点的值都小于等于父节点的值,根节点的值最小
堆的实现及其各个接口
实现堆,还是结构体那一套。
typedef struct Heap
{int capacity;HeapDataType* val;int count;
}Heap;void HeapInit(Heap* ps);//初始化
void HeapDestory(Heap* ps);//销毁空间void HeapPush(Heap* ps, HeapDataType x);//入堆
void HeapPop(Heap* ps);//出堆HeapDataType HeapTop(Heap* ps);//返回堆顶元素int HeapSize(Heap* ps);//堆的大小
bool HeapEmpty(Heap* ps);//堆是否为空
堆的初始化和空间销毁
之前的链表,顺序表,双链表等数据结构会的话相信堆的初始化和销毁难不倒各位。
void HeapInit(Heap* ps)
{ps->capacity = 4;ps->count = 0;ps->val = (HeapDataType*)malloc(sizeof(HeapDataType) * ps->capacity);
}void HeapDestory(Heap* ps)
{ps->capacity = ps->count = 0;free(ps->val);ps->val = NULL;
}
入堆
入堆之前要检查数组的空间是否够用,够用则直接加入数据,不够则扩容。
void HeapPush(Heap* ps, HeapDataType x)
{assert(ps);if (ps->capacity == ps->count){ps->capacity *= 2;HeapDataType* tmp = (HeapDataType*)realloc(ps->val, sizeof(HeapDataType) * ps->capacity);if (tmp == NULL){perror("malloc fail");exit(-1);}}ps->val[ps->count++] = x;HeapJustUp(ps->val, ps->count);
}但是光加入数据可不行,要进行向上调整,把数据调整成小根堆或者大根堆,但是调整是有前提的,左右子树必须是一个堆,才不会导致堆内数据乱。所以我们每加入一个数据调整一次,即可做到堆是一个大堆或者小堆。
void HeapJustUp(HeapDataType* a, int n)
{int parent = n - 2 >> 1;int child = n - 1;while (parent >= 0){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[parent] < a[child]){std::swap(a[parent], a[child]);child = parent;parent = child - 1 >> 1;}else{break;}}}
向上调整堆,要找到父亲和孩子,父亲就是元素的总个数-2之后在/2,孩子就是元素总个数-1.
因为是向上调整,父亲节点的下标会慢慢变小,所以循环条件可以设置成parent>=0,有了循环条件,还要比较左右孩子哪个大,然后在让孩子和父亲比较,最后更新父亲下标和孩子下标即可。
删除堆顶元素
删除堆顶元素就是让堆顶元素和堆底元素进行一个交换,然后元素个数-1.交换完成之后,要进行向下调整,向下调整要求左右子树是大根堆或者小根堆,在入堆这一步,我们已经完成了这个操作,所以可以直接调整。
void HeapPop(Heap* ps)
{assert(ps);assert(ps->count);std::swap(ps->val[0], ps->val[ps->count--]);HeapJustDown(ps->val, 0, ps->count);
}
那么向下调整是怎么调的呢?
因为要把堆顶元素调到下面,所以从下标为0的位置开始向下调整。
0的位置就是父亲节点,然后要找到儿子节点child = parent * 2 + 1,然后判断左右孩子哪个大,在判断父亲节点和孩子节点的大小关系,更新下标即可。
void HeapJustDown(HeapDataType* a, int parent, int n)
{int child = parent * 2 + 1;while (child <= n){if (child + 1 < n && a[child] < a[child + 1]){child++;}if (a[parent] < a[child]){std::swap(a[parent], a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
返回堆顶元素
HeapDataType HeapTop(Heap* ps)
{assert(ps);return ps->val[0];
}返回堆的大小
int HeapSize(Heap* ps)
{assert(ps);return ps->count;
}判断堆是否为空
bool HeapEmpty(Heap* ps)
{assert(ps);return ps->count == 0;
}
二叉树的链式实现
typedef char TreeDataType;typedef struct BinaryTreeNode
{TreeDataType val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* TreeInit();//初始化BTNode* BinaryTreeCreate();//创建二叉树void BinaryTreeDestory(BTNode* root);//销毁二叉树int BinaryTreeSize(BTNode* root);//二叉树的大小int BinaryTreeLeveKSize(BTNode* root, int k);//第k层有多少个元素BTNode* BinaryTreeFind(BTNode* root, TreeDataType x);//查找数据void PrevOrder(BTNode* root);//前序遍历void InOrder(BTNode* root);//中序遍历void PosOrder(BTNode* root);//后序遍历
二叉树的初始化
BTNode* TreeInit()
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = 0;root->left = NULL;root->right = NULL;return root;
}
二叉树的创建
BTNode* Creat(BTNode* t)
{TreeDataType ch;cin >> ch;if (ch == '-1'){t = NULL;}else{t->val = ch;Creat(t->left);Creat(t->right);}
}
----------------------------------------------------------BTNode* BuyNode(TreeDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* BinaryTreeCreate()
{BTNode* newnode1 = BuyNode('A');BTNode* newnode2 = BuyNode('B');BTNode* newnode3 = BuyNode('C');BTNode* newnode4 = BuyNode('D');BTNode* newnode5 = BuyNode('E');BTNode* newnode6 = BuyNode('F');BTNode* newnode7 = BuyNode('G');newnode1->left = newnode2;newnode1->right = newnode3;newnode2->left = newnode4;newnode4->left = newnode7;newnode3->left = newnode5;newnode3->right = newnode6;return newnode1;
}
两种方法创建二叉树,第一种方法是用前序遍历的方法创建二叉树,第二种是自己手动创建一个二叉树。
前序遍历
二叉树的前序遍历是先访问根节点,在访问左子树,在访问右子树,是以递归的形式进行的
void PrevOrder(BTNode* root)
{if (root == NULL){cout << "NULL ";return;}cout << root->val << ' ';PrevOrder(root->left);PrevOrder(root->right);
}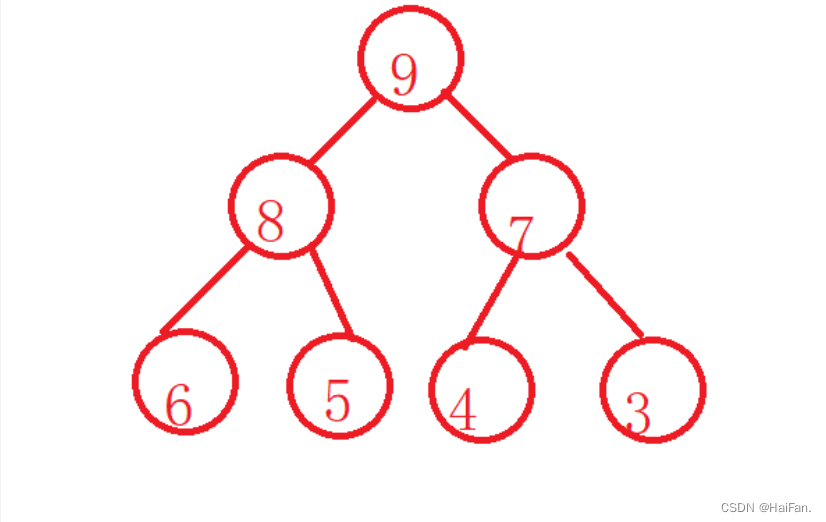
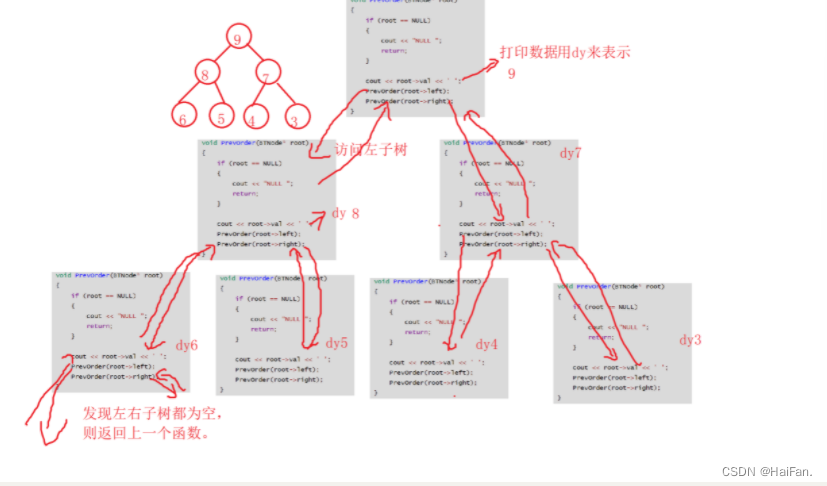
中序遍历
二叉树的中序遍历是先访问左子树,在访问根节点,然后右子树,同样是以递归的形式进行的。
void PrevOrder(BTNode* root)
{if (root == NULL){cout << "NULL ";return;}cout << root->val << ' ';PrevOrder(root->left);PrevOrder(root->right);
}
后序遍历
先左子树,在右子树,最后根节点
void InOrder(BTNode* root)
{if (root == NULL){cout << "NULL ";return;}InOrder(root->left);cout << root->val << ' ';InOrder(root->right);
}
二叉树的销毁
二叉树的创建是用的先序遍历,而二叉树的销毁则用的是后续遍历
void BinaryTreeDestory(BTNode* root)
{if (!root){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}
二叉树的大小
二叉树的大小很好判断,想一想一个树很深,很多叶子,每个子树上都有一个小领导,小领导来查他管理的地区的叶子,然后层层向上汇报,直到汇报给最大的领导,就可以完成了。
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}int l = BinaryTreeSize(root->left);int r = BinaryTreeSize(root->right);return l + r + 1;}
二叉树第k层的大小
第k层的大小该怎么判断呢,还是用上面的办法,找到第k层的小领导,让他把第k层的情况汇报给你即可
int BinaryTreeLeveKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}int l = BinaryTreeLeveKSize(root->left, k - 1);int r = BinaryTreeLeveKSize(root->right, k - 1);return l + r;}
二叉树查找数据
查找数据,从左子树找,从右子树找,依次递归即可
BTNode* BinaryTreeFind(BTNode* root, TreeDataType x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}BTNode* l = BinaryTreeFind(root->left, x);if (l){return l;}BTNode* r = BinaryTreeFind(root->right, x);if (r){return r;}return NULL;}
相关文章:

数据结构---二叉树
专栏:数据结构 个人主页:HaiFan. 专栏简介:这里是HaiFan.的数据结构专栏,今天的内容是二叉树。 二叉树树的概念及结构二叉树概念及结构二叉树的概念二叉树的存储结构二叉树的顺序结构及实现大根堆和小根堆堆的实现及其各个接口堆的…...

CMake——从入门到百公里加速6.7s
目录 一、前言 二、HelloWorld 三、CMAKE 界面 3.1 gui正则表达式 3.2 GUI构建 四 关键字 4.1 add_library 4.2 add_subdirectory 4.3 add_executable 4.4 aux_source_directory 4.5 SET设置变量 4.6 INSTALL安装 4.7 ADD_LIBRARY 4.8 SET_TARGET_PROPERTIES 4.9…...
无公网IP,在外公网远程访问RabbitMQ服务「内网穿透」
文章目录前言1.安装erlang 语言2.安装rabbitMQ3. 内网穿透3.1 安装cpolar内网穿透(支持一键自动安装脚本)3.2 创建HTTP隧道4. 公网远程连接5.固定公网TCP地址5.1 保留一个固定的公网TCP端口地址5.2 配置固定公网TCP端口地址前言 RabbitMQ是一个在 AMQP(高级消息队列协议)基础上…...

Node【二】NPM
文章目录🌟前言🌟NPM使用🌟NPM使用场景🌟NPM的常用命令🌟NPM命令使用介绍🌟 使用NPM安装模块🌟 下载三方包🌟 全局安装VS本地安装🌟 本地安装🌟 全局安装&…...
【2023最新】超详细图文保姆级教程:App开发新手入门(2)
上章节我们已经成功的创建了一个 App 项目,接下来我们讲述一下,如何导入项目、编辑代码和提交项目代码。 Let’s Go! 4. 项目导入 当用户创建一个新的应用时,YonStudio 开发工具会自动导入模板项目的默认代码,不需要手动进行代…...

sftp使用
Client端使用Server端的账户username,sftp登录Server,除了IP地址,也可以使用/etc/hosts定义的域名,注意,Client的默认路径:Shell中的当前路径,Server的默认路径:server账户家目录 …...

FastGithub---------不再为访问github苦恼
声明:只解决github加速神器,解决github打不开、用户头像无法加载、releases无法上传下载、git-clone、git-pull、git-push失败等问题。 github为什么打不开? 其实不用加速的情况下,使用5G是可以打开的,只是资源加载…...

Spring Boot AOP @Pointcut拦截注解的表达式与运算符
项目场景: 这里主要说下Spring Boot AOP中Pointcut拦截类上面的注解与方法上面的注解,怎么写表达式怎么,还有Pointcut中使用运算符。 PointCut 表达式 拦截注解的表达式有3种:annotation、within、target 1、annotation 匹配有…...

2023年第十四届蓝桥杯javaB组省赛真题
👨💻作者简介:练习时长两年半的java博主 📖个人主页:君临๑ 🎞️文章介绍:2023年第十四届蓝桥杯javaB组省赛真题 🎉所属专栏:算法专栏 🎁 ps:点…...

CefSharp.WinForms 112.2.70最新版体验
一、准备 下载最新包及依赖包(对应.NET4.5.2,后续版本可能4.6.2+)到packages中,本地升级更快 NuGet Gallery | CefSharp.WinForms 112.2.70 NuGet Gallery | CefSharp.Common 112.2.70 NuGet Gallery | cef.redist.x64 112.2.7 NuGet Gallery | cef.redist.x86 112.2.…...

leetcode每日一题:数组篇(1/2)
😚一个不甘平凡的普通人,日更算法学习和打卡,期待您的关注和认可,陪您一起学习打卡!!!😘😘😘 🤗专栏:每日算法学习 💬个人…...

每个企业经营者都应该了解的几个网络安全趋势
每个企业主都应了解的一些网络安全趋势: 1. 对实时数据可见性的需求增加 根据 IBM 发布的调查数据,企业发现并遏制漏洞的平均时间为 277 天。这种漏洞得不到解决的时间越长,泄露的数据就越多。这反过来会对您的业务产生更大的影响。企业需要…...

IDEA操作MongoDB快速上手开发
写在前面:最近在公司实习,需要完成一个实习任务。这个任务用的是SSH框架,数据库需要使用mongoDB完成。由于刚接触MongoDB,所以不是很熟练,在网上查找了大量的资料,许多都是抄来抄去的,运行一堆错误。如今&a…...

从FPGA说起的深度学习(六)-任务并行性
这是新的系列教程,在本教程中,我们将介绍使用 FPGA 实现深度学习的技术,深度学习是近年来人工智能领域的热门话题。在本教程中,旨在加深对深度学习和 FPGA 的理解。用 C/C 编写深度学习推理代码高级综合 (HLS) 将 C/C 代码转换为硬…...
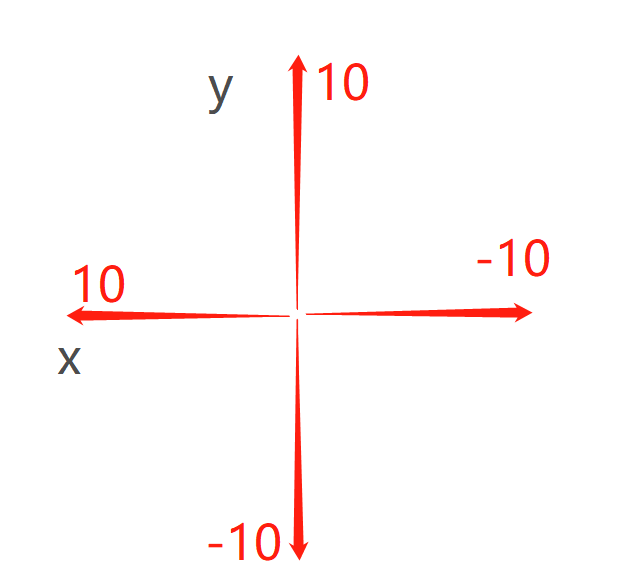
5.39 综合案例2.0 - STM32蓝牙遥控小车4(体感控制)
综合案例2.0 - 蓝牙遥控小车4- 体感控制成品展示案例说明器件说明小车连线小车源码遥控手柄遥控器连线遥控器代码1.摇杆PS2模块说明2.六轴MPU-6050说明成品展示 案例说明 用STM32单片机做了一辆蓝牙控制的麦轮小车,分享一下小车的原理和制作过程。 控制部分分为手机…...
Scala之面向对象
目录 Scala包: 基础语法: Scala包的三大作用: 包名的命名规范: 写包的好处: 包对象: 导包说明: 类和对象: 定义类: 封装: 构造器: 主从…...
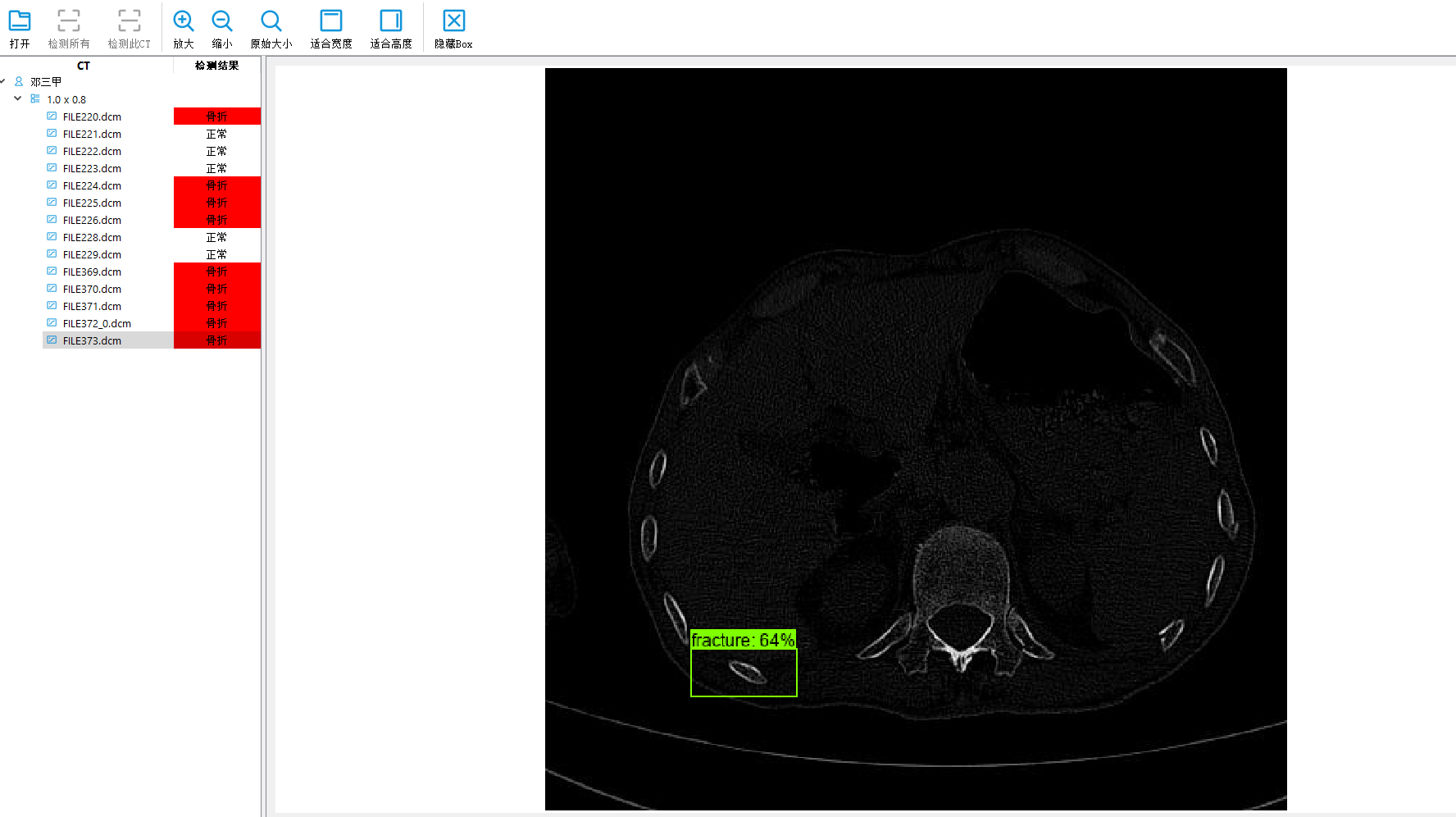
深度学习目标检测项目实战(四)—基于Tensorflow object detection API的骨折目标检测及其界面运行
深度学习目标检测项目实战(四)—基于Tensorflow object detection API的骨折目标检测及其界面运行 使用tensorflow object detection进行训练检测 参考原始代码:https://github.com/tensorflow/models/tree/master/research 我用的是1.x的版本 所以环境必须有gpu版…...

嵌入式工程师如何快速的阅读datasheet的方法
目录 ▎从项目角度来看datasheet ▎各取所需 ▎最后 Datasheet(数据手册)的快速阅读能力,是每个工程师都应该具备的基本素养。 无论是项目开始阶段的选型还是后续的软硬件设计,到后期的项目调试,经常有工程师对着英…...
合约广告)
(三)合约广告
1. 广告位(CPT)合约 系统:广告排期系统 网站把某一个广告位卖给广告商,这段时间归广告商所有,到点了下线 (1)流量选择的维度:时间段、地域等 (2)典型场景…...
【Android -- 软技能】分享一个学习方法
前言 很多人都想通过学习来提升自己,但是,可能因为两个问题,阻碍了自己的高效提升: 学什么? 怎么学? 本文将从自己的学习实践出发,针对这两个问题,给出自己的一套学习流程。 1…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
