2023年第十四届蓝桥杯javaB组省赛真题
👨💻作者简介:练习时长两年半的java博主
📖个人主页:君临๑
🎞️文章介绍:2023年第十四届蓝桥杯javaB组省赛真题
🎉所属专栏:算法专栏
🎁 ps:点赞是免费的,却可以让写博客的作者开心好几天😎
文章目录
第十四届蓝桥杯大赛软件赛省赛
试题 A: 阶乘求和【填空题】
试题 B: 幸运数字【填空题】
试题 C: 数组分割
试题 D: 矩形总面积
试题 E: 蜗牛
试题 F: 合并区域
试题 G: 买二赠一
试题 H: 合并石子
试题 I: 最大开支
试题 J: 魔法阵

第十四届蓝桥杯大赛软件赛省赛(总分:150分)
试题 A: 阶乘求和【填空题】
本题总分:5 分【问题描述】
令 S = 1! + 2! + 3! + ... + 202320232023!,求 S 的末尾 9 位数字。 提示:答案首位不为 0。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
利用java的BigInteger求 S = 1! + 2! + 3! + ... + 200!的末尾 9 位数字。
试题 B: 幸运数字【填空题】
本题总分:5 分【问题描述】
哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数,因为 (126)10 mod (1+2+6) = 0;126也是八进制下的哈沙德数,因为 (126)10 = (176)8,(126)10 mod (1 + 7 + 6) = 0; 同时 126 也是 16 进制下的哈沙德数,因为 (126)10 = (7e)16,(126)10 mod (7 + e) = 0。小蓝认为,如果一个整数在二进制、八进制、十进制、十六进制下均为哈沙德数,那么这个数字就是幸运数字,第 1 至第 10 个幸运数字的十进制表示 为:1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数字是多少?你只需要告诉小蓝这个整数的十进制表示即可。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:
暴力枚举
试题 C: 数组分割
时间限制: 1.0s 内存限制: 512.0MB 本题总分:10 分【问题描述】
小蓝有一个长度为 N 的数组 A = [A0, A1, . . . , AN−1]。现在小蓝想要从 A 对应的数组下标所构成的集合 I = {0, 1, 2, . . . , N − 1} 中找出一个子集 R1,那么R1在I 中的补集为R2。记 S1 = ∑r∈R1 Ar,S2 = ∑r∈R2 Ar,我们要求 S1 和 S2 均为偶数,请问在这种情况下共有多少种不同的 R1。当 R1 或 R2 为空集时我们将 S1 或 S2 视为0。
【输入格式】
第一行一个整数T,表示有T 组数据。 接下来输入T 组数据,每组数据包含两行:第一行一个整数 N,表示数组A 的长度;第二行输入N 个整数从左至右依次为 A0, A1, . . . , AN−1,相邻元素之间用空格分隔。
【输出格式】
对于每组数据,输出一行,包含一个整数表示答案,答案可能会很大,你需要将答案对 1000000007 进行取模后输出。
【样例输入】
2
2
6 6
2
1 6
【样例输出】
4
0
【样例说明】
对于第一组数据,答案为 4。(注意:大括号内的数字表示元素在数组中的下标。)
R1 = {0}, R2 = {1};此时 S1 = A0 = 6 为偶数, S2 = A1 = 6 为偶数。
R1 = {1}, R2 = {0};此时 S1 = A1 = 6 为偶数, S2 = A0 = 6 为偶数。
R1 = {0, 1}, R2 = {};此时 S1 = A0 + A1 = 12 为偶数, S 2 = 0 为偶数。
R1 = {}, R2 = {0, 1};此时 S1 = 0 为偶数, S2 = A0 + A1 = 12 为偶数。
对于第二组数据,无论怎么选择,都不满足条件,所以答案为 0。
【评测用例规模与约定】
对于 20% 的评测用例,1 ≤ N ≤ 10。
对于 40% 的评测用例,1 ≤ N ≤
。
对于 100% 的评测用例,1 ≤ T ≤ 10, 1 ≤ N ≤
, 0 ≤ Ai ≤
。
思路:
暴力枚举
试题 D: 矩形总面积
时间限制: 1.0s 内存限制: 512.0MB 本题总分:10 分【问题描述】
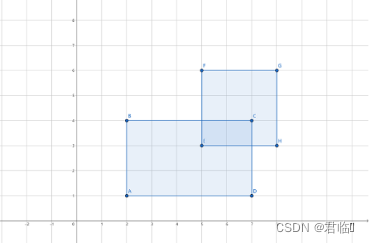
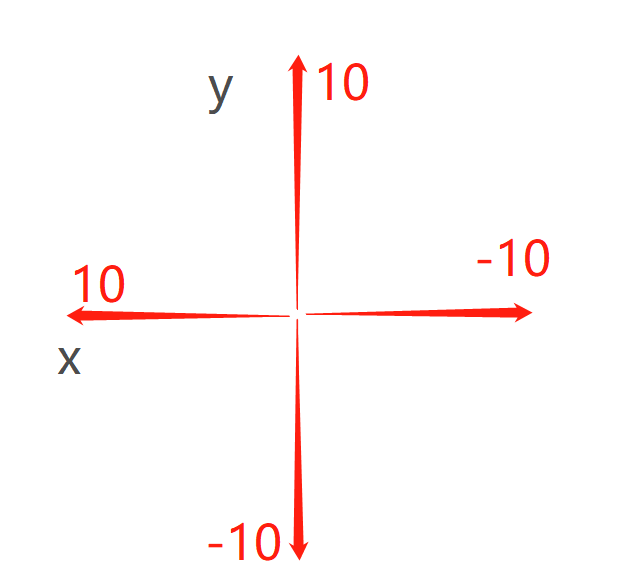
平面上有个两个矩形 R1 和 R2,它们各边都与坐标轴平行。设 (x1, y1) 和(x2, y2) 依次是 R1 的左下角和右上角坐标,(x3, y3) 和 (x4, y4) 依次是 R2 的左下角和右上角坐标,请你计算 R1和R2的总面积是多少?
注意:如果 R1 和 R2 有重叠区域,重叠区域的面积只计算一次。
【输入格式】
输入只有一行,包含 8 个整数,依次是:x1,y1,x2,y2,x3,y3,x4 和 y4。
【输出格式】
一个整数,代表答案。
【样例输入】
2 1 7 4 5 3 8 6
【样例输出】
22
【样例说明】
样例中的两个矩形如图所示:
【评测用例规模与约定】
对于 20% 的数据,R1 和 R2 没有重叠区域。
对于 20% 的数据,其中一个矩形完全在另一个矩形内部。
对于 50% 的数据,所有坐标的取值范围是 [0,
]。
对于 100% 的数据,所有坐标的取值范围是 [0,
]。
思路:
if条件判断,暴力枚举每一种情况
试题 E: 蜗牛
时间限制: 1.0s 内存限制: 512.0MB 本题总分:15 分【问题描述】
这天,一只蜗牛来到了二维坐标系的原点。 在 x 轴上长有n 根竹竿。它们平行于y 轴,底部纵坐标为 0,横坐标分别为 x1, x2, ..., xn。竹竿的高度均为无限高,宽度可忽略。蜗牛想要从原点走到第n个竹竿的底部也就是坐标 (xn, 0)。它只能在 x 轴上或者竹竿上爬行,在x 轴 上爬行速度为1 单位每秒;由于受到引力影响,蜗牛在竹竿上向上和向下爬行的速度分别为 0.7 单位每秒和 1.3 单位每秒。 为了快速到达目的地,它施展了魔法,在第 i 和 i + 1 根竹竿之间建立了传送门(0 < i < n),如果蜗牛位于第 i 根竹竿的高度为 ai 的位置 (xi , ai),就可以瞬间到达第 i + 1 根竹竿的高度为 bi+1 的位置 (xi+1, bi+1),请计算蜗牛最少需要多少秒才能到达目的地。
【输入格式】
输入共1 + n 行,第一行为一个正整数 n;
第二行为n 个正整数 x1, x2, . . . , xn;
后面 n − 1 行,每行两个正整数 ai , bi+1。
【输出格式】
输出共一行,一个浮点数表示答案(四舍五入保留两位小数)。
【样例输入】
3
1 10 11
1 1
2 1
【样例输出】
4.20
【样例说明】
蜗牛路线:(0, 0) → (1, 0) → (1, 1) → (10, 1) → (10, 0) → (11, 0),花费时间为 1 + 1/0.7 + 0 + 1/1.3 + 1 ≈ 4.20
【评测用例规模与约定】
对于 20% 的数据,保证 n ≤15.
对于 100% 的数据,保证 n ≤
,ai , bi ≤
,xi ≤
。
思路:
动态规划
试题 F: 合并区域
时间限制: 2.0s 内存限制: 512.0MB 本题总分:15 分【问题描述】
小蓝在玩一款种地游戏。现在他被分配给了两块大小均为 N × N 的正方形区域。这两块区域都按照 N × N 的规格进行了均等划分,划分成了若干块面积相同的小区域,其中每块小区域要么是岩石,要么就是土壤,在垂直或者水平方向上相邻的土壤可以组成一块土地。现在小蓝想要对这两块区域沿着边缘进行合并,他想知道合并以后可以得到的最大的一块土地的面积是多少(土地的面积就是土地中土壤小区域的块数)?在进行合并时,小区域之间必须对齐。可以在两块方形区域的任何一条边上进行合并,可以对两块方形区域进行 90 度、180 度、270 度、360 度的旋转, 但不可以进行上下或左右翻转,并且两块方形区域不可以发生重叠。
【输入格式】
第一行一个整数 N 表示区域大小。 接下来 N 行表示第一块区域,每行 N 个值为 0 或 1 的整数,相邻的整数 之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区域 是土壤。 再接下来 N 行表示第二块区域,每行 N 个值为 0 或 1 的整数,相邻的整 数之间用空格进行分隔。值为 0 表示这块小区域是岩石,值为 1 表示这块小区域是土壤。
【输出格式】
一个整数表示将两块区域合并之后可以产生的最大的土地面积。
【样例输入】
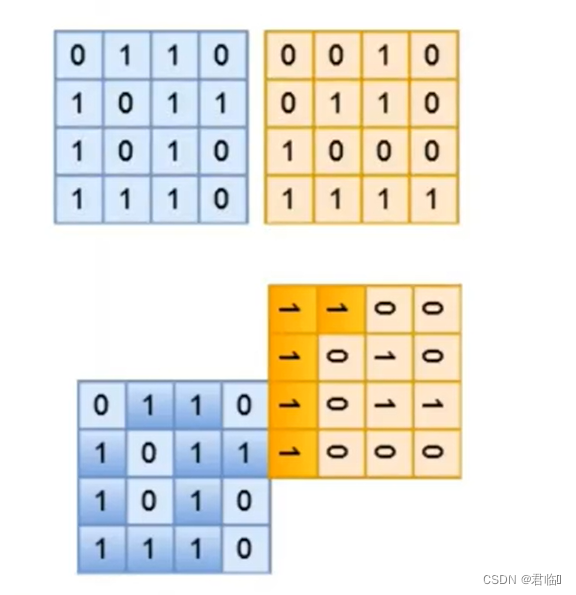
4
0 1 1 0
1 0 1 1
1 0 1 0
1 1 1 0
0 0 1 0
0 1 1 0
1 0 0 0
1 1 1 1
【样例输出】
15
【样例说明】
第一张图展示了样例中的两块区域的布局。第二张图展示了其中一种最佳 的合并方式,此时最大的土地面积为 15。
【评测用例规模与约定】
对于 30% 的数据,1 ≤ N ≤ 5。
对于 60% 的数据,1 ≤ N ≤ 15。
对于 100% 的数据,1 ≤ N ≤ 50。
思路:
DFS
下图的两种情况是坑,所以还是老老实实用dfs枚举每一种情况吧。
试题 G: 买二赠一
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分【问题描述】
某商场有 N 件商品,其中第 i 件的价格是 Ai。现在该商场正在进行 “买二 赠一” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P(如果两件商品价格一样, 则 P 等于其中一件商品的价格),就可以从剩余商品中任选一件价格不超过 P/2 的商品,免费获得这一件商品。可以通过反复购买 2 件商品来获得多件免费商品,但是每件商品只能被购买或免费获得一次。 小明想知道如果要拿下所有商品(包含购买和免费获得),至少要花费多少钱?
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数,代表 A1, A2, A3, . . . ,AN。
【输出格式】
输出一个整数,代表答案。
【样例输入】
7
1 4 2 8 5 7 1
【样例输出】
25
【样例说明】
小明可以先购买价格 4 和 8 的商品,免费获得一件价格为1 的商品;再后买价格为 5 和 7 的商品,免费获得价格为 2 的商品;最后单独购买剩下的一件价格为 1 的商品。总计花费 4 + 8 + 5 + 7 + 1 = 25。不存在花费更低的方案。
【评测用例规模与约定】
对于 30% 的数据,1 ≤ N ≤ 20。
对于 100% 的数据,1 ≤ N ≤ 5 ×
,1 ≤ Ai ≤
。
试题 H: 合并石子
时间限制: 1.0s 内存限制: 512.0MB 本题总分:20 分【问题描述】
在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色,颜色可能是颜色 0,颜色 1 或者颜色 2 中的其中一种。 现在要对石子进行合并,规定每次只能选择位置相邻并且颜色相同的两堆石子进行合并。合并后新堆的相对位置保持不变,新堆的石子数目为所选择的两堆石子数目之和,并且新堆石子的颜色也会发生循环式的变化。具体来说: 两堆颜色 0 的石子合并后的石子堆为颜色 1,两堆颜色 1 的石子合并后的石子堆为颜色 2,两堆颜色 2 的石子合并后的石子堆为颜色 0。本次合并的花费为所选择的两堆石子的数目之和。 给出 N 堆石子以及他们的初始颜色,请问最少可以将它们合并为多少堆石子?如果有多种答案,选择其中合并总花费最小的一种,合并总花费指的是在 所有的合并操作中产生的合并花费的总和。
【输入格式】
第一行一个正整数 N 表示石子堆数。 第二行包含 N 个用空格分隔的正整数,表示从左至右每一堆石子的数目。 第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。
【输出格式】
一行包含两个整数,用空格分隔。其中第一个整数表示合并后数目最少的石头堆数,第二个整数表示对应的最小花费。
【样例输入】
5
5 10 1 8 6
1 1 0 2 2
【样例输出】
2 44
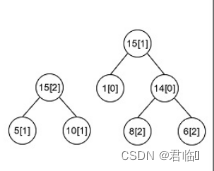
【样例说明】
上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目, 在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两 堆石子,所产生的合并总花费为 15 + 14 + 15 = 44;右图的这种合并方式最终 也剩下了两堆石子,但产生的合并总花费为 14 + 15 + 25 = 54。综上所述,我们选择合并花费为 44 的这种方式作为答案。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 10。
对于 50% 的评测用例,1 ≤ N ≤ 50。
对于 100% 的评测用例,1 ≤ N ≤ 300, 1 ≤ 每堆石子的数目 ≤ 1000。
试题 I: 最大开支
时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分【问题描述】
小蓝所在学校周边新开业了一家游乐园,小蓝作为班长,打算组织大家去游乐园玩。已知一共有 N 个人参加这次活动,游乐园有 M 个娱乐项目,每个项目都需要买门票后才可进去游玩。门票的价格并不是固定的,团购的人越多单价越便宜,当团购的人数大于某个阈值时,这些团购的人便可以免费进入项 目进行游玩。这 M 个娱乐项目是独立的,所以只有选择了同一个项目的人才可 以参与这个项目的团购。第 i 个项目的门票价格 Hi 与团购的人数 X 的关系可以看作是一个函数:
Hi(X) = max(Ki × X + Bi , 0)
max 表示取二者之中的最大值。当 Hi = 0 时说明团购人数达到了此项目的 免单阈值。 这 N 个人可以根据自己的喜好选择 M 个娱乐项目中的一种,或者有些人 对这些娱乐项目都没有兴趣,也可以选择不去任何一个项目。每个人最多只会选择一个娱乐项目,如果多个人选择了同一个娱乐项目,那么他们都将享受对应的团购价格。小蓝想知道他至少需要准备多少钱,使得无论大家如何选择, 他都有能力支付得起所有 N 个人购买娱乐项目的门票钱。
【输入格式】
第一行两个整数 N、M,分别表示参加活动的人数和娱乐项目的个数。 接下来 M 行,每行两个整数,其中第 i 行为 Ki、Bi,表示第 i 个游乐地点 的门票函数中的参数。
【输出格式】
一个整数,表示小蓝至少需要准备多少钱,使得大家无论如何选择项目, 自己都支付得起。
【样例输入】
4 2
-4 10
-2 7
【样例输出】
12
【样例说明】
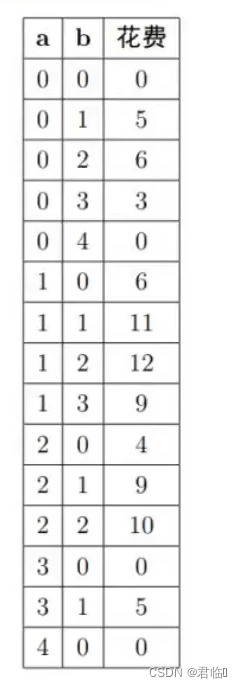
样例中有 4 个人,2 个娱乐项目,我们用一个二元组 (a, b) 表示 a 个人选择了第一个娱乐项目,b 个人选择了第二个娱乐项目,那么就有 4 − a − b 个 人没有选择任何项目,方案 (a, b) 对应的门票花费为 max(−4 × a + 10, 0) × a + max(−2 × b + 7, 0) × b,所有的可能如下所示:
思路:
贪心算法。
计算每个项目多一个人参加时造成的费用变化量,贪心的参加费用变化最多的项目。
试题 J: 魔法阵
时间限制: 1.0s 内存限制: 512.0MB 本题总分:25 分【问题描述】
魔法师小蓝为了营救自己的朋友小Q,来到了敌人布置的魔法阵。魔法阵可以看作是一幅具有 N 个结点 M 条边的无向图,结点编号为 0, 1, 2, . . . , N − 1, 图中没有重边和自环。敌人在每条边上都布置了陷阱,每条边都有一个伤害属性 w,每当小蓝经过一条边时就会受到这条边对应的 w 的伤害。小蓝从结点 0出发,沿着边行走,想要到达结点 N − 1 营救小 Q。 小蓝有一种特殊的魔法可以使用,假设一条路径按照顺序依次经过了以下L 条边:e1, e2, . . . , eL(可以出现重复的边),那么期间小蓝受到的总伤害就是P = ∑L i=1 w(ei),w(ei) 表示边 ei 的伤害属性。如果 L ≥ K,那么小蓝就可以从 这 L 条边当中选出连续出现的 K 条边 ec , ec+1, . . . , ec+K−1 并免去在这 K 条边行走期间所受到的伤害,即使用魔法之后路径总伤害变为 P ′ = P − ∑c+K−1 i = c w(ei)。 注意必须恰好选出连续出现的 K 条边,所以当 L < K 时无法使用魔法。 小蓝最多只可以使用一次上述的魔法,请问从结点 0 出发到结点 N − 1 受 到的最小伤害是多少?题目保证至少存在一条从结点 0 到 N − 1 的路径。
【输入格式】
第一行输入三个整数,N, K, M,用空格分隔。 接下来 M 行,每行包含三个整数 u, v,w,表示结点 u 与结点 v 之间存在一 条伤害属性为 w 的无向边。
【输出格式】
输出一行,包含一个整数,表示小蓝从结点 0 到结点 N − 1 受到的最小伤害。
【样例输入 1】
4 2 3
0 1 2
1 2 1
2 3 4
【样例输出 1】
2
【样例输入 2】
2 5 1
0 1 1
【样例输出 2】
0
【样例说明】
样例 1,存在路径:0 → 1 → 2 → 3,K = 2,如果在 0 → 1 → 2 上使用魔 法,那么答案就是 0 + 0 + 4 = 4;如果在 1 → 2 → 3 上使用魔法,那么答案就 是 2 + 0 + 0 = 2。再也找不到比 2 还小的答案了,所以答案就是 2。 样例 2,存在路径:0 → 1 → 0 → 1 → 0 → 1,K = 5,这条路径总计恰好 走了 5 条边,所以正好可以用魔法消除所有伤害,答案是 0。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 20。
对于 50% 的评测用例,1 ≤ N ≤ 100。
对于 100% 的评测用例,1 ≤ N ≤ 1000, 1 ≤ M ≤ N×(N−1)/2 ,1 ≤ K ≤ 10, 0 ≤ u, v ≤ N − 1,1 ≤ w ≤ 1000。
总结:
在考场上,一张卷子做下来,发现自己只会枚举这一种算法了😅,来自算法小白的蓝桥杯总结。用java代码实现解题,以后补上。
结束语
- 记录生活,分享知识!
- 本人还在不断学习中,如有问题可留言交流学习!

相关文章:

2023年第十四届蓝桥杯javaB组省赛真题
👨💻作者简介:练习时长两年半的java博主 📖个人主页:君临๑ 🎞️文章介绍:2023年第十四届蓝桥杯javaB组省赛真题 🎉所属专栏:算法专栏 🎁 ps:点…...

CefSharp.WinForms 112.2.70最新版体验
一、准备 下载最新包及依赖包(对应.NET4.5.2,后续版本可能4.6.2+)到packages中,本地升级更快 NuGet Gallery | CefSharp.WinForms 112.2.70 NuGet Gallery | CefSharp.Common 112.2.70 NuGet Gallery | cef.redist.x64 112.2.7 NuGet Gallery | cef.redist.x86 112.2.…...

leetcode每日一题:数组篇(1/2)
😚一个不甘平凡的普通人,日更算法学习和打卡,期待您的关注和认可,陪您一起学习打卡!!!😘😘😘 🤗专栏:每日算法学习 💬个人…...

每个企业经营者都应该了解的几个网络安全趋势
每个企业主都应了解的一些网络安全趋势: 1. 对实时数据可见性的需求增加 根据 IBM 发布的调查数据,企业发现并遏制漏洞的平均时间为 277 天。这种漏洞得不到解决的时间越长,泄露的数据就越多。这反过来会对您的业务产生更大的影响。企业需要…...

IDEA操作MongoDB快速上手开发
写在前面:最近在公司实习,需要完成一个实习任务。这个任务用的是SSH框架,数据库需要使用mongoDB完成。由于刚接触MongoDB,所以不是很熟练,在网上查找了大量的资料,许多都是抄来抄去的,运行一堆错误。如今&a…...

从FPGA说起的深度学习(六)-任务并行性
这是新的系列教程,在本教程中,我们将介绍使用 FPGA 实现深度学习的技术,深度学习是近年来人工智能领域的热门话题。在本教程中,旨在加深对深度学习和 FPGA 的理解。用 C/C 编写深度学习推理代码高级综合 (HLS) 将 C/C 代码转换为硬…...
5.39 综合案例2.0 - STM32蓝牙遥控小车4(体感控制)
综合案例2.0 - 蓝牙遥控小车4- 体感控制成品展示案例说明器件说明小车连线小车源码遥控手柄遥控器连线遥控器代码1.摇杆PS2模块说明2.六轴MPU-6050说明成品展示 案例说明 用STM32单片机做了一辆蓝牙控制的麦轮小车,分享一下小车的原理和制作过程。 控制部分分为手机…...
Scala之面向对象
目录 Scala包: 基础语法: Scala包的三大作用: 包名的命名规范: 写包的好处: 包对象: 导包说明: 类和对象: 定义类: 封装: 构造器: 主从…...
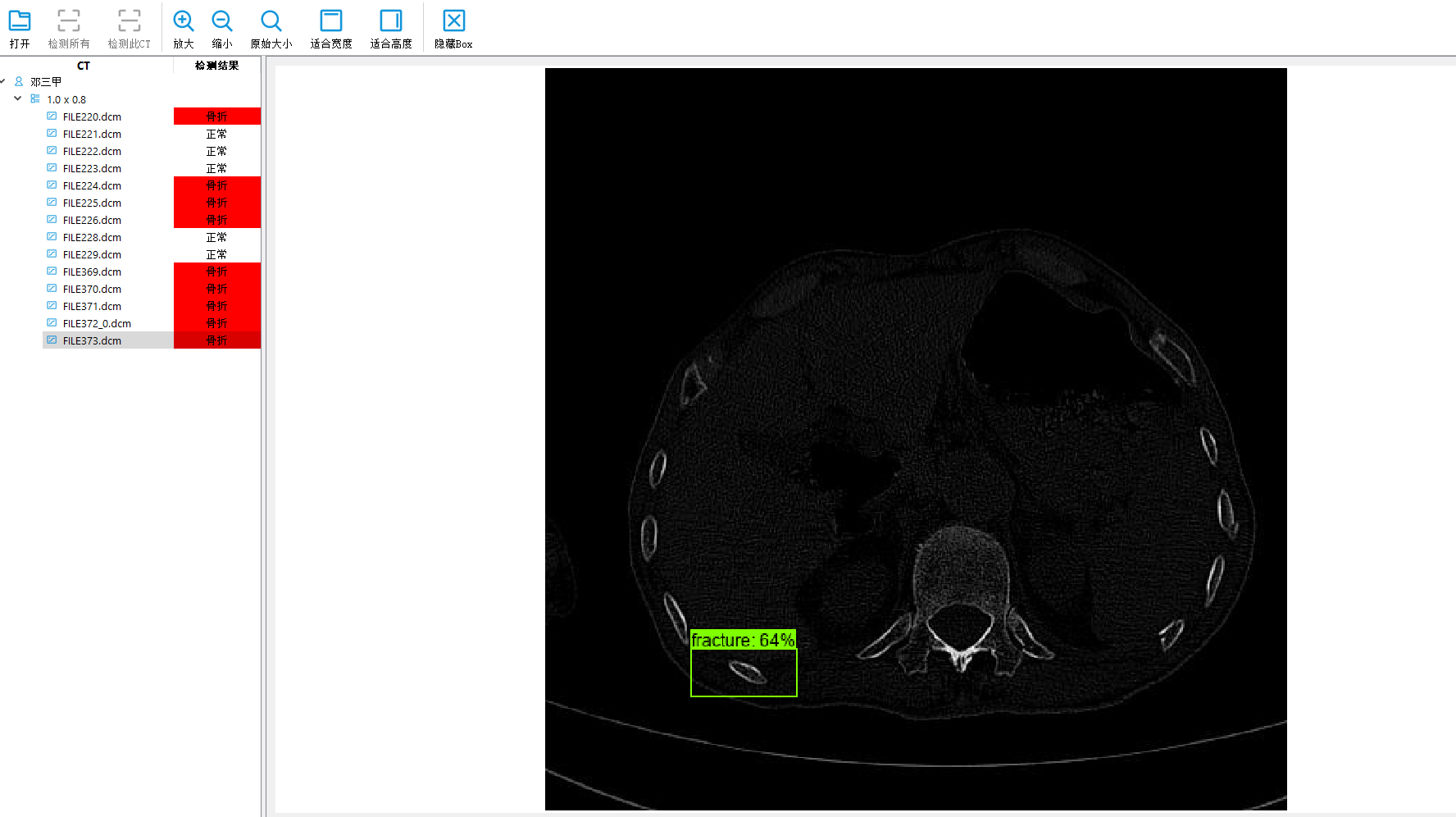
深度学习目标检测项目实战(四)—基于Tensorflow object detection API的骨折目标检测及其界面运行
深度学习目标检测项目实战(四)—基于Tensorflow object detection API的骨折目标检测及其界面运行 使用tensorflow object detection进行训练检测 参考原始代码:https://github.com/tensorflow/models/tree/master/research 我用的是1.x的版本 所以环境必须有gpu版…...

嵌入式工程师如何快速的阅读datasheet的方法
目录 ▎从项目角度来看datasheet ▎各取所需 ▎最后 Datasheet(数据手册)的快速阅读能力,是每个工程师都应该具备的基本素养。 无论是项目开始阶段的选型还是后续的软硬件设计,到后期的项目调试,经常有工程师对着英…...
合约广告)
(三)合约广告
1. 广告位(CPT)合约 系统:广告排期系统 网站把某一个广告位卖给广告商,这段时间归广告商所有,到点了下线 (1)流量选择的维度:时间段、地域等 (2)典型场景…...
【Android -- 软技能】分享一个学习方法
前言 很多人都想通过学习来提升自己,但是,可能因为两个问题,阻碍了自己的高效提升: 学什么? 怎么学? 本文将从自己的学习实践出发,针对这两个问题,给出自己的一套学习流程。 1…...
)
Python-DQN代码阅读(10)
目录 1.代码 1.1 代码阅读 1.2 代码分解 1.2.1 f open("experiments/" str(env.spec.id) "/performance.txt", "a") 1.2.2 f.write(str(ep) " " str(time_steps) " " str(episode_rewards) " " str(…...

MongoDB入坑
MongoDB入坑一、体系架构1、简介2、MongoDB VS RDBMS3、文件4、体系结构二、权限管理1、开启2、角色三、存储引擎四、备份 & 恢复五、高可用0、主从复制1、副本集2、分片一、体系架构 1、简介 DBMS No.5;NoSQL Document No.1 1)BSON BSON(Binary …...
【论文总结】针对操作系统级虚拟化的抽象资源攻击
介绍 这是一篇来自2021CCS的论文,作者有Nanzi Yang, Wenbo Shen, Jinku Li, Yutian Yang, Kangjie Lu, Jietao Xiao, Tianyu Zhou, Chenggang Qin, Wang Yu, Jianfeng Ma, Kui Ren。 概述 本文的贡献如下: 新的攻击面:作者揭示了一个影响操…...

C# 提取 PDF 文档中的文本
C# .Net 使用 IText7 从PDF文件中提取出所有文本内容 【文 / 张赐荣】 首先在 Nuget 包管理器中,安装"itext7" 和 "itext7.font-asian"。 如果不安装 "itext7.font-asian" PDF 文件中有非Unicode编码的字符,将会抛出运行时异常:iText.IO.Excep…...
mac如何升级node版本、切换node版本
一、mac如何升级node版本 当前官网稳定版本是18.15.0 所以我从v14.17.4升级到v18.15.0 二、mac如何切换node版本 切换到16.20.0版本 三、这里是用node.js的多版本管理器n来升级和切换的,命令如下: 1、sudo npm cache clean -f //清除node.js的cache …...

一位大专学历的女程序员要求月薪25K,学历重要吗?来看看面试过程
“请提供一份完整的简历,以便我审查。从您的简历中,我感觉您写得还不错。方便的话,您可以自我简单介绍一下吗?“ ”好的,我叫李娟,拥有大专学位,目前正在寻找一份Java开发架构师的工作岗位。“…...
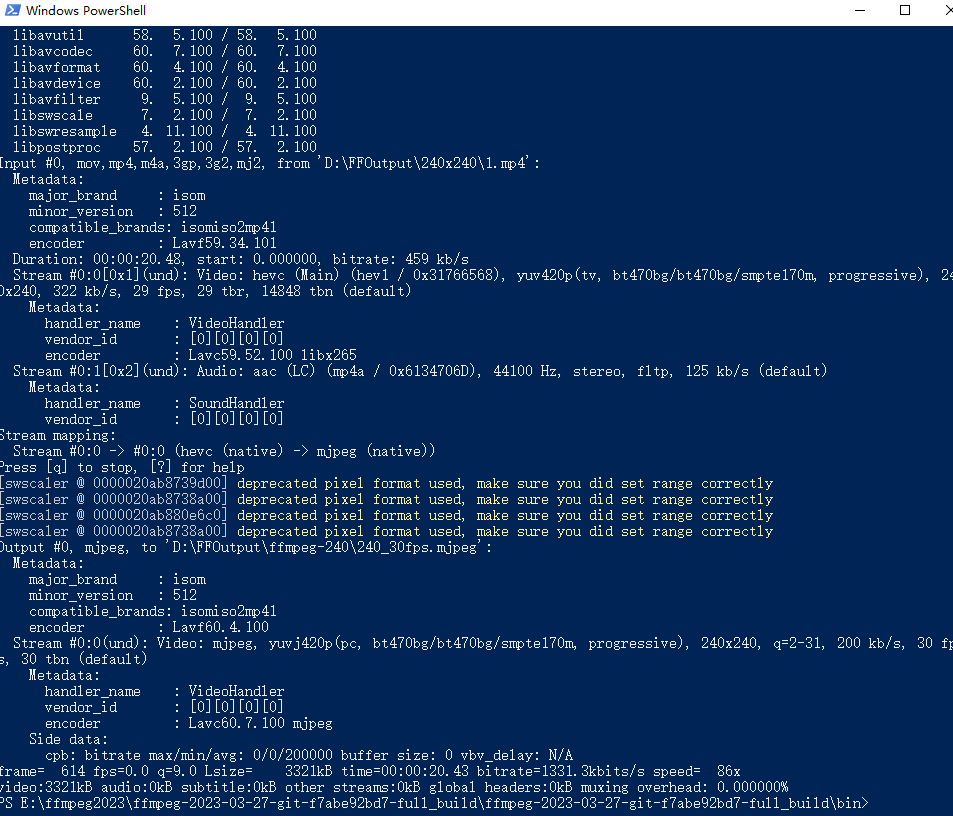
ESP32驱动1.28寸GC9A01播放视频(一、视频分辨率的调整和视频格式的转换)
ESP32驱动1.28寸GC9A01播放视频(一、视频分辨率的调整和视频格式的转换)播放前准备转换视频分辨率用FFmpeg将.MP4转换为.mjpeg格式FFmpeg的win10环境搭建FFmpeg的下载环境变量的搭建MP4转换成mjpeg格式总结播放前准备 1.28寸GC9A01屏幕的分辨率是240x24…...

epoll的LT模式(水平触发)和ET模式(边沿触发)
前言 epoll的触发模式是个引发讨论非常多的话题,网络上这方面总结的文章也很多,首先从名字上就不是很统一,LT模式常被称为水平触发、电平触发、条件触发,而ET模式常被称为边缘触发、边沿触发等,这些都是从英文翻译过来…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...